An object is released from rest. The time it takes to fall through as distance h and the speed of the object as it falls through this distance are measured with a pendulum clock. The entire apparatus is taken on the moon and the experiment is repeated
the measured times are same
the measured speeds are same
the actual times in the fall are equal
the actual speeds are equal
The correct Answer is:A, B
To solve this problem, we need to analyze the motion of an object falling under the influence of gravity on both Earth and the Moon. The key points to consider are the equations of motion, the effects of gravity, and the measurements taken.
1. Understanding Initial Conditions:
- The object is released from rest, which means its initial velocity u=0.
2. Using the Equation of Motion:
- The equation of motion that relates the final velocity v, initial velocity u, acceleration g, and distance h is given by:
v2=u2+2gh
- Since u=0, the equation simplifies to:
v2=2gh
- Therefore, the final velocity v as the object falls through distance h is:
v=√2gh
3. Calculating Time of Fall:
- The time t taken to fall through distance h can be derived from the second equation of motion:
h=ut+12gt2
- Again, since u=0, we have:
h=12gt2
- Rearranging gives:
t2=2hg⇒t=√2hg
4. Comparing Earth and Moon:
- On Earth, the acceleration due to gravity g is approximately 9.81m/s2.
- On the Moon, the acceleration due to gravity g′ is approximately 16g (or about 1.62m/s2).
- Thus, the velocity on the Moon becomes:
v′=√2g′h=√2⋅16g⋅h=√13⋅2gh=1√3√2gh
- The time taken to fall through distance h on the Moon is:
t′=√2hg′=
⎷2h16g=√12hg=2√3√hg
5. Conclusion:
- The measured times and speeds will be different on the Moon compared to Earth due to the difference in gravitational acceleration.
- Therefore, the correct options are:
- The measured times are the same (as they are measured with the same clock).
- The measured speeds are not the same.
- The actual times in the fall are not equal.
- The actual speeds are not equal.
Final Answer:
- The correct options are:
- The measured times are the same.
- The measured speeds are not the same.
- The object is released from rest, which means its initial velocity u=0.
- The equation of motion that relates the final velocity v, initial velocity u, acceleration g, and distance h is given by:
v2=u2+2gh
- Since u=0, the equation simplifies to:
v2=2gh
- Therefore, the final velocity v as the object falls through distance h is:
v=√2gh
- The time t taken to fall through distance h can be derived from the second equation of motion:
h=ut+12gt2
- Again, since u=0, we have:
h=12gt2
- Rearranging gives:
t2=2hg⇒t=√2hg
- On Earth, the acceleration due to gravity g is approximately 9.81m/s2.
- On the Moon, the acceleration due to gravity g′ is approximately 16g (or about 1.62m/s2).
- Thus, the velocity on the Moon becomes:
v′=√2g′h=√2⋅16g⋅h=√13⋅2gh=1√3√2gh
- The time taken to fall through distance h on the Moon is:
t′=√2hg′=
⎷2h16g=√12hg=2√3√hg
- The measured times and speeds will be different on the Moon compared to Earth due to the difference in gravitational acceleration.
- Therefore, the correct options are:
- The measured times are the same (as they are measured with the same clock).
- The measured speeds are not the same.
- The actual times in the fall are not equal.
- The actual speeds are not equal.
- The correct options are:
- The measured times are the same.
- The measured speeds are not the same.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective -1
21 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
Knowledge Check
An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1
A ball is dropped from the top of a tower of height (h). It covers a distance of h/2 in the last second of its motion. How long does the ball remain in air?
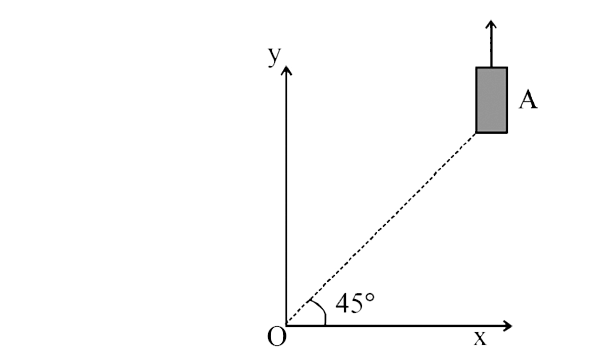
View SolutionOn a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−axis ( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x− axis , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x− axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle θ made by the velocity vector of the ball with the x−axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(3).
View SolutionA body freely falling from the rest has velocity v after it falls through a height h the distance it has to fall down for its velocity to become double is
View SolutionAn object of mass m is allowed to fall from rest along a rough inclined plane. The speed of the object on reaching the bottom of the plane is proportional to:
View SolutionAn object starts from rest from the point A to rest at point B on the same straight line at a distance d. It moves over the first part of the distance with an acceleration αm/s2 and for the remainder the retardation βm/s2. Find the time taken to complete the journey.
View SolutionAn object is dropped from rest. If it falls distance x during first second and additional distance y in next two seconds. Then ratio of xy is
View SolutionA particle is dropped from rest from a large height Assume g to be constant throughout the motion. The time taken by it to fall through successive distance of 1m each will be :
View Solution