In figure, k=100N/m,M=1kg and F=10N

(a) Find the compression of the spring in the equilibrium position
(b) A sharp blow by some external agent imparts a speed of 2m/s to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
(c) Find the time period of the resulting simple harmonic motion.
(d) Find the amplitude.
(e) Write the potential energy of the spring when the block is at the left estreme.
(f) Write the potential energy of the spring when the block is at the right extreme.
The answers of (b), (e) and (f) are different. Explain why this does not violate the principle of conservation of energy ?
The correct Answer is:A, B, C, D
Given k=100BNm,m=1kgandF=10N<br>a.Intheequilibriumposition<br>Compression =δ=Fk=10100
=0.1m=10cm
b. The below imparts a speed of 2 m/s to the block towards left.
∴+P.E.+K.E.=12kδ2+12Mv2
=12x100×(0.1)2+12x1×4
=0.5+2=2.5J
c.Timeperiod2pisqrt(M/k)<br>=2pi sqrt(M/100)=pi/5 sec<br>d.Lettheamplitudebexwhighmeansthedistasncebetwenthemeanpositionandtheextremeposition.<br>So∈theextremeposition,compressionofthespr∈gis(x-K)<br>Since∈SHMthe→tle≠rgyrema∈sconstant,<br>1/2k(x+delta)^2=1/2kdelta^2+1/2mv^2+Fx<br>=2.5+10x
[because 1/2kdelta^2+1/2mv^2=2.5]<br>so,50(x+0.1)^2=2.5+10x<br>:. 50x^2+0.5+10x=2.5+10x<br>=:. 50x^2=2<br>rarr x^2=2/50=4/100<br>rarr x=2/50x=20m<br>e.potentiale≠rgyatthe≤ftextremeisgivenby<br>P.E. =1/2k(x+delta)^2<br>=1/2x100xx(0.1+0.2)^2<br>=50xx(0.09)=4.5J<br>f.Potentiale≠rgyattherightextremeisgivenby<br>P.E. 1/2k(x+delta)^2-F(2x)<br>[2x=distancebetweentwoextreme)
=4.5−10(0.4)=0.5J
The different values is b, e, and f do not violate law of conservastion of energy as the work is done by the exterN/Al force 10 N.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
15 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
Find the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.

View SolutionThe spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find

(a) the amplitude and the time period of the motion of the block,
(b) the energy stored in the spring when the block passes through the equilibrium position and
(c) the kinetic energy of the block at this position.
View SolutionThe spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find

(a) the amplitude and the time period of the motion of the block,
(b) the energy stored in the spring when the block passes through the equilibrium position and
(c) the kinetic energy of the block at this position.
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionEach of the blocks shown in figure has mass 1 kg. The rear block moves with a speed of 2 m/s towards the front block kept at rest. The spring attached to the front block islight and has a spring constant 50 N/m. find the maximum compression of the spring.

View SolutionIn figure shown if 2 kg block is moving at an acceleration 2m/s2, find the elongationin spring and acceleration of 4 kg block at this instant. Take g= 10m/s2.
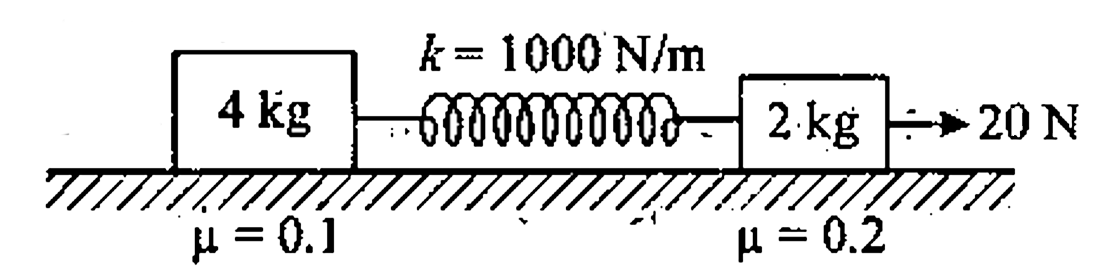
View SolutionA block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is

View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View Solution
