Show that the particle speed can never be equal to the wave speed in a sine wave if the amplitude is less than wavelength divided by 2π.
To show that the particle speed can never be equal to the wave speed in a sine wave if the amplitude is less than the wavelength divided by 2π, we can follow these steps:
Step 1: Write the wave equation
The equation for a sine wave traveling in the positive x-direction can be expressed as:
y(x,t)=Asin(ωt−kx)
where:
- A is the amplitude,
- ω is the angular frequency,
- k is the wave number,
- x is the position,
- t is the time.
Step 2: Differentiate the wave equation with respect to time
To find the particle speed, we need to differentiate the wave equation with respect to time t:
vp=∂y∂t=Aωcos(ωt−kx)
Here, vp represents the particle speed.
Step 3: Determine the maximum particle speed
The maximum particle speed occurs when cos(ωt−kx)=1:
vp,max=Aω
Step 4: Relate wave speed to wavelength and frequency
The wave speed v can be expressed in terms of wavelength λ and frequency f:
v=λf
Since f=ω2π, we can rewrite the wave speed as:
v=λω2π
Step 5: Use the condition given in the problem
We are given the condition that the amplitude A is less than λ2π:
A<λ2π
Now, substituting this into the expression for maximum particle speed:
Aω<λ2π⋅ω
Step 6: Compare maximum particle speed with wave speed
From the previous steps, we have:
vp,max<λω2π
Now, substituting λω2π with v:
vp,max<v
Conclusion
Since the maximum particle speed vp,max is less than the wave speed v, we conclude that the particle speed can never be equal to the wave speed if the amplitude A is less than λ2π.
Thus, we have shown that:
Particle speed can never equal wave speed if A<λ2π.
The equation for a sine wave traveling in the positive x-direction can be expressed as:
y(x,t)=Asin(ωt−kx)
where:
- A is the amplitude,
- ω is the angular frequency,
- k is the wave number,
- x is the position,
- t is the time.
To find the particle speed, we need to differentiate the wave equation with respect to time t:
vp=∂y∂t=Aωcos(ωt−kx)
Here, vp represents the particle speed.
The maximum particle speed occurs when cos(ωt−kx)=1:
vp,max=Aω
The wave speed v can be expressed in terms of wavelength λ and frequency f:
v=λf
Since f=ω2π, we can rewrite the wave speed as:
v=λω2π
We are given the condition that the amplitude A is less than λ2π:
A<λ2π
Now, substituting this into the expression for maximum particle speed:
Aω<λ2π⋅ω
From the previous steps, we have:
vp,max<λω2π
Now, substituting λω2π with v:
vp,max<v
Since the maximum particle speed vp,max is less than the wave speed v, we conclude that the particle speed can never be equal to the wave speed if the amplitude A is less than λ2π.
Particle speed can never equal wave speed if A<λ2π.
Topper's Solved these Questions
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Exercises
57 Videos
- THE FORCESBOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Questions for short Answer
9 Videos
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer
16 Videos
Similar Questions
S1: The particles speed can never be equal to the wave speed in sine wave if the amplitude is less then wavelength divided by 2π.
S2: In transverse wave of amplitude A, the maximum particle velocity is four times its wave velocity. Then, the wave length of the wave is πA
S3: the phase difference between two points separated by 1m in a wave of frequency 120 Hz is 90∘. the velocity of the wave is 480 m/s
View SolutionAssertion : On a curved path, average speed of a particle can never be equal to average velocity.
Reason : Average speed is total distance travelled divided by total time. Whereas average velocity is, final velocity plus initial velocity divided by two.
View SolutionFigure shows a plot of the transverse displacements of the particles of a string at t = 0 through which a travelling wave is passing in the positive x-direction. The wave speed is 20cms−1. Find (a) the amplitude, (b) the wavelength, (c) the wave number and (d) the frequency of the wave.
 .
.
View SolutionFigure shows a plot of the transverse displacement of the particle of a string at t=0 through which a travelling wave is passing in the positive in the positive x-direction. The wave speed is 20cm/s. Find (a) the amplitude (b) the wavelength (c) the wave number and (d) the frequency of the wave.

View SolutionHow does the speed of sound change with change in wavelength of sound wave ?
View SolutionThe equation of a travelling sound wave is y=6.0sin(600t−1.8x) where y is measured in 10−5m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed.
View SolutionThe speed of electmagnetic waves in vacuum is equal to
View SolutionFigure below shows the distance-displacement graph of two waves A and B. Compare (i) the amplitude, (ii) the wavelength of the two waves.
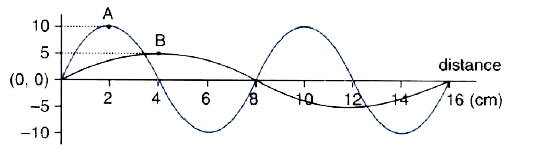
View SolutionWrite the relation for the speed of electromagnetic wave in terms of the amplitudes of electric and magnetic fields.
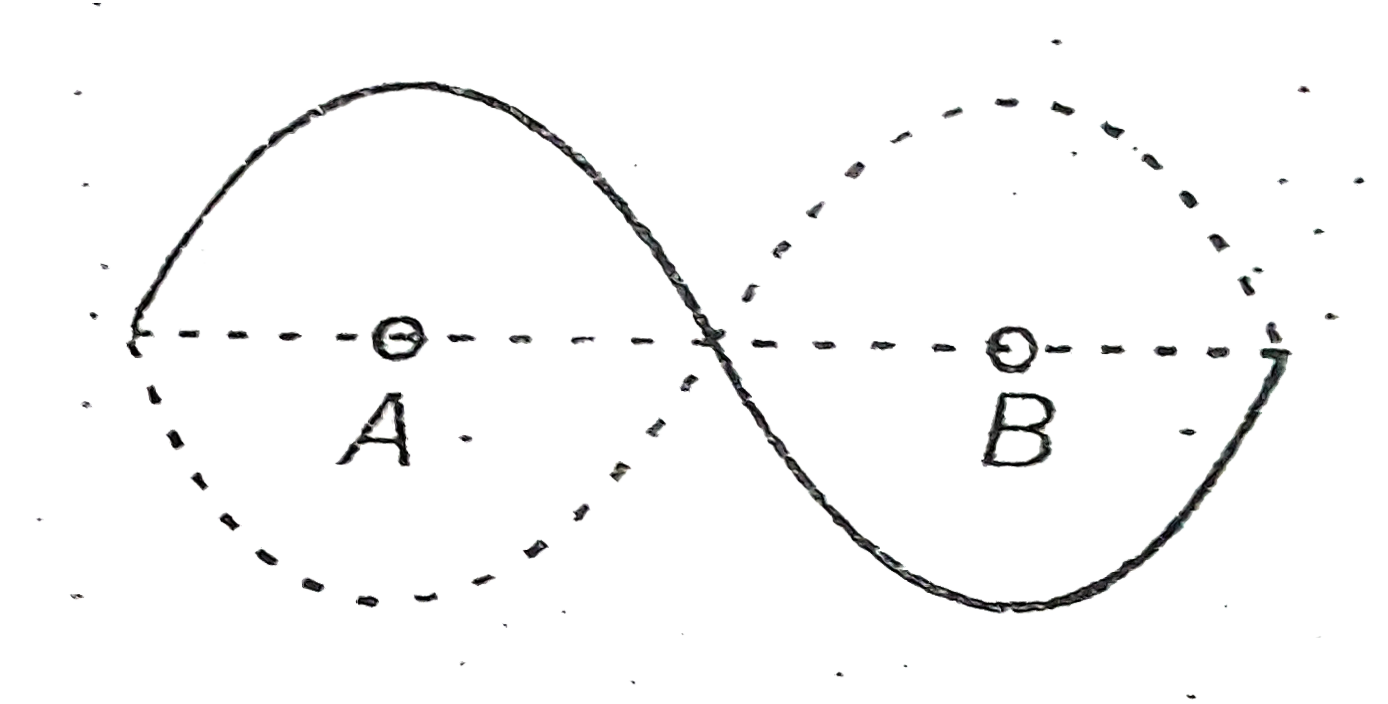
View SolutionIn a standing wave particles at the positions A and B, have a phase difference of
View Solution
