The inverse square law of intensity (i.e., the intensity is valid for a
1.point source
2.line source
3.plane source
4.cylindrical source.
The correct Answer is:A
To solve the question regarding the inverse square law of intensity, we need to analyze the different types of sources and how they emit light or energy. The question asks which type of source the inverse square law applies to: point source, line source, plane source, or cylindrical source.
1. Understanding Intensity:
- Intensity (I) is defined as the power (P) per unit area (A). Mathematically, it can be expressed as:
I=PA
2. Surface Area Consideration:
- For a point source, the energy radiates uniformly in all directions, forming a sphere around the source. The surface area (A) of a sphere is given by:
A=4πr2
- Therefore, the intensity at a distance r from the point source can be expressed as:
I=P4πr2
- This shows that intensity is inversely proportional to the square of the distance from the source, confirming the inverse square law.
3. Analyzing Other Sources:
- Line Source: A line source emits energy along a line. The intensity does not decrease with the square of the distance but rather depends on the geometry of the line, leading to a different relationship.
- Plane Source: A plane source emits energy uniformly over a plane. The intensity decreases with distance, but not according to the inverse square law.
- Cylindrical Source: Similar to the line source, a cylindrical source radiates energy in a cylindrical manner, which does not follow the inverse square law.
4. Conclusion:
- The inverse square law of intensity is valid only for a point source. This is because the energy spreads out uniformly in three-dimensional space, leading to the intensity being inversely proportional to the square of the distance from the source.
Final Answer:
The inverse square law of intensity is valid for a point source.
---
- Intensity (I) is defined as the power (P) per unit area (A). Mathematically, it can be expressed as:
I=PA
- For a point source, the energy radiates uniformly in all directions, forming a sphere around the source. The surface area (A) of a sphere is given by:
A=4πr2
- Therefore, the intensity at a distance r from the point source can be expressed as:
I=P4πr2
- This shows that intensity is inversely proportional to the square of the distance from the source, confirming the inverse square law.
- Line Source: A line source emits energy along a line. The intensity does not decrease with the square of the distance but rather depends on the geometry of the line, leading to a different relationship.
- Plane Source: A plane source emits energy uniformly over a plane. The intensity decreases with distance, but not according to the inverse square law.
- Cylindrical Source: Similar to the line source, a cylindrical source radiates energy in a cylindrical manner, which does not follow the inverse square law.
- The inverse square law of intensity is valid only for a point source. This is because the energy spreads out uniformly in three-dimensional space, leading to the intensity being inversely proportional to the square of the distance from the source.
The inverse square law of intensity is valid for a point source.
Topper's Solved these Questions
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Objective -2
10 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Exercises
41 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - worked out Examples
11 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
Similar Questions
Find the maxinum intensity in case of interference of n identical waves each of intensity I0 if the interference is
(a) coherent and (b) incoherent.
View SolutionThe black body spectrum of an object O1 is such that its radiant intensity (i.e. intensity per unit wavelength interval) is maximum at a wavelength of 200 nm. Another object O2 has the maximum radiant intensity at 600 nm. The ratio of power emitted per unit area by source O1 to that of source O2 is
View Solution
Knowledge Check
Inverse square law of distance is followed by
AGravitational forcesBElectromagnetic forcesCBoth (a) and (b)DNeither (a) and nor (b)Assertion: Magnetic force between two short magnets, when they are co-axial follows inverse square law of distance.
Reason: The magnetic forces between two poles do not follow inverse square law of distance.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true and reason is not the correct explanation of assertion.CIf assertion is ture but reason is false.DIf both assertion and reason are false.
A : For best contrast between maxima and minima in the interference pattern of Young.s double slit experiment, the intensity of light emerging out of the two slits should be equa.
R : The intensity of interference pattern is proportional to square of amplitude.
View SolutionAssertion (A): The nucleus of gold is stable even though there is a very strong coulombic repulsion among the protons.
Reason (R): The inverse square coulomb force is exactly balanced by another inverse square force which is very powerful. i.e., nuclear force.
View SolutionIn the photoelectric effect experiment, if f is the frequency of radiation incident on the metal surface and I is the intensity of the intensity radiations, then match the following columns:
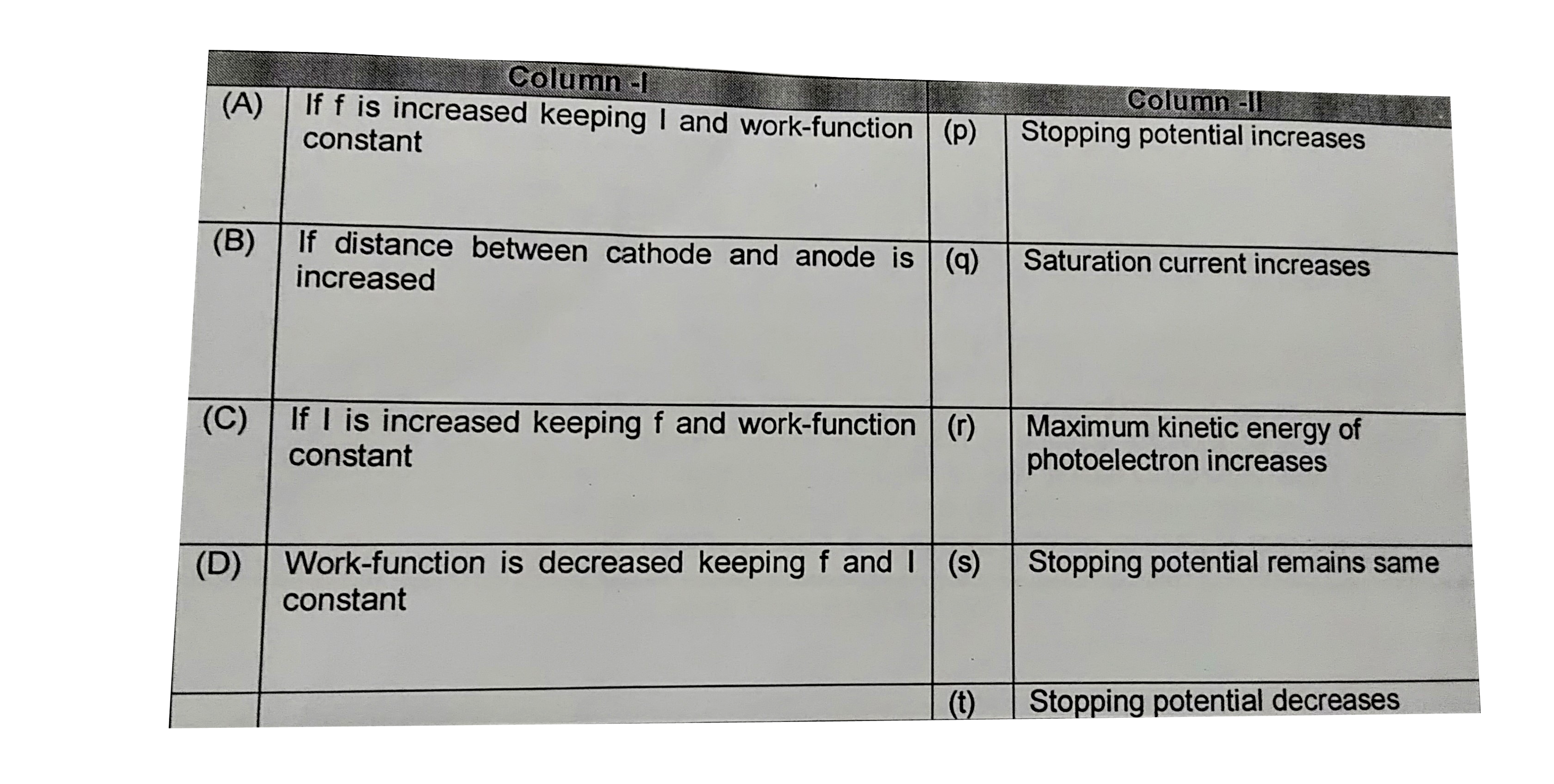
View SolutionIn Newton's inverse square law of gravitation had some dependence of radial distance other than r−2 which on of kepler's three laws of planetary motion would unchanged ?
View SolutionA charge Q is placed at the centre of a square If electric field intensity due to the charge at the corners of the square is E1 and the intensity at the mid point of the sidde of square is E2 then the ratio of E1E2 will be
View Solution(a) Explain the terms energy density and intensity of wave.
(b) Show that the intensity of a wave is proportional to the square of the amplitude.
View Solution
