A professor reads a greeting card received on his 50th birthday with + 2.5 D glasses keeping the card 25 cm away. Ten years later, he reads his farewell letter with the same glasses but he has to keep the letter 50 cm away. What power of lens should he now use?
The correct Answer is:D
To solve the problem, we need to determine the power of the lens that the professor should use to read his farewell letter, given that he has to keep the letter 50 cm away.
1. Understanding the Initial Conditions:
- The professor used glasses with a power of +2.5 D to read a greeting card at a distance of 25 cm.
- The power of the lens (P) is given by the formula:
P=1f(in meters)
- Therefore, the focal length (f) can be calculated as:
f=1P=12.5=0.4 m=40 cm
2. Setting Up the Lens Formula:
- The lens formula is given by:
1f=1v−1u
- Here, u is the object distance (negative for real objects), and v is the image distance.
3. Calculating Image Distance for the Greeting Card:
- For the greeting card, the object distance u=−25 cm.
- We need to find v:
140=1v−1−25
- Rearranging gives:
1v=140+125
- Finding a common denominator (200):
1v=5200+8200=13200
- Therefore:
v=20013≈15.38 cm
4. Calculating Image Distance for the Farewell Letter:
- Now, the professor reads the farewell letter at a distance of 50 cm, so u=−50 cm.
- Using the lens formula again:
1f=1v−1u
- We need to find v when u=−50 cm:
1f=1v−1−50
- Rearranging gives:
1v=1f+150
5. Finding the New Focal Length:
- We know that the professor can still see the image clearly, so we assume he wants the image to be formed at a distance of 200 cm (the distance he can comfortably see).
- Thus, substituting v=200 cm into the lens formula:
1f=1200+150
- Finding a common denominator (200):
1f=1200+4200=5200
- Therefore:
f=2005=40 cm
6. Calculating the New Power of the Lens:
- The power of the lens is given by:
P=1f(in meters)
- Converting focal length to meters:
f=0.4 m
- Therefore:
P=10.4=2.5 D
7. Final Calculation for New Power:
- Since he now needs to read at a distance of 50 cm, we need to find a new power:
P=1f=92=4.5 D
Conclusion:
The professor should now use glasses with a power of +4.5 D to read his farewell letter comfortably at 50 cm.
- The professor used glasses with a power of +2.5 D to read a greeting card at a distance of 25 cm.
- The power of the lens (P) is given by the formula:
P=1f(in meters)
- Therefore, the focal length (f) can be calculated as:
f=1P=12.5=0.4 m=40 cm
- The lens formula is given by:
1f=1v−1u
- Here, u is the object distance (negative for real objects), and v is the image distance.
- For the greeting card, the object distance u=−25 cm.
- We need to find v:
140=1v−1−25
- Rearranging gives:
1v=140+125
- Finding a common denominator (200):
1v=5200+8200=13200
- Therefore:
v=20013≈15.38 cm
- Now, the professor reads the farewell letter at a distance of 50 cm, so u=−50 cm.
- Using the lens formula again:
1f=1v−1u
- We need to find v when u=−50 cm:
1f=1v−1−50
- Rearranging gives:
1v=1f+150
- We know that the professor can still see the image clearly, so we assume he wants the image to be formed at a distance of 200 cm (the distance he can comfortably see).
- Thus, substituting v=200 cm into the lens formula:
1f=1200+150
- Finding a common denominator (200):
1f=1200+4200=5200
- Therefore:
f=2005=40 cm
- The power of the lens is given by:
P=1f(in meters)
- Converting focal length to meters:
f=0.4 m
- Therefore:
P=10.4=2.5 D
- Since he now needs to read at a distance of 50 cm, we need to find a new power:
P=1f=92=4.5 D
The professor should now use glasses with a power of +4.5 D to read his farewell letter comfortably at 50 cm.
Topper's Solved these Questions
- OPTICAL INSTRUMENTSBOOK - HC VERMA ENGLISHCHAPTER - OPTICAL INSTRUMENTSEXERCISE - Question for short Answer
12 Videos
- OPTICAL INSTRUMENTSBOOK - HC VERMA ENGLISHCHAPTER - OPTICAL INSTRUMENTSEXERCISE - Objective-2
5 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
- PERMANENT MAGNETSBOOK - HC VERMA ENGLISHCHAPTER - PERMANENT MAGNETSEXERCISE - Short Answer
11 Videos
Similar Questions
The ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
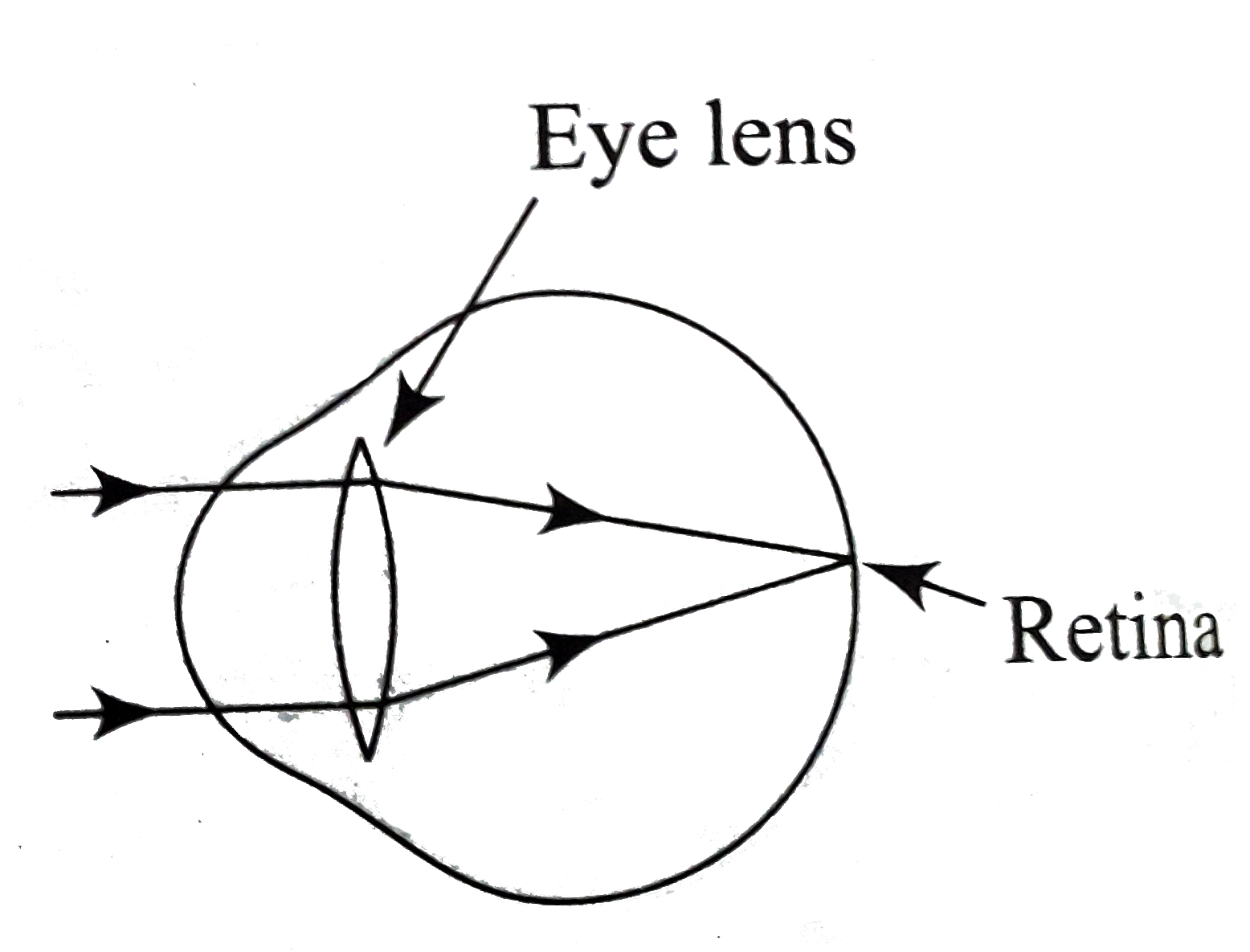
Q. A far sighted man connot see objects clearly unless they are at least 100cm from his eyes. The number of the spectacle lenses that will make his range of clear vision equal to an average grown up person will be
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
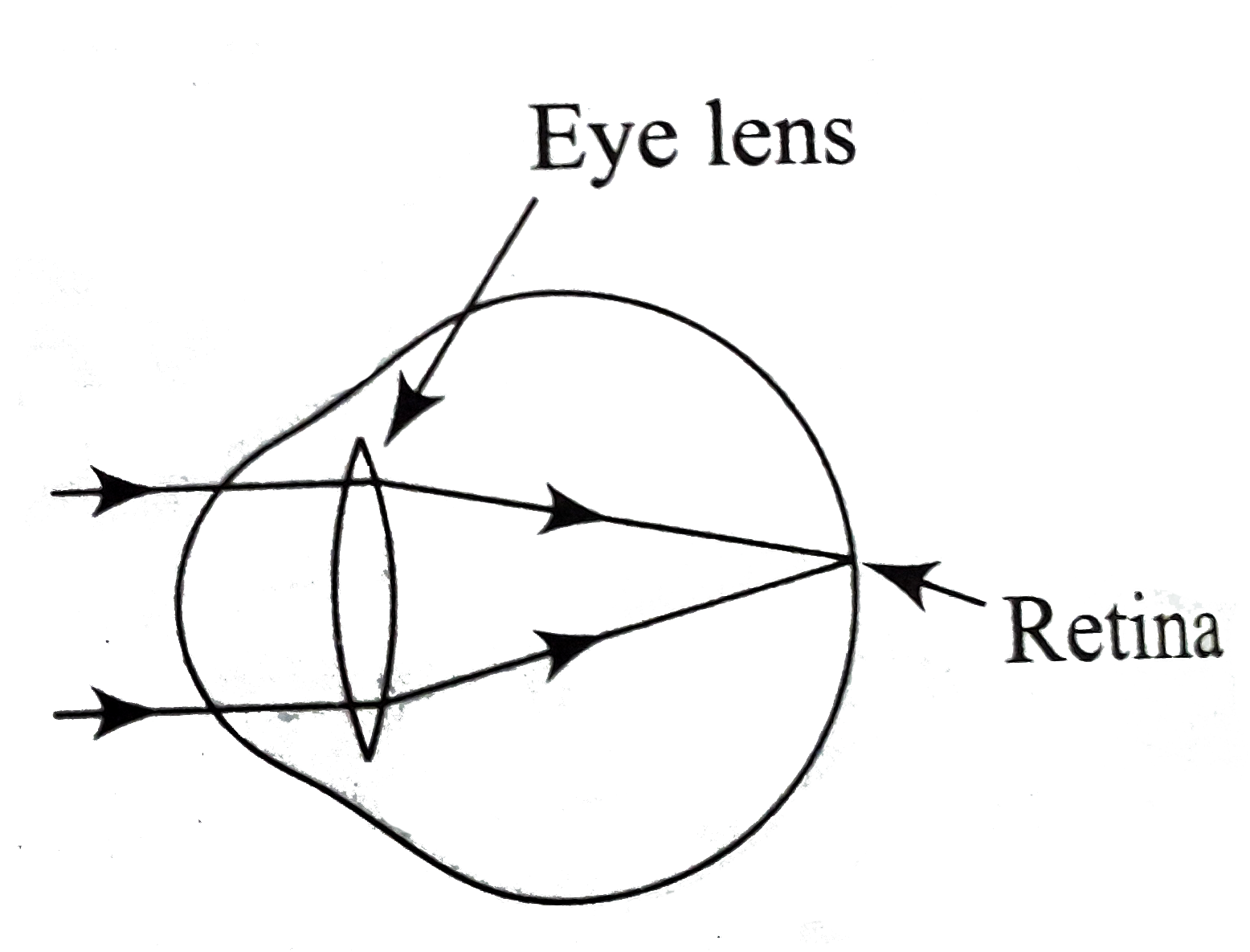
Q. A near sighted man can clearly see ojects only upto a distance of 100cm and not beyond this. The number of the spectacle lenses necessary for the remedy of this defect will be
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
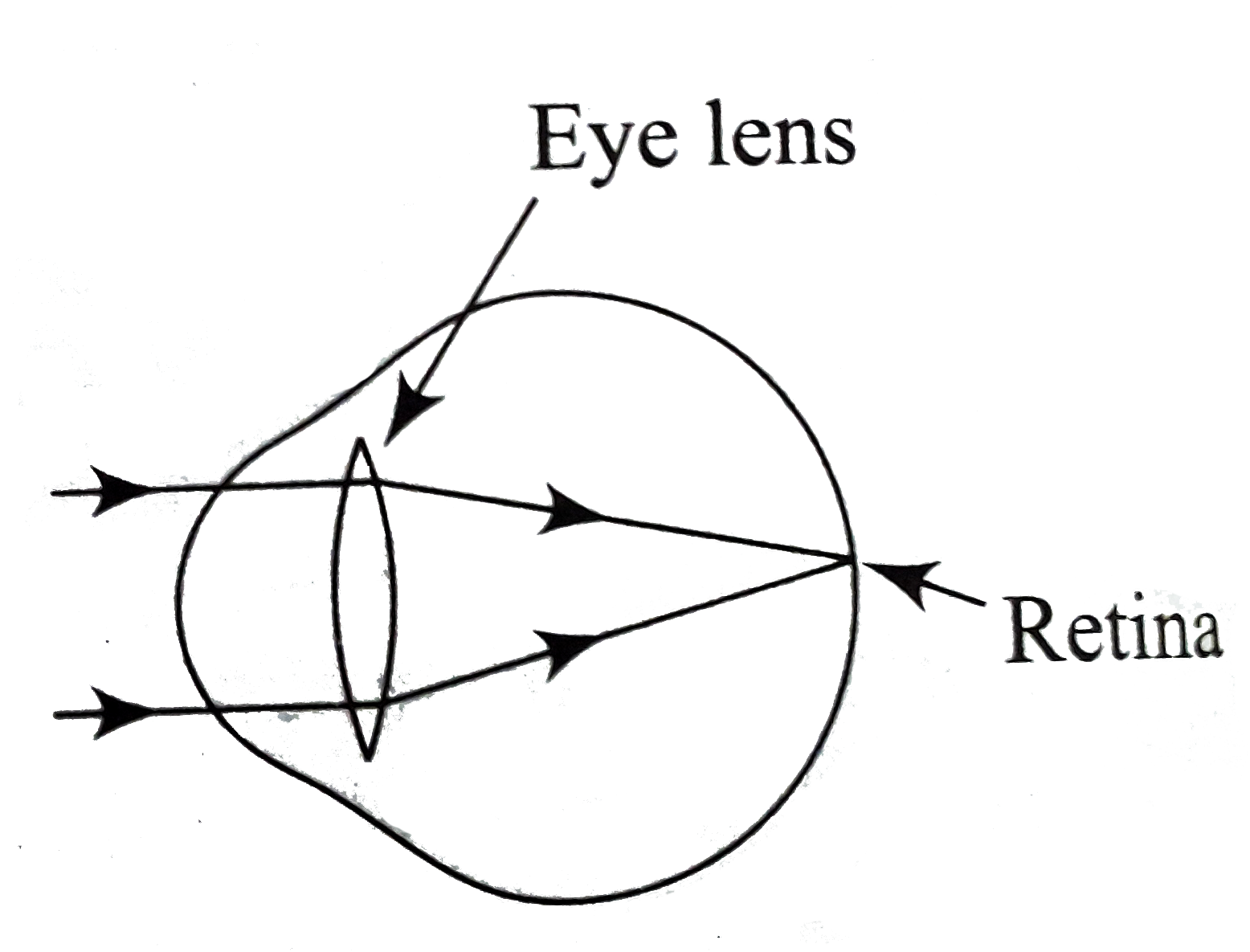
Q. A person can see objects clearly from distance 10cm to ∞. Then, we can say that the person is
View SolutionThe near point and far point of a person are 40cm and 250cm, respectively. Determine the power of lens he/she should use while reading a bool kept at distance 25cm away from it,
View SolutionQuestion 37 and 38 refer to the following information
The U.S. federal Government tracks the Consumer Price Index (CPI)- a comprehensive standard used to estimate the average price change for the typical goods and services purchased by consumers. This measure gives economics a useful way to estimate the rates of the inflation or deflation, which reflects the respective general increase or decrease of prices of goods and services in the economy. The accompanying tables summarizes the changes in the CPI for the years 2005 through 2014, which can be assumed to be the corresponding percent rates of inflation.
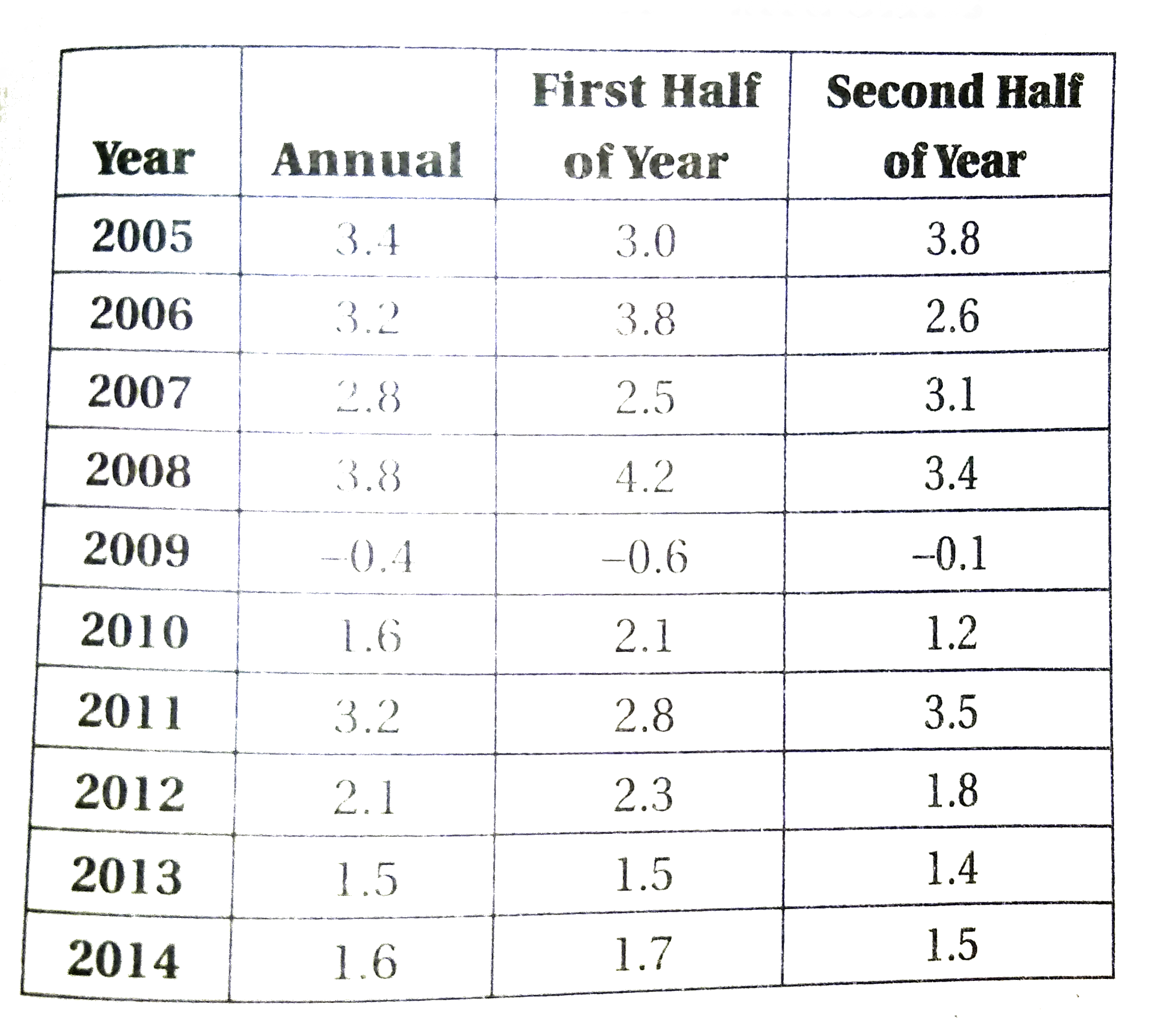
Q. At a beginning of 2015, a retired person is shopping for a retirement annunity, which is an investment policy that will give him fixed monthly payments for the rest of his life. He would like the amount of his annuity payments to more than keep up with the rate of inflation. He decides that he will choose a policy that issuse payments that increase annually at a rate of that is at least 1.5% greater than the average yearly compounded rate of inflation calculated from the period that extends from the second half of 2005 through the first half of 2008. What should be the minimum annual rate of increase in his monthly annuity payments, correct to the nearest tenth?
View SolutionA far sighted person has a near point of 60cm . What power lens should be used for eye glasses such that the person can be read this book at a distance of 25 cm.
View SolutionA student focussed the flame of a candle on a screen with the help of a convex lens. He noted the positions of candle, lens and screen on the scale as given below:
Position of candle = 14.0 cm, Position of convex lens = 50.0 cm, Position of screen = 86.0 cm
(i) Find the focal length of the lens.
(ii) If under the given condition, height of the flame is 1.5 cm, what would be the height of image obtained on the screen?
(iii) If he displaces the candle to 32.0 cm, where will the image be formed and what will be its nature? Give reason for your answer.
(iv) After this if he further displaces the candle towards the lens, what will be the nature of the image formed and where will it be?
(v) Draw a ray diagram to show the formation of image in the above mentioned case.
[Hints. (i) u = (50-14) cm = 36 cm, v = (86 - 50) cm = 36 cm.
Thus the object is at 2f. Therefore f = 18cm
(ii) Height will be same, i.e., 1.5 cm
(iii) u = 50-32 = 18 cm. Thus, object will be at focus. Therefore, image will be at infinity and is real, inverted and enlarged.
(iv) Object will come in between focus and optical centre.
Image will be virtual, erect and enlarged and formed on the same side of lens as the object.
View SolutionA perosn decides to use his bath tub water to generate electric power to run a 40W bulb. The bath tub is located at a height of 10m from the ground and it holds 200 litres of water. He instals a water driven wheel generator on the ground. At what rate should the water drain from the bath tub to light the bulb? How long can he keep the bulb on , if bath tub was full initially ? Efficiency of generator is 90%. Take g=9.8m/s2
View SolutionAn inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed v0. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
Just as the student starts his free fall, he presses the button of the stopwatch. When he reaches at the top of 100th floor, he has observed the reading of stopwatch as 00:00:06:00. What should be the initial downward speed of the rocketeer so that he catches the student at the top of 100 the floor for safe landing ?
View SolutionAn inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed v0. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
Just as the student starts his free fall, he presses the button of the stopwatch. When he reaches at the top of 100th floor, he has observed the reading of stopwatch as 00:00:06:00 (hh:mm:ss:100 th part of the second). Find the value of g. (correct upt ot two decimal places).
View Solution
