A perosn decides to use his bath tub water to generate electric power to run a 40W bulb. The bath tub is located at a height of 10m from the ground and it holds 200 litres of water. He instals a water driven wheel generator on the ground. At what rate should the water drain from the bath tub to light the bulb? How long can he keep the bulb on , if bath tub was full initially ? Efficiency of generator is 90%. Take g=9.8m/s2
The correct Answer is:4/9 kg/sec; 450 sec
To solve the problem step by step, we need to calculate the rate at which water should drain from the bathtub to generate enough power for a 40W bulb, and then determine how long the bulb can be kept on with the initial amount of water.
Step 1: Calculate the output power required from the generator
The power required to run the bulb is given as 40W. Since power is measured in joules per second, the generator must output 40 joules of energy every second.
Hint: Remember that power is defined as energy per unit time.
Step 2: Account for the efficiency of the generator
The efficiency of the generator is given as 90%. This means that only 90% of the input energy is converted to output energy. Therefore, the input energy required can be calculated using the formula:
Input Power=Output PowerEfficiency=40W0.9≈44.44W
Hint: Efficiency is the ratio of useful output energy to input energy, expressed as a percentage.
Step 3: Calculate the energy required per second
Since the input power is approximately 44.44W, this means that the generator needs to convert this amount of energy from the falling water every second.
Hint: Remember that 1 Watt = 1 Joule/second.
Step 4: Calculate the gravitational potential energy per unit mass
The gravitational potential energy (PE) for a mass m falling from a height h is given by:
PE=m⋅g⋅h
Where:
- g=9.8m/s2 (acceleration due to gravity)
- h=10m (height of the bathtub)
Thus, the energy per unit mass (for 1 kg of water) falling from 10m is:
PE=1⋅9.8⋅10=98J/kg
Hint: Gravitational potential energy depends on the height from which the mass falls and the acceleration due to gravity.
Step 5: Calculate the mass flow rate required
To find the mass flow rate (˙m) required to generate the necessary power, we can use the relationship:
Power=mass flow rate⋅energy per unit mass
Rearranging gives:
˙m=PowerEnergy per unit mass=44.44W98J/kg≈0.453kg/s
Hint: The mass flow rate tells us how much mass needs to fall per second to generate the required power.
Step 6: Calculate the total mass of water in the bathtub
The bathtub holds 200 liters of water. Since the density of water is 1 kg/L, the total mass of water is:
mi=200kg
Hint: The density of water is a key factor in converting volume to mass.
Step 7: Calculate the time the bulb can be kept on
Now we can find out how long the bulb can be kept on by dividing the total mass of water by the mass flow rate:
t=mi˙m=200kg0.453kg/s≈441s
Hint: The time the bulb can be kept on is determined by the total mass of water and the rate at which it is used.
Final Answers
1. The rate at which the water should drain from the bathtub is approximately 0.453 kg/s.
2. The bulb can be kept on for approximately 441 seconds.
The power required to run the bulb is given as 40W. Since power is measured in joules per second, the generator must output 40 joules of energy every second.
The efficiency of the generator is given as 90%. This means that only 90% of the input energy is converted to output energy. Therefore, the input energy required can be calculated using the formula:
Since the input power is approximately 44.44W, this means that the generator needs to convert this amount of energy from the falling water every second.
The gravitational potential energy (PE) for a mass m falling from a height h is given by:
- g=9.8m/s2 (acceleration due to gravity)
- h=10m (height of the bathtub)
To find the mass flow rate (˙m) required to generate the necessary power, we can use the relationship:
The bathtub holds 200 liters of water. Since the density of water is 1 kg/L, the total mass of water is:
Now we can find out how long the bulb can be kept on by dividing the total mass of water by the mass flow rate:
1. The rate at which the water should drain from the bathtub is approximately 0.453 kg/s.
2. The bulb can be kept on for approximately 441 seconds.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exrcies-3(PART-2)
23 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.71
1 Videos
Similar Questions
Water is used to generate electricity.
View SolutionA water tank is 3m long, 2m broad and 1m deep. How many litres of water can it hold?
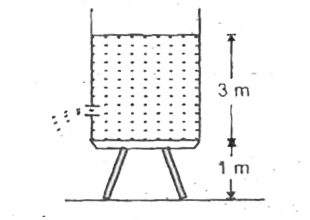
View SolutionWater is filled in a tank upto 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
View SolutionAn electric bulb of 314 watt is at a distance of 10cm from a point. If the efficiency of bulb is 50% then intensity at that point is
View SolutionIn a hydroelectric power plant more electrical power can be generated if water falls a greater height because :
View SolutionHot water of Manikaran is used for generating electricity. It is
View SolutionThe cytosol is the fluid that bathes the structures that are located in the cytoplasm.
View SolutionThe power of pump, which can pump 200 kg of water to a height of 50 m in 10 sec, will be
View SolutionA large tub is filled with 920 liters of water and 1,800 liters of alcohol. If 40% of the alcohol evaporates, what percemt of the remaining liquid is water?
View SolutionAn electric bulb is connected to a 220V generator. The current is 0.50A. What is the power of the bulb ?
View Solution
