Can the dispersive power ω=μv−μrμ−1 be negative? What is the sign of ω if a hollow prism is immersed into water?
To solve the question regarding the dispersive power ω=μv−μrμ−1, we will analyze the components of the equation step by step.
1. Understanding the Variables:
- μv: Refractive index of violet light.
- μr: Refractive index of red light.
- μ: Refractive index of the medium (in this case, we will consider both air and water).
2. Analyzing the Numerator:
- The numerator of the equation is μv−μr.
- It is known that the refractive index of violet light (μv) is always greater than that of red light (μr) in any medium. Therefore, μv−μr>0.
3. Analyzing the Denominator:
- The denominator is μ−1.
- For any medium other than air, the refractive index μ is greater than 1 (e.g., for water, μ≈1.33).
- Thus, μ−1>0 for all materials except air.
4. Combining the Results:
- Since both the numerator (μv−μr) and the denominator (μ−1) are positive, we can conclude:
ω=μv−μrμ−1>0
- Therefore, the dispersive power ω cannot be negative.
5. Considering the Case of a Hollow Prism Immersed in Water:
- When a hollow prism is immersed in water, the refractive indices remain the same in terms of their order: μv>μr.
- The refractive index of water is approximately 1.33, which is greater than 1.
- Thus, μ−1 remains positive, and since μv−μr is still positive, we have:
ω>0
- Therefore, even in water, the dispersive power ω remains positive.
Conclusion:
The dispersive power ω cannot be negative. When a hollow prism is immersed in water, ω remains positive.
- μv: Refractive index of violet light.
- μr: Refractive index of red light.
- μ: Refractive index of the medium (in this case, we will consider both air and water).
- The numerator of the equation is μv−μr.
- It is known that the refractive index of violet light (μv) is always greater than that of red light (μr) in any medium. Therefore, μv−μr>0.
- The denominator is μ−1.
- For any medium other than air, the refractive index μ is greater than 1 (e.g., for water, μ≈1.33).
- Thus, μ−1>0 for all materials except air.
- Since both the numerator (μv−μr) and the denominator (μ−1) are positive, we can conclude:
ω=μv−μrμ−1>0
- Therefore, the dispersive power ω cannot be negative.
- When a hollow prism is immersed in water, the refractive indices remain the same in terms of their order: μv>μr.
- The refractive index of water is approximately 1.33, which is greater than 1.
- Thus, μ−1 remains positive, and since μv−μr is still positive, we have:
ω>0
- Therefore, even in water, the dispersive power ω remains positive.
The dispersive power ω cannot be negative. When a hollow prism is immersed in water, ω remains positive.
Topper's Solved these Questions
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Exercises
11 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer
7 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer
17 Videos
Similar Questions
The equation ω=μv−μrμ−1 was derived for a prism having small refracting angle. Is it also valid for a prism of large refracting angle? Is it also valid for a glass slab or a glass sphere?
View SolutionA convex glass lens (μg=1.5) has a focal length of 8 cm when placed in air. What is the focal length of the lens when it is immersed in water ?
(μω=43)
View SolutionThe dispersive power (w) of the material of a prism is (where symbols have their usual meanings)
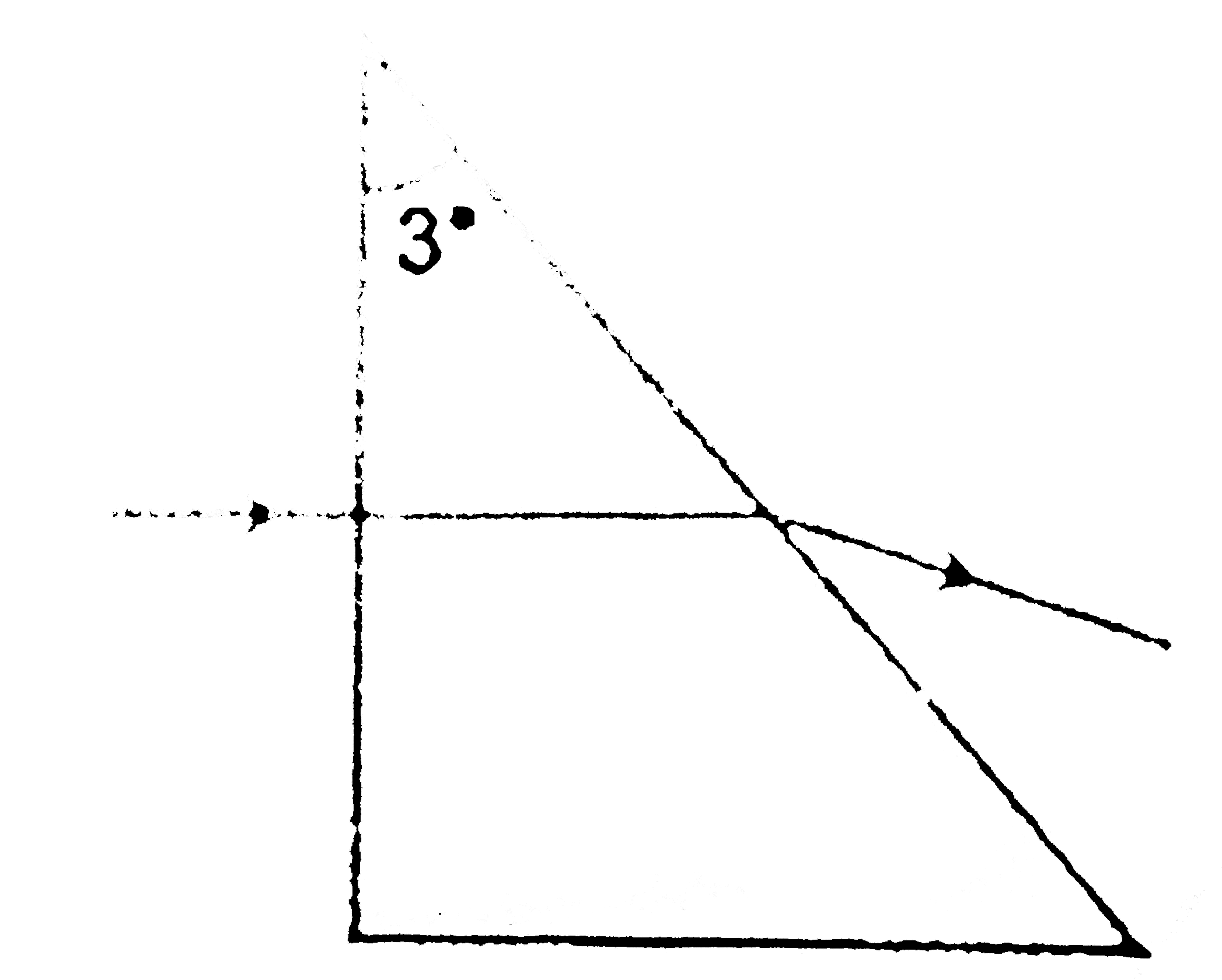
View SolutionFind the angle of devaition suffered by the light ray shown in figure for following two conditions. The refractive index for the prism material is μ=3/2.
(i) When the prism is placed in air 9μ=1)
(ii) When the prism is placed in water (μ=4/3)
View SolutionCalculate the dispersive power for crown glass from the given data
μv=1.523 and μr=1.5145.
View SolutionCalculate the dispersive power for crown glass from the given data
μv=1.523 and μr=1.5145.
View SolutionWhat is the relation between the refractive index of water with respect to air (aμw) and the refractive index of air with respect to water (wμa).
View SolutionIf the refractive index of water with respect to air (aμw) is 53. Calculate the refractive index of air with respect to water (wμa).
View SolutionWhen a ray of sun light passes through the prism, each colour of light has its own speed in the glass. The seven colours come out of the prism with different angles of deviation. Red deviates least and blue deviates maximum. Thus a prism can disperse a white light into seven colours which is called colour spectrum.

For a thin prism, the angle of deviation is given as δ=(n−1)A. The angle of dispersion is given as ϕ=δv−δr. The dispersive power of a prism is ω=ϕδmean=ϕδy
Using the above ideas, give answer the following questions.
A prism has R.I. for violet and red nv=1.523,nr=1.5145. If the angle of prism is A=2∘ the dispersive power of the prism is :
View SolutionA lens has a power of ±5 diopeters in air. What will be its power if completely immersed in water? (.aμw=4/3andaμg=3/2)
View Solution
