The overall luminous efficient of a 100 W electric lamp is 25 lumen W−1. Assume that light is emitted by the lamp only in the forward half, and is uniformly distributed in al diredctionsin this half. Calculate the luminous flux falling on a plane object of area 1cm2 placed at a distance of 50 cm from the lamp and perpendicular to the line joining the lamp and the object.
To solve the problem step by step, we will follow the outlined process in the video transcript, ensuring clarity and completeness.
Step 1: Calculate the Total Luminous Flux from the Lamp
Given:
- Power of the lamp = 100 W
- Luminous efficiency = 25 lumen/W
The total luminous flux (Φ) emitted by the lamp can be calculated using the formula:
Φ=Power×Luminous Efficiency
Substituting the values:
Φ=100W×25lumen/W=2500lumen
Step 2: Determine the Solid Angle of the Lamp
Since the lamp emits light only in the forward half, the solid angle (Ω) for a hemisphere is:
Ω=2πsteradians
Step 3: Calculate the Luminous Intensity of the Lamp
Luminous intensity (I) can be calculated using the formula:
I=ΦΩ
Substituting the values:
I=2500lumen2π≈25006.2832≈398.94lumen/steradian
Step 4: Calculate the Solid Angle Traced by the Plane Object
Given:
- Area of the plane object (A) = 1 cm² = 1×10−4m2
- Distance from the lamp (R) = 50 cm = 0.5 m
The solid angle (ΔΩ) traced by the plane can be calculated using the formula:
ΔΩ=AR2
Substituting the values:
ΔΩ=1×10−4m2(0.5m)2=1×10−40.25=4×10−4steradians
Step 5: Calculate the Luminous Flux Falling on the Plane Object
The luminous flux (Φ_plane) falling on the plane can be calculated using the formula:
Φplane=I×ΔΩ
Substituting the values:
Φplane=398.94lumen/steradian×4×10−4steradians≈0.159576lumen
Final Answer
The luminous flux falling on the plane object is approximately:
Φplane≈0.16lumen
---
Given:
- Power of the lamp = 100 W
- Luminous efficiency = 25 lumen/W
Φ=Power×Luminous Efficiency
Substituting the values:
Φ=100W×25lumen/W=2500lumen
Since the lamp emits light only in the forward half, the solid angle (Ω) for a hemisphere is:
Ω=2πsteradians
Luminous intensity (I) can be calculated using the formula:
I=ΦΩ
Substituting the values:
I=2500lumen2π≈25006.2832≈398.94lumen/steradian
Given:
- Area of the plane object (A) = 1 cm² = 1×10−4m2
- Distance from the lamp (R) = 50 cm = 0.5 m
ΔΩ=AR2
Substituting the values:
ΔΩ=1×10−4m2(0.5m)2=1×10−40.25=4×10−4steradians
The luminous flux (Φ_plane) falling on the plane can be calculated using the formula:
Φplane=I×ΔΩ
Substituting the values:
Φplane=398.94lumen/steradian×4×10−4steradians≈0.159576lumen
The luminous flux falling on the plane object is approximately:
Φplane≈0.16lumen
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - question for short answer13videos
PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITY
- BOOK - HC VERMA ENGLISHCHAPTER - SEMICONDUCTOR AND SEMICONDUCTOR DEVICESEXERCISE - Question for short answer11videos
SEMICONDUCTOR AND SEMICONDUCTOR DEVICES
Similar Questions
A 100 W sodium lamp is radiating light of wavelength 5890A, uniformly in all directions,
a. At what rate, photons are emitted from the lamp?
b. At what distance from the lamp, the average flux is 1 photon(cm2−s)−1?
c. What are the photon flux and photon density at 2m from the lamp?View SolutionA circular area of radius 1.0 cm is placed at a distance of 2.0 m from a poit source.Teh source emits light uniformluy in al directions. The line joining the sorce to the dcentre of the area is normal to the area. It ils found that 2.0×1−3 lumen of luminous flux is incident on the area. Calculate the total luminous flux emitted by the soure and teh luminous intensity of the source along the axis of the area.
View SolutionTwo media each of refractive index 1.5 with plane parallel boundaries are separated by 100cm. A convex lens of focal length 60cm is placed midway between them with its principal axis normal to the boundaries. A luminous point object O is placed in one medium on the lens at a distance 125cm from it. Find the position of its image formed as a result of refraction through the system.
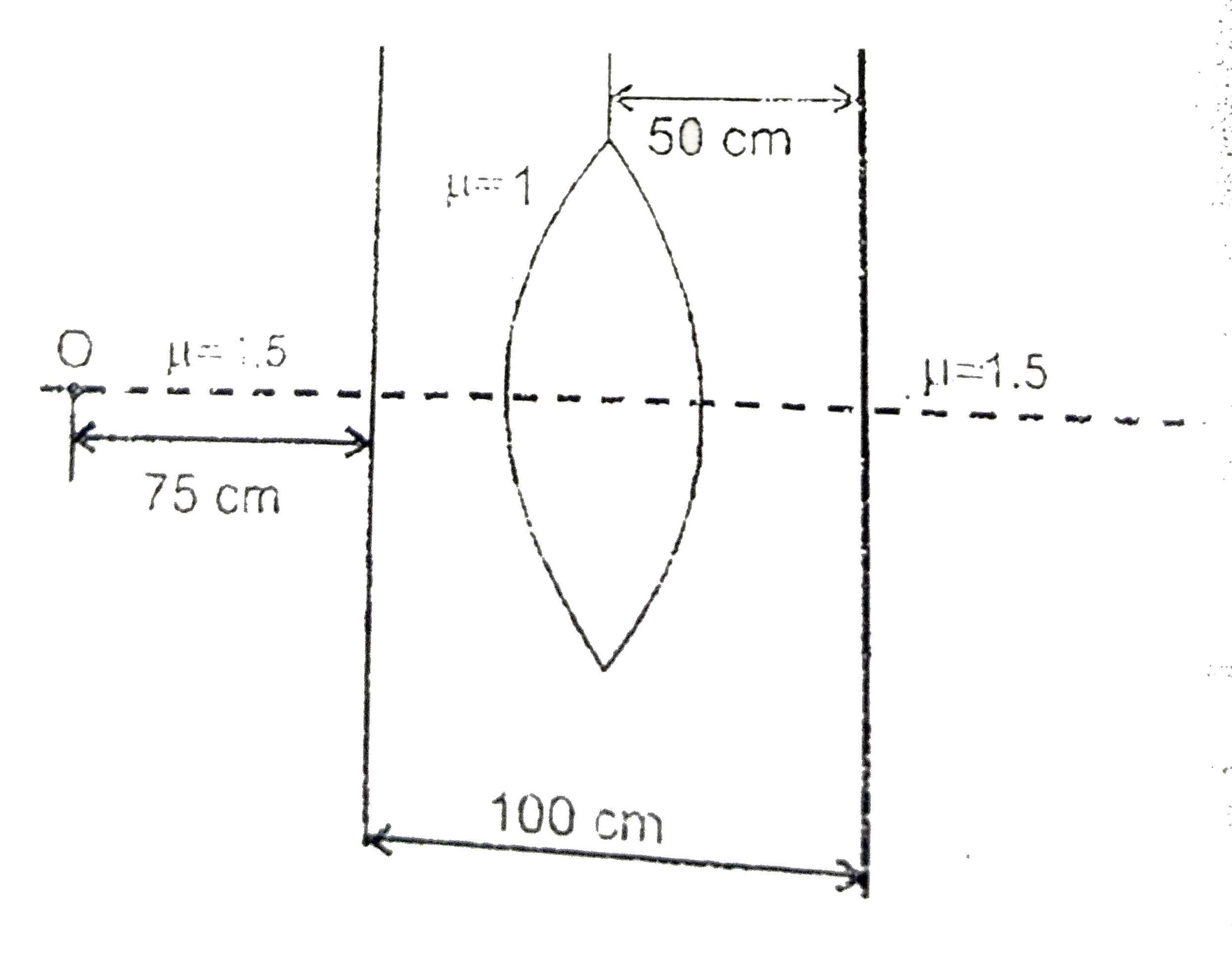 View Solution
View SolutionA point source is emitting 0.2 W of ultravio- let radiation at a wavelength of λ=2537Å. This source is placed at a distance of 1.0m from the cathode of a photoelectric cell. The cathode is made of potassium (Work function =2.22eV) and has a surface area of 4cm2.
(a) According to classical theory, what time of exposure to the radiation shall be required for a potassium atom to accumulate sufficient energy to eject a photoelectron. Assume that radius of each potassium atom is 2 Å and it absorbs all energy incident on it.
(b) Photon flux is defined as number of light photons reaching the cathode in unit time. Calculate the photon flux.
(c) Photo efficiency is defined as probability of a photon being successful in knocking out an electron from the metal surface. Calculate the saturation photocurrent in the cell assuming a photo efficiency of 0.1.
(d) Find the cut – off potential difference for the cell.View SolutionWhen a current through the medium, an electric field exists as well as a potential which varies in space. Suppose that there is a break in a high - voltage transmission line and the free end of a wire of length L is lying on the ground. An electric current flows through the regions of soil adjoining the conductor. If a man happens to be walking near by a potential difference, which is called the step voltage appears between the points where his feet touch the ground, Consequently, an electric current whose strength depends on this potential difference flows through the man.
Let us calculate the step voltage. Since the conductor is quite long, we assume that the current flows from it to the ground in a direction perpendicular to the conductor. The equipotential surfaces are the surfaces of semi-cylinders whose axes coincide with the conductor. Suppose that the man is walking in a direction perpendicular to the conductor with a step of length 'b' the distance between the conductor and the foot closer to it being d. Assuming that the current flows uniformly from the conductor over the semi cylindrical region we obtain the following expression for the current density at a distance from the conductor:
j=iπrL
In this case , the field strength along the radii perpendicular to the conductor is Er=jσ=lπrLσ
Consequently , the step voltage is Vst=∫d+bdEdr=1πσLln(d+bd)
For example , If l=500A , d=1 m , b=65 cm and L=30 m we find that Vst=270 V. Much higher voltages may appear under other conditions and other shapes of conductors.
When a part of a high- voltage transmission line falls on the ground, it creates a hazardView SolutionCalculate the number of photons emitted by a 100W yellow lamp in 1.0s. Take the wavelength of yellow light as 560nm and assume 100 percent efficiency.
View SolutionA meacury arec lamp provides 0.1 watt of ultra-violet radiation at a wavelength of λ=2537Å only. The photo tube (cathode of photo electric device) consists of potessium and has an effective area of 4cm2. The cathode is located at a distance of 1m from the radiation source. The work funcation for potassium is ϕ0=2.22eV.
According to classical theory, the radiation from arc lamp spreads out uniformaly in space as spherical wave. What time of expource to the radiation should be required for a potassium atom (radius 2Å) ub tge cathode to accumulate sufficient enerfy to eject a photo-electron?View SolutionAn equi-convex lens of focal length F in air is is cut into two halves along the plane perpendicular to the optic axis. One of the halves is placed between a fixed object and a screen separated by distance of 90 cm . Two images are formed on the screen for two different positions of the lens with magnification 2 and 1/2 respectively. Find the value of F . what would be the value of the focal length of the equiconvex lens if the lens is immersed in water ? Refractive index of the material of the lens is 1.5 and that of water is μw=4/3.
View SolutionA mercury arc lamp provides 0.10 W of UV radiation at a wavelength of λ=2537Å(all other wavelenghts having been absorbed by filters). The cathode of photoelectric device (a photo-tube) consists of potassium and has an effective area of 4cm2. The anode is located at a distance of 1 m from radiation source. The work function for potassium is ϕ0=2.22eV.
(a) According to classical theory, the radiation from the arc spreads out uniformly in space as spherical wave. What time of exposure to the radiation should be required for a potassium atoms(radius 2 Å) in the anode to accumulate sufficient energy to eject a photo-electron?
(b) What is the energy of a single photon from the source?
(C) What is the flux of photons(number per second) at the cathode? To what saturation current does this flux correspond if the photo-conversion efficiency is 5% (i.e. if each photon has a probability of 0.05 of ejecting an electron).
(d) what is the cutt off potential V0?View SolutionAn experimental setup of verification of photoelectric effect is shown in the diagram. The voltage across the electrode is measured with the help of an ideal voltmetar, and which can be varied by moving jockey 'J' on the potentiometer wire. The battery used in potentiometer circuit is of 20 V and its internal resistance is 2ω. The resistance of 100cm long potentiometer wire is 8ω. The photo current is measured with the help of an ideal ammeter. Two plates of potassium oxide of area 50cm2 at separation 0.5mm are used in the vacuum tube. Photo current in the circuit is very small so we can treat potentiometer circuit an indepdent circuit. The wavelength of various colours is as follows :
_E01_157_Q01.png)
∣∣ ∣∣Light1Violet2Blue3Green4Yellow5Orange6RedλinÅ→4000−45004500−50005000−55005500−60006000−65006500−7000∣∣ ∣∣
It is found that ammeter current remians unchanged (2μA) even when the jockey is moved from the 'P' to the middle point of the potentiometer wire. Assuming all the incident photons eject electron and the power of the light incident is 4×10−6W. Then colour of the incident light is :View Solution

