A sound wave of frequency 100 Hz is travelling in air. The speed of sound in air is 350ms−1 (a) By how much is the phase changed at a given point in 2.5 ms ? (b) What is the phase difference at a given instant between two points separated by a distance of 10.0 cm along the direction of propagation ?
The correct Answer is:A, B, C
To solve the problem step by step, we will break it down into two parts as per the question.
Part (a): Phase Change at a Given Point in 2.5 ms
Step 1: Calculate the distance travelled by the sound wave in 2.5 ms.
- Given:
- Speed of sound (v) = 350 m/s
- Time (t) = 2.5 ms = 2.5 × 10^-3 s
- Distance (d) = Speed × Time
d=v×t=350m/s×2.5×10−3s=0.875m
Step 2: Calculate the wavelength (λ) using the frequency (f).
- Given:
- Frequency (f) = 100 Hz
- The relationship between speed, frequency, and wavelength is:
v=f×λ⟹λ=vf=350m/s100Hz=3.5m
Step 3: Calculate the phase change (Δφ) using the formula.
- The formula for phase change is:
Δϕ=2πλ×d
- Substitute the values:
Δϕ=2π3.5×0.875
- Simplifying:
Δϕ=2π×0.8753.5=2π×0.8753.5=2π×0.8753.5=1.75π3.5=π2
Part (b): Phase Difference Between Two Points Separated by 10.0 cm
Step 1: Convert the distance from cm to m.
- Given:
- Distance (d) = 10.0 cm = 0.1 m
Step 2: Calculate the phase difference (Δφ) using the same formula.
- Using the same formula for phase difference:
Δϕ=2πλ×d
- Substitute the values:
Δϕ=2π3.5×0.1
- Simplifying:
Δϕ=2π×0.13.5=0.2π3.5=0.2π3.5=2π35
Final Answers:
(a) The phase change at a given point in 2.5 ms is π2.
(b) The phase difference at a given instant between two points separated by a distance of 10.0 cm is 2π35.
- Given:
- Speed of sound (v) = 350 m/s
- Time (t) = 2.5 ms = 2.5 × 10^-3 s
- Distance (d) = Speed × Time
d=v×t=350m/s×2.5×10−3s=0.875m
- Given:
- Frequency (f) = 100 Hz
- The relationship between speed, frequency, and wavelength is:
v=f×λ⟹λ=vf=350m/s100Hz=3.5m
- The formula for phase change is:
Δϕ=2πλ×d
- Substitute the values:
Δϕ=2π3.5×0.875
- Simplifying:
Δϕ=2π×0.8753.5=2π×0.8753.5=2π×0.8753.5=1.75π3.5=π2
- Given:
- Distance (d) = 10.0 cm = 0.1 m
- Using the same formula for phase difference:
Δϕ=2πλ×d
- Substitute the values:
Δϕ=2π3.5×0.1
- Simplifying:
Δϕ=2π×0.13.5=0.2π3.5=0.2π3.5=2π35
(a) The phase change at a given point in 2.5 ms is π2.
Topper's Solved these Questions
Similar Questions
A sound wave of frequency 80Hz is travelling with speed 320m/s.
(a) Find the change in phase at a given position in 400ms
(b) Find the phase difference between two positions seperated by 20cm at a particular instant.View SolutionThe speed of a wave in a streched string is 20ms−1 and its frequency is 50 Hz. Calculate the phase difference in radian between two points situated at a distance of 10 cm on the string.
View SolutionA sound wave of frequency 10 kHz is travelling in air with a speed of 340ms−1. Find the minimum separation between two points where the phase difference is 60∘.
View SolutionThe phase difference between two points separated by 0.8 m in a wave of frequency 120 Hz is 0.5π . The wave velocity is
View SolutionA progressive wave moves with a velocity of 36m/ s in a medium with a frequency of 200Hz. The phase difference between two particles seperated by a distance of 1 cm is
View SolutionWhat is the minimum distance between two points in a wave having a phase difference 2π ?
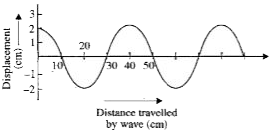
View SolutionA wave travelling along the length of a string is shown in Fig. 14.4.12. Using the scale on the given axis, find
(i) The amplitude of the wave
(ii) The wavelength of the wave
(iii) If the frequency of the wave is 10 Hz, What is the speed of the wave?
(iv) What is the initial phase of the wave ?
(v) What is the phase difference between two points separated by a distance 10 cm ?
(vi) If this wave is made to travel through water what is the wavelength of the wave, if the speed of, the waves in water is 10 m/s.
 View Solution
View SolutionA wave of frequency 20 Hz is propagatinig is space with speed 200 m/s. the phase difference of the two points of wave separated by a distance 5 m is
View SolutionA progressive wave of frequency 550 Hz is travelling with a velocity of 360 ms How far apart are the two points 60∘ out of phase ?
View SolutionA sound wave travelling in water has wavelength 0.4 m.
Is this wave audible in air ? (The speed of sound in water = 1400ms−1)View Solution

