The speed of a wave in a streched string is 20ms−1 and its frequency is 50 Hz. Calculate the phase difference in radian between two points situated at a distance of 10 cm on the string.
π2
π
3π2
2π
The correct Answer is:A
To solve the problem of finding the phase difference between two points on a stretched string, we can follow these steps:
Step 1: Identify the given values
- Speed of the wave (v) = 20 m/s
- Frequency (f) = 50 Hz
- Distance between the two points (Δx) = 10 cm = 0.1 m
Step 2: Calculate the wavelength (λ)
The wavelength can be calculated using the formula:
λ=vf
Substituting the known values:
λ=20m/s50Hz=2050=0.4m
Step 3: Use the formula for phase difference (Δφ)
The phase difference (Δφ) between two points separated by a distance Δx is given by the formula:
Δϕ=2πΔxλ
Substituting the values we have:
Δϕ=2π×0.1m0.4m
Step 4: Simplify the expression
Calculating the right side:
Δϕ=2π×0.10.4=2π×14=π2
Step 5: State the final answer
The phase difference between the two points situated at a distance of 10 cm on the string is:
Δϕ=π2radians
Summary
The phase difference between the two points is π2 radians.
---
- Speed of the wave (v) = 20 m/s
- Frequency (f) = 50 Hz
- Distance between the two points (Δx) = 10 cm = 0.1 m
The wavelength can be calculated using the formula:
λ=vf
Substituting the known values:
λ=20m/s50Hz=2050=0.4m
The phase difference (Δφ) between two points separated by a distance Δx is given by the formula:
Δϕ=2πΔxλ
Substituting the values we have:
Δϕ=2π×0.1m0.4m
Calculating the right side:
Δϕ=2π×0.10.4=2π×14=π2
The phase difference between the two points situated at a distance of 10 cm on the string is:
Δϕ=π2radians
The phase difference between the two points is π2 radians.
Similar Questions
Small amplitude progressive wave in a stretched string has a speed of 100cm/s.and frequency 100 Hz. The phase difference between two points 2.75 cm apart on the string in radians, is
View SolutionA sound wave of frequency 100 Hz is travelling in air. The speed of sound in air is 350ms−1 (a) By how much is the phase changed at a given point in 2.5 ms ? (b) What is the phase difference at a given instant between two points separated by a distance of 10.0 cm along the direction of propagation ?
View SolutionA progressive wave moves with a velocity of 36m/ s in a medium with a frequency of 200Hz. The phase difference between two particles seperated by a distance of 1 cm is
View SolutionA wave travelling along the length of a string is shown in Fig. 14.4.12. Using the scale on the given axis, find
(i) The amplitude of the wave
(ii) The wavelength of the wave
(iii) If the frequency of the wave is 10 Hz, What is the speed of the wave?
(iv) What is the initial phase of the wave ?
(v) What is the phase difference between two points separated by a distance 10 cm ?
(vi) If this wave is made to travel through water what is the wavelength of the wave, if the speed of, the waves in water is 10 m/s.
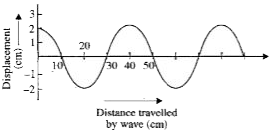
View SolutionThe angular frequency of a particle in a progressive wave in an elastic medium is 100πrads−1 and it is moving with a velocity of 200ms−1 The phase difference between two particles seperated by a distance of 20m is
View SolutionA wave travels at a speed of 0.3 m s−1 and the frequency of wave is 20 Hz. Find the separation between two consecutive compressions.
View SolutionA wave of frequency 20 Hz is propagatinig is space with speed 200 m/s. the phase difference of the two points of wave separated by a distance 5 m is
View SolutionThe phase velocity of a wave of frequency 500 Hz is 400 m/s (i) How far apart are two points 61∘ out of phase? (ii) Calculate the phase difference between two displacements atá certain point at times 10−3 apart
View SolutionA wave of frequency 500 Hz has velocity 360 m/sec. The distance between two nearest points 60∘ out of phase, is
View SolutionA longitudinal wave travels at a speed of 0.3 m s−1 and the frequency of wave is 20 Hz. Find the separation between the two consecutive compressions.
View Solution
