The separation between a node and the next antinode in a vibrating air column is 25 cm. If the speed of sound in air is 340ms−1, find the frequency of vibration of the air column.
The correct Answer is:C, D
To solve the problem, we need to find the frequency of vibration of the air column given the separation between a node and the next antinode and the speed of sound in air.
1. Understanding the Relationship Between Node and Antinode:
- In a vibrating air column, the distance between a node and the next antinode is given by λ4, where λ is the wavelength of the sound wave.
2. Given Data:
- Separation between a node and the next antinode = 25 cm = 0.25 m (convert cm to m).
- Speed of sound in air, v=340m/s.
3. Finding the Wavelength:
- Since the distance between a node and an antinode is λ4, we can express this as:
λ4=0.25m
- To find λ, multiply both sides by 4:
λ=4×0.25=1m
4. Using the Wave Equation:
- The relationship between speed v, frequency f, and wavelength λ is given by:
v=f⋅λ
- Rearranging this equation to solve for frequency f:
f=vλ
5. Substituting the Known Values:
- Now substitute the values of v and λ:
f=340m/s1m=340Hz
6. Final Answer:
- The frequency of vibration of the air column is 340Hz.
- In a vibrating air column, the distance between a node and the next antinode is given by λ4, where λ is the wavelength of the sound wave.
- Separation between a node and the next antinode = 25 cm = 0.25 m (convert cm to m).
- Speed of sound in air, v=340m/s.
- Since the distance between a node and an antinode is λ4, we can express this as:
λ4=0.25m
- To find λ, multiply both sides by 4:
λ=4×0.25=1m
- The relationship between speed v, frequency f, and wavelength λ is given by:
v=f⋅λ
- Rearranging this equation to solve for frequency f:
f=vλ
- Now substitute the values of v and λ:
f=340m/s1m=340Hz
- The frequency of vibration of the air column is 340Hz.
Topper's Solved these Questions
Similar Questions
In a standing wave pattern in a vibrating air column, nodes are formed at a distance of 4.0 cm. If the speed of sound in air is328ms−1 what is the frequency of the source ?
View SolutionConsider the situation shown in figure. The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 40ms−1, find the tension in the wire.
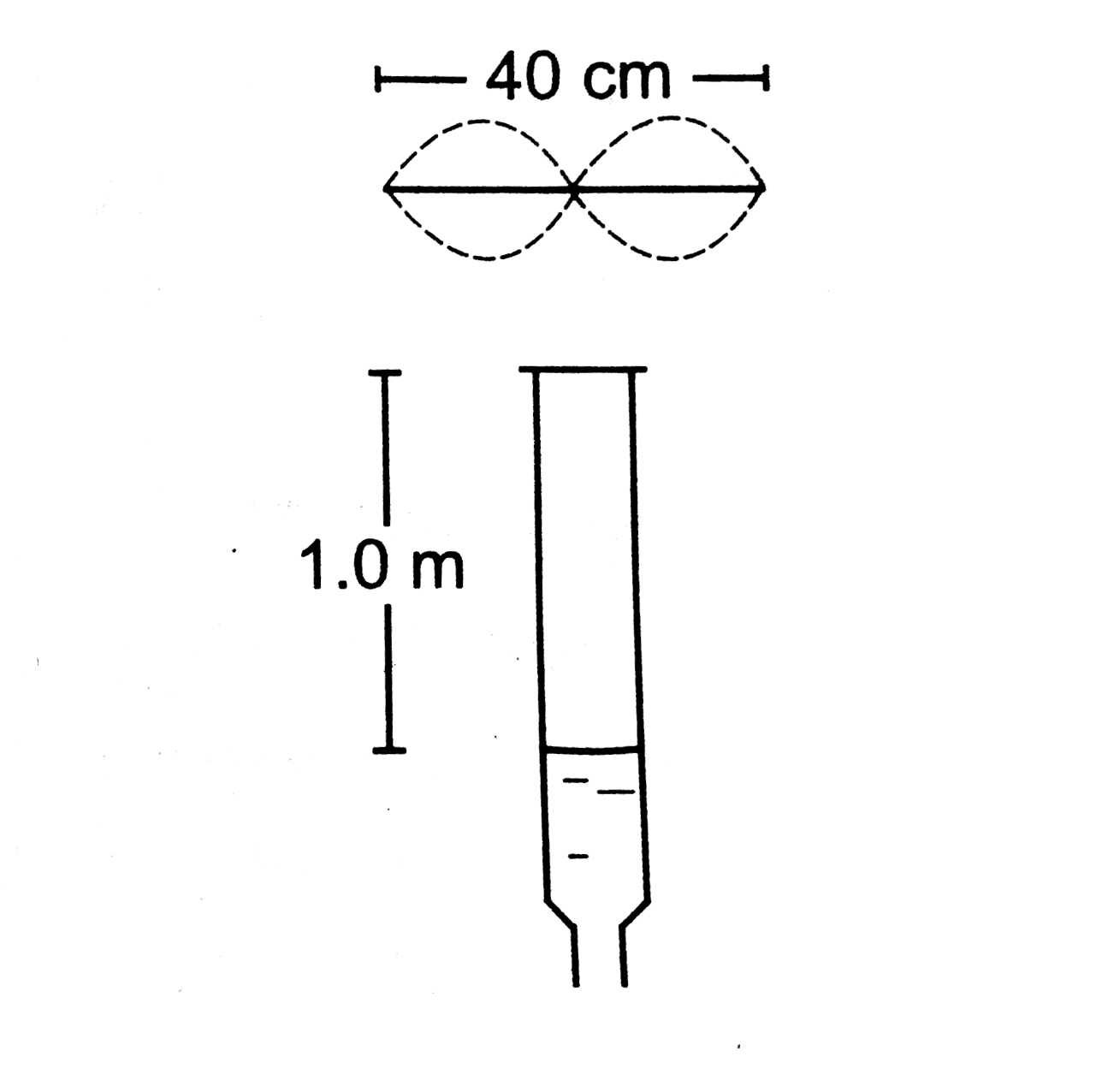 .
.
View SolutionThe air column in a pipe closed at one end is made to vibrate in its second overtone by a tuning fork of frequency 440 Hz. The speed of sound in air is 330 m/s. find the length of air column.
View SolutionA wire of length 40 cm which has a mass of 4 gms oscillates in its second harmonic and sets the air column in the tube to vibrations in its fundamental mode as shown in figure. Assuming speed of sound in air as 340 m/s, find the tension in the wire.

View SolutionA boy fires a gun and another boy at a distance hears the sound of fire 2.5 s after seeing the flash. If speed of sound in air is 340 m s−1, find the distance between the boys.
View SolutionWhat is the fundamental frequency of an open organ pipe of length 42.5 cm, if the velocity of sound in air is 340 m/s?
View SolutionFind the fundamental, first overtone and second overtone frequencies of an open organ pipe of length 20 cm. Speed of sound in air is 340ms−1.
View SolutionA tuning fork makes 256 vibrations per second in air. When the speed of sound is 330m/s, the wavelength of the note emitted is :
View SolutionA wire of length 40cm which has a mass of 4 g oscillates in its second harmonic and sets the air column in the tube to vibrations in its funrations in its fundamental mode as shows in figure. Assuming the speed of sound in air as 340m/s . Find the tension in the wire.

View SolutionIn an organ pipe the distance between the adjacent node is 4cm. Find the frequency of source if speed of sound in air is 336m/s.
View Solution