If the temperature of a uniform rod is slightly increased by Δt, its moment of inertia I about a line parallel to itself will increased by
zero
αIΔt
2αIΔt
3αIΔt.
To solve the problem of how the moment of inertia I of a uniform rod changes when its temperature is slightly increased by ΔT, we can follow these steps:
1. Understanding the Moment of Inertia:
The moment of inertia I of a rod about an axis parallel to itself is given by the formula:
I=∫r2dm
where r is the distance from the axis of rotation to the mass element dm.
2. Effect of Temperature Increase:
When the temperature of the rod increases, the rod undergoes thermal expansion. This means that the length of the rod will increase slightly. However, the mass distribution of the rod remains uniform.
3. Thermal Expansion:
Let’s denote the original length of the rod as L. When the temperature increases by ΔT, the new length L′ can be expressed as:
L′=L+ΔL
where ΔL is the change in length due to thermal expansion.
4. Distance from the Axis:
Since the rod expands uniformly, the distance of any point on the rod from the axis of rotation does not change. The mass elements dm remain at the same distances r from the axis of rotation.
5. Calculating the Change in Moment of Inertia:
Since the distances r of all mass elements from the axis remain unchanged, we can conclude that:
ΔI=I′−I=0
This indicates that the moment of inertia does not change due to the thermal expansion of the rod.
6. Final Conclusion:
Therefore, the increase in the moment of inertia I about a line parallel to itself when the temperature of the uniform rod is slightly increased by ΔT is:
ΔI=0
Final Answer:
The moment of inertia I about a line parallel to itself will not change (i.e., it will increase by 0).
---
The moment of inertia I of a rod about an axis parallel to itself is given by the formula:
I=∫r2dm
where r is the distance from the axis of rotation to the mass element dm.
When the temperature of the rod increases, the rod undergoes thermal expansion. This means that the length of the rod will increase slightly. However, the mass distribution of the rod remains uniform.
Let’s denote the original length of the rod as L. When the temperature increases by ΔT, the new length L′ can be expressed as:
L′=L+ΔL
where ΔL is the change in length due to thermal expansion.
Since the rod expands uniformly, the distance of any point on the rod from the axis of rotation does not change. The mass elements dm remain at the same distances r from the axis of rotation.
Since the distances r of all mass elements from the axis remain unchanged, we can conclude that:
ΔI=I′−I=0
This indicates that the moment of inertia does not change due to the thermal expansion of the rod.
Therefore, the increase in the moment of inertia I about a line parallel to itself when the temperature of the uniform rod is slightly increased by ΔT is:
ΔI=0
The moment of inertia I about a line parallel to itself will not change (i.e., it will increase by 0).
Topper's Solved these Questions
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Exercise
34 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Question for Shor Answer
13 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Worked out Examples
15 Videos
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Question for short Answers
18 Videos
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER
11 Videos
Similar Questions
If the temperature of a uniform rod is slighely increased by Δt its moment of inertia I about perpendicular bisector increases by
View SolutionThe moment of inertia of a rod about its perpendicular bisector is l, when temperature of rod is increased by ΔT, the increase in the moment of inertia of the rod about same axis (γ = temperature coefficient of volume expansion)
View Solution
Knowledge Check
The moment of inertia of a rod about its perpendicular bisector is I . When the temperature of the rod is increased by ΔT , the increase in the moment of inertia of the rod about the same axis is (Here , α is the coefficient of linear expansion of the rod )
AαIΔTB2αIΔTCαIΔT2D2IΔTα
The diameter of a flywheel is increased by 1% . Increase in its moment of interia about the central axis is
View SolutionWhen the temperature of a rod increases from t to r+Δt, its moment of inertia increases from I to I+ΔI. If α is the value of ΔI/I is
View SolutionCalculate the moment of inertia of the given rod about an axis CD.
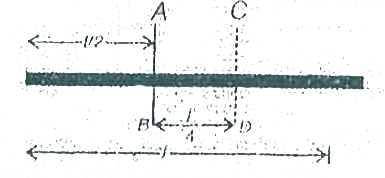
View SolutionCalculate the moment of inertia of the given rod about an axis CD

View SolutionMoment of inertia of a uniform circular disc about a diameter is I. Its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim will be.
View SolutionWhat is the moment of inertia of a uniform circular ring about its diameters ?
View SolutionWhat is the moment of inertia of a uniform circular ring about its diameters ?
View Solution
