A resistance thermometer reads R=20.0Ω,27.5Ω, and 50.0Ω at the ice point (0∘C), the steam point (100∘C) and the zinc point (420∘C) respectively. Assuming that the resistance varies with temperature as RΘ=R0(1+αΘ+βΘ2) , find the values of R0, α and β. Here Θ represents the temperature on Celsius scale.
To solve the problem, we will follow these steps:
Step 1: Set up the equations based on the given data
We know that the resistance RΘ varies with temperature Θ according to the formula:
RΘ=R0(1+αΘ+βΘ2)
We have three data points:
1. At the ice point (0°C), R0=20.0Ω
2. At the steam point (100°C), R100=27.5Ω
3. At the zinc point (420°C), R420=50.0Ω
Step 2: Substitute the known values into the equation
1. For Θ=0:
20=R0(1+α⋅0+β⋅02)⟹20=R0
Thus, R0=20Ω.
2. For Θ=100:
27.5=20(1+100α+10000β)
Simplifying this gives:
27.5/20−1=100α+10000β
0.375=100α+10000β(Equation 1)
3. For Θ=420:
50=20(1+420α+176400β)
Simplifying gives:
50/20−1=420α+176400β
1.5=420α+176400β(Equation 2)
Step 3: Solve the equations
Now we have two equations:
1. 100α+10000β=0.375 (Equation 1)
2. 420α+176400β=1.5 (Equation 2)
We can solve these equations simultaneously.
From Equation 1, we can express α in terms of β:
α=0.375−10000β100
Substituting this into Equation 2:
420(0.375−10000β100)+176400β=1.5
Multiplying through by 100 to eliminate the fraction:
420(0.375−10000β)+17640000β=150
157.5−4200000β+17640000β=150
Combining like terms:
(17640000−4200000)β=150−157.5
13440000β=−7.5
β=−7.513440000≈−5.6×10−7°C−2
Step 4: Substitute β back to find α
Substituting β back into Equation 1 to find α:
100α+10000(−5.6×10−7)=0.375
100α−5.6×10−3=0.375
100α=0.375+5.6×10−3
100α=0.3806
α=0.3806100≈3.806×10−3°C−1
Final Values
Thus, we have:
- R0=20.0Ω
- α≈3.806×10−3°C−1
- β≈−5.6×10−7°C−2
1. At the ice point (0°C), R0=20.0Ω
2. At the steam point (100°C), R100=27.5Ω
3. At the zinc point (420°C), R420=50.0Ω
20=R0(1+α⋅0+β⋅02)⟹20=R0
Thus, R0=20Ω.
27.5=20(1+100α+10000β)
Simplifying this gives:
27.5/20−1=100α+10000β
0.375=100α+10000β(Equation 1)
50=20(1+420α+176400β)
Simplifying gives:
50/20−1=420α+176400β
1.5=420α+176400β(Equation 2)
1. 100α+10000β=0.375 (Equation 1)
2. 420α+176400β=1.5 (Equation 2)
α=0.375−10000β100
420(0.375−10000β100)+176400β=1.5
Multiplying through by 100 to eliminate the fraction:
420(0.375−10000β)+17640000β=150
157.5−4200000β+17640000β=150
Combining like terms:
(17640000−4200000)β=150−157.5
13440000β=−7.5
β=−7.513440000≈−5.6×10−7°C−2
100α+10000(−5.6×10−7)=0.375
100α−5.6×10−3=0.375
100α=0.375+5.6×10−3
100α=0.3806
α=0.3806100≈3.806×10−3°C−1
- R0=20.0Ω
- α≈3.806×10−3°C−1
- β≈−5.6×10−7°C−2
Topper's Solved these Questions
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Question for Shor Answer
13 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 1
12 Videos
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Question for short Answers
18 Videos
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER
11 Videos
Similar Questions
Resistance of a resistor at temperature t∘C is Rt=R0(1+αt+βt2), where R0 is the resistance at 0∘C. The temperature coefficient of resistance at temperature t∘C is
View SolutionA platinum resistance thermometer reads 00 and 1000 at the ice point and boiling point of water respectively. The resistance of a platinum wire varies with Celsius temperature θ as Rt=R0(1+αθ+βθ2), where α=3.8×10−3^0C−1 and β=−5.6×10−7^0C−2. What will be the reading of this thermometer if it is placed in a liquid bath maintained at 500C?
View SolutionThe resistance of a conductor is 5Ω at 50∘C and 6Ω at 100∘C. The resistance at 0∘C is
View SolutionA platinum resistance thermometer reads 0∘ when its resistance is 80Ω and 100∘ when its resistance is 90Ω. Find the temperature at the platinum scale at which the resistance is 86Ω.
View SolutionThe resistance in the two arms of the meter bridge are 5Ω and RΩ, respectively. When the resistance R is shunted with an equal resistance, the new balance point is 1.6l1.
The resistance R is
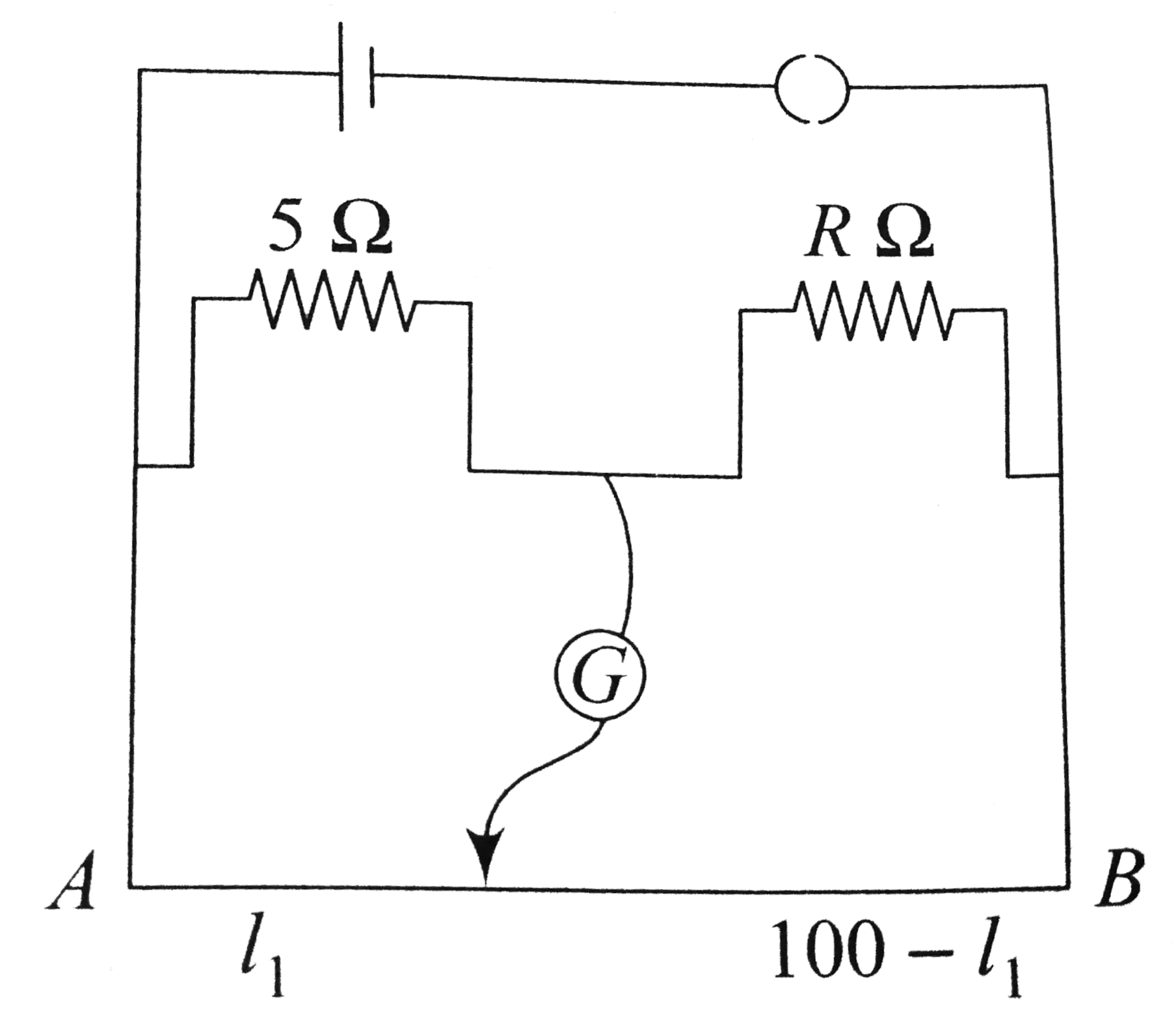
View SolutionThe resistance in the two arms of the meter bridge are 5Ω and RΩ, respectively. When the resistance R is shunted with an equal resistance, the new balance point is 1.6l1.
The resistance R is

View SolutionIn the given circuit current flowing through the resistance 20Ω is 0.3A, while the ammeter reads 0.8 A. What is the value of R1

View SolutionIn the given circuit current flowing through the resistance 20Ω is 0.3A, while the ammeter reads 0.8 A. What is the value of R1

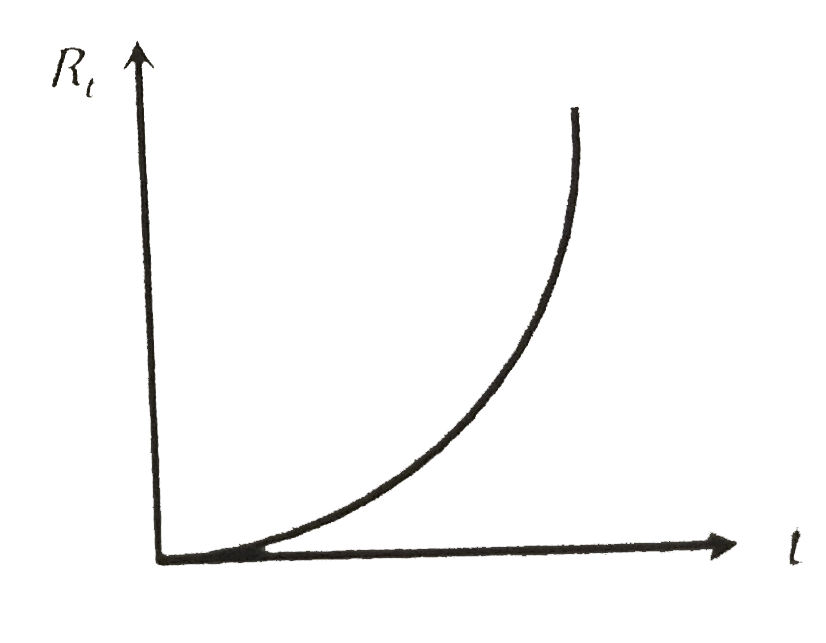
View SolutionThe resistance R of a conductor varies with temperature t as shown in the figure. If the variation is represented by Rt=R0[1+αt+βt2], then
View SolutionA platinum resistance thermometer reads 0∘C when its resistance is 80Ωand100∘C when its resistance is 90Ω. Find the temperature at which the resistance is 86Ω.
View Solution
