Two steel rods and an aluminum rod of equal length l0 and equal cross section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 0∘C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminum and steel are αaandαs respectively. Young's modulus of aluminum is Ya and of steel is Ys.
Let the initial length of the system at 0∘C
=l0
When temperature changes by θ
Final length of the steel at system temperature.
So, strain of the system=l−(l0)l0
Steel
Aluminium
Steel
But the total strain of the system
= total stress of system/ total Young's modulus of system
Now, total stress due to two steel rod
+ stress due to aluminium
=(γsαsθ)+(γsαsθ)+((γAl)(αAl)θ)
=(2γsαsθ)+(γAlαAlθ)
Now Young's modulus system
=γs+γs+γAl=(2γs+γAl
∴Stra∈ofsystem=(2γsαsθ)+γAlαAlθ2γs+γAl
l−ll0=(2γsαsθ)+(γAlαAlθ)2γs+γAl
l= (l_0)[ 1+((2gamma_s alpha_s theta)+(2gamma_(Al) alpha_(Al) theta) / (2 gamma_s+ gamma_(Al))
Similar Questions
Two steel rods and an aluminium rod of equal length l0 and equal cross- section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 0∘C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminium and steel are αa and αs respectively. Young's modulus of aluminium is Ya and of steel is Ys.
View SolutionA uniform cylindrical rod of length L and cross-sectional area by forces as shown in figure.
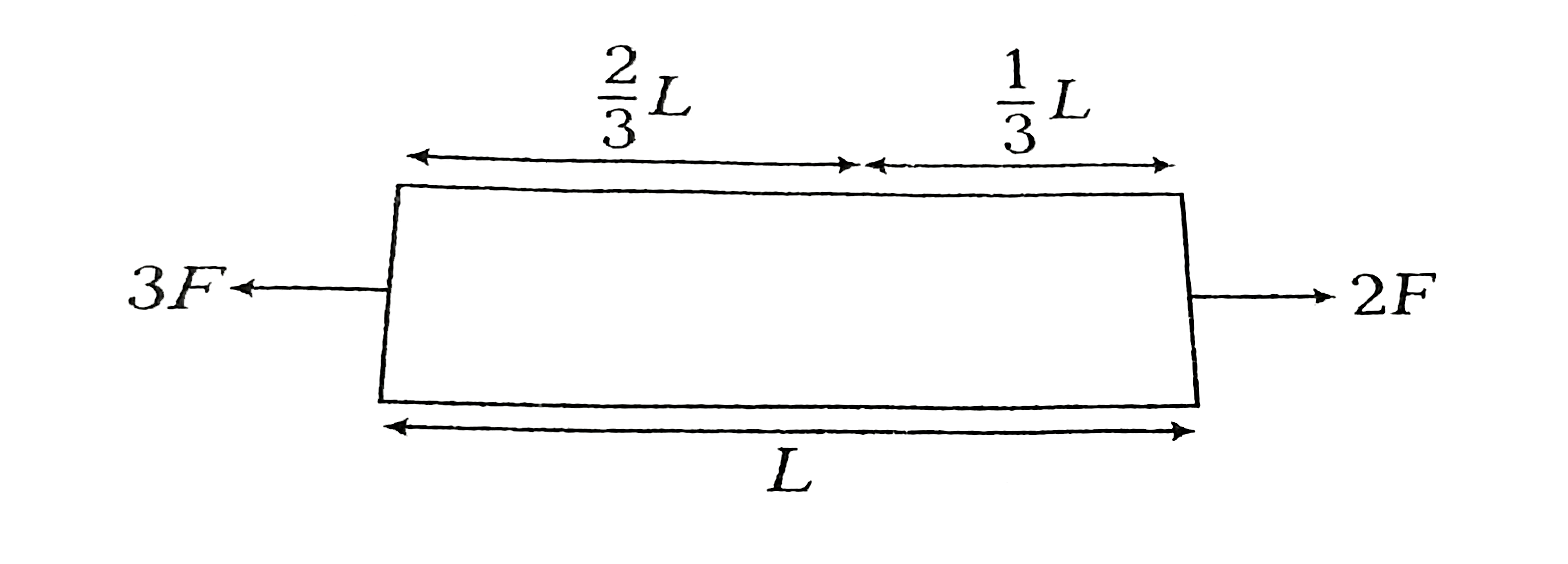
The elongation produced in the rod isView SolutionA steel rod is clamped at its two ends and rests on a fixed horizontal base. The rod is unstrained at 20∘C. Find the longitudinal strain developed in the rod if the temperature rises to 50∘C. Coefficient of linear expansion of steel =1.2×10−5C−1.
View Solution
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will beView SolutionA steel rod is clamped at its two ends and rests on a fixes horizontal base. The rod is unstrained at 20∘C. Find the longitudinal strain developed in the rod if the temperature rises to 50∘C. Coefficient of linear expansion of steel =1.2×10−5∘C−1.
View SolutionA steel rod is clamped at its two ends and rests on a fixes horizontal base. The rod is unstrained at 20∘C. Find the longitudinal strain developed in the rod if the temperature rises to 50∘C. Coefficient of linear expansion of steel =1.2×10−5∘C−1.
View SolutionThere are two rods of length l1 and l2 and coefficient of linear expansions are α1 and α2 respectively.
Find equivalent coefficient of thermal expansion for their combination in series.View SolutionTwo rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_227_Q01.png)
If temperature of system is increased by ΔT then junction will not shift if -View SolutionTwo rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_229_Q01.png)
If temperature of system is increased by ΔT then shifting in junction if junction if Y1α1>Y2α2 is given by -View SolutionTwo metallic rods of length l and 3l have coefficient of linear expansion α and 3α respectively. The coefficient of linear expansion ofr their series combinations, is
View Solution