In a calorimeter, the beat given by the bot object is assumed to be equal to the beat taken by the cold object. Does it mean that beat of the two object taken togather remain constant?
Step by step video & image solution for In a calorimeter, the beat given by the bot object is assumed to be equal to the beat taken by the cold object. Does it mean that beat of the two object taken togather remain constant? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
The weight of an object is 90 kg at the surface of the earth. If it is taken to a height equal to half of the radius of the earth, then its weight will become
View SolutionLet ω be the angular velocity of the earth's rotation about its axis. Assume that the acceleration due to gravity on the earth's surface has the same value at the equator and the poles. An object weighed at the equator gives the same reading as a reading taken at a depth d below earth's surface at a pole (d<<R). the value of d is-
View Solution
Knowledge Check
- Question 1 - Select One
Assertion : The average speed of an object is greater than or equal to the magnitude of the average velocity over a given time interval.
Reason : The two are equal only if the path length is equal to the magnitude of displacement.AIf both assertion and reason are trure and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanations of assertion.CIf assertion is true but reason is false.DIf both assertion and reason is false - Question 2 - Select One
Which of the following expressions given the number of permulations of 15 objects taken 5 at a time?
A15(5)B(15 - 5)!C15!5!D15!(15−5)!
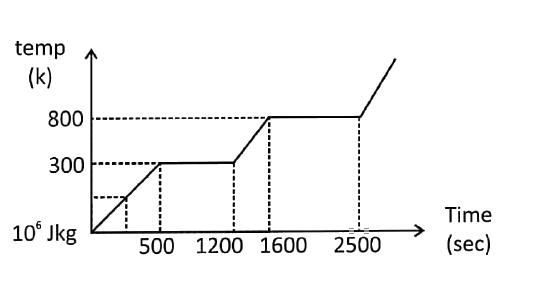
A heating curve has been plotted for a solid object as shown in the figure. If the mass of the object is 100g, then latent heat of vaporization for the material of the object is [Given, power supplied to the object is constant and equal to 1 kW]
 View Solution
View Solution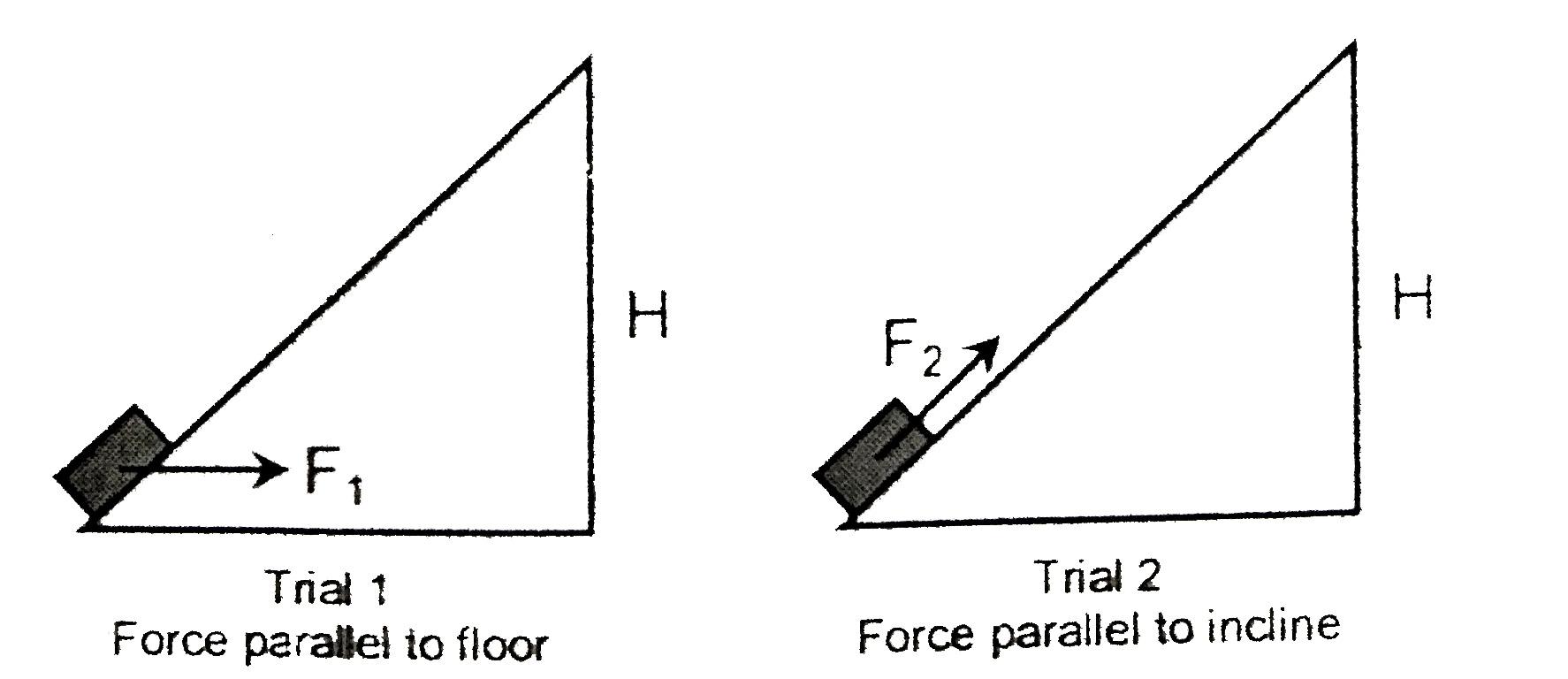
An object of mass M starts from rest at the bottom of a fixed incline of height H. A person decides to push the object up the incline in one of two ways with an applied force shown in the diagram. In each of the trials, the object reaches the top of the incline with speed V. How would the work done by the person on the block compare for the two trials? Assume the same constant non-zero coefficient of kinetic friction between the incline and the object for both trials.View SolutionTwo metallic plate A and B , each of area 5×10−4m2, are placed parallel to each at a separation of 1cm plate B carries a positive charge of 33.7×10−12C A monocharonatic beam of light , with photoes of energy 5eV each , starts falling on plate A at t=0 so that 1016 photons fall on it per square meter per second. Assume that one photoelectron is emitted for every 106 incident photons fall on it per square meter per second. Also assume that all the emitted photoelectrons are collected by plate B and the work function of plate A remain constant at the value 2eV Determine
(a) the number of photoelectrons emitted up to i=10s,
(b) the magnitude of the electron field between the plate A and B at i=10s,and
(c ) the kinetic energy of the most energotic photoelectrons emitted at i=10s whenit reaches plate B
Negilect the time taken by the photoelectrons to reach plate B Take ε0=8.85×10−12C2N−m2View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
If buoyant force were also taken into account then value of terminal speed would haveView SolutionAn object of density σ(<ρ) is dropped from rest at a height h into a liquid of density ρ kept in a tall vertical cylindrical container. Neglect all dissipative effects and assume that there is no spilling of the liquid.
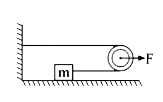
The time taken by the object to reach the starting point (from which it is dropped) isView SolutionIn the given figure the pulley is assumed massless and frictionless. If the friction force on the object of mass m is f, then its acceleration in terms of the force F will be equal to :
 View Solution
View Solution

