A gas is enclosed in a cylindrical vessel fitted with a frictionless piston.the gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10cm. Find the increase in the internal energy of the gas, the area of cross section of the cylinder=4cm2 and the atmospheric pressure =100kPa.
To solve the problem step by step, we will use the first law of thermodynamics and the given data to find the increase in the internal energy of the gas.
Step 1: Understand the given data
- Heat supplied to the gas (Q) = 10 J
- Displacement of the piston (d) = 10 cm = 0.1 m
- Area of cross-section of the cylinder (A) = 4 cm² = 4 × 10⁻⁴ m²
- Atmospheric pressure (P) = 100 kPa = 100 × 10³ Pa
Step 2: Calculate the change in volume (ΔV)
The change in volume (ΔV) can be calculated using the formula:
ΔV=A×d
Substituting the values:
ΔV=(4×10−4m2)×(0.1m)=4×10−5m3
Step 3: Calculate the work done (W)
The work done by the gas when the piston moves against the atmospheric pressure can be calculated using the formula:
W=P×ΔV
Substituting the values:
W=(100×103Pa)×(4×10−5m3)=4J
Step 4: Apply the first law of thermodynamics
The first law of thermodynamics states:
Q=W+ΔU
Where:
- Q = heat supplied
- W = work done
- ΔU = change in internal energy
Rearranging the equation to find the change in internal energy (ΔU):
ΔU=Q−W
Substituting the values:
ΔU=10J−4J=6J
Final Answer
The increase in the internal energy of the gas is 6 J.
---
- Heat supplied to the gas (Q) = 10 J
- Displacement of the piston (d) = 10 cm = 0.1 m
- Area of cross-section of the cylinder (A) = 4 cm² = 4 × 10⁻⁴ m²
- Atmospheric pressure (P) = 100 kPa = 100 × 10³ Pa
The change in volume (ΔV) can be calculated using the formula:
ΔV=A×d
Substituting the values:
ΔV=(4×10−4m2)×(0.1m)=4×10−5m3
The work done by the gas when the piston moves against the atmospheric pressure can be calculated using the formula:
W=P×ΔV
Substituting the values:
W=(100×103Pa)×(4×10−5m3)=4J
The first law of thermodynamics states:
Q=W+ΔU
Where:
- Q = heat supplied
- W = work done
- ΔU = change in internal energy
ΔU=Q−W
Substituting the values:
ΔU=10J−4J=6J
The increase in the internal energy of the gas is 6 J.
Topper's Solved these Questions
Similar Questions
In given figure, gas is slowely heated for sometime. During the process, the increases in internal energy of the gas is 10J and the piston is found to move out by 25cm, then find the amount of heat supplied. The area of cross-section of cylinder =40cm2 and atmospheric pressure 100kPa
View SolutionA simple of gas present in a cylinder fitted with a frictionless piston expands against constant pressure of 1atm from a volume fo 2L to 12L. During the process, it absorbs 600J of heat from the surroundings. Calculate the change in internal energy of the system.
View SolutionA gas is contained in a vessel fitted with a movable piston. The container is placed on a stove. A total of 100 cal of heat is given to the gas and the gas does 40 J of work in the expansion resulting from heating. Calculate the increase in internal energy in the process.
View SolutionA gas is at 1 atm pressure with a volume 800cm3. When 100J of heat is supplied to the gas, it expands to 1L at constant pressure. The change in its internal energy is
View SolutionA gas is at 1 atm pressure with a volume 800cm3. When 100J of heat is supplied to the gas, it expands to 1L at constant pressure. The change in its internal energy is
View SolutionTwo moles of nitrogen gas is kept in a cylinder of cross-section area 10cm3. The cylinder is closed by a light frictionless piston. Now the gas is slowly heated such that the displacement of piston during process is 50cm, find the rise in temperature of gas when 200J of heat is added in it. (Atmospheric pressure =100kPa,R=25/3J/mol−K)
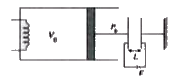
View SolutionAn ideal gas is enclosed in a cylinder fitted with a frictionless piston. The piston is connected with a light rod to one plate of capacitor whose other plate is fixed as shown. Initially volume of the gas inside the cylinder is V0 Atmospheric pressure is P0 separation between the plates is L, area of the piston as well as of the capacitor plates is A and emf of battery is ε . A heater supplies heat to the gas so that pressure of the gas is given as P=P0−nε0ε2L2 when piston is displaced by a distance L2 . Find value of n.
View Solution500cm3 of a sample of an ideal gas is compressed by an average pressure of 0.1atm of 250cm3. During this process, 10J of heat flows out to the surroundings. Calculate the change in internal enegry of the system.
View Solution500cm3 of a sample of an ideal gas is compressed by an average pressure of 0.1atm of 250cm3. During this process, 10J of heat flows out to the surroundings. Calculate the change in internal enegry of the system.
View SolutionDuring a process ideal gas expands to compress the spring such that 10kJ energy is stored in the spring and 2kJ heat is released from gas to surrounding find the change in internal energy of gas
View Solution
