Consider two particles A and B having equal charges
. and placed at some distance. The particle A is slightly
. displaced towards B. Does the force on B increase as
. soon as th particle A is displaced? Does the force on
. the particle A increase as soon as it is displaced?
To solve the problem, we need to analyze the forces acting on two charged particles A and B when particle A is slightly displaced towards particle B.
1. Identify the Initial Setup:
- Let the charges of particles A and B be Q each.
- Let the initial distance between particles A and B be x.
2. Calculate the Initial Forces:
- According to Coulomb's Law, the force FAB exerted on particle A by particle B is given by:
FAB=kQ2x2
- Similarly, the force FBA exerted on particle B by particle A is:
FBA=kQ2x2
- Both forces are equal in magnitude and opposite in direction.
3. Displacement of Particle A:
- Now, particle A is displaced slightly towards particle B, reducing the distance between them. Let’s denote the new distance as D=x−d, where d is the small displacement towards B.
4. Calculate the New Forces:
- The new force F′AB on particle A due to particle B after the displacement is:
F′AB=kQ2(x−d)2
- Similarly, the new force F′BA on particle B due to particle A is:
F′BA=kQ2(x−d)2
5. Analyze the Change in Forces:
- Since the distance between the charges has decreased (from x to x−d), we can see that:
(x−d)2<x2
- Therefore, the new forces F′AB and F′BA are greater than the initial forces FAB and FBA:
F′AB>FABandF′BA>FBA
6. Conclusion:
- The force on particle B increases as soon as particle A is displaced towards it.
- Similarly, the force on particle A also increases due to the same reason.
Final Answer:
Yes, the force on particle B increases as soon as particle A is displaced, and the force on particle A also increases as soon as it is displaced.
- Let the charges of particles A and B be Q each.
- Let the initial distance between particles A and B be x.
- According to Coulomb's Law, the force FAB exerted on particle A by particle B is given by:
FAB=kQ2x2
- Similarly, the force FBA exerted on particle B by particle A is:
FBA=kQ2x2
- Both forces are equal in magnitude and opposite in direction.
- Now, particle A is displaced slightly towards particle B, reducing the distance between them. Let’s denote the new distance as D=x−d, where d is the small displacement towards B.
- The new force F′AB on particle A due to particle B after the displacement is:
F′AB=kQ2(x−d)2
- Similarly, the new force F′BA on particle B due to particle A is:
F′BA=kQ2(x−d)2
- Since the distance between the charges has decreased (from x to x−d), we can see that:
(x−d)2<x2
- Therefore, the new forces F′AB and F′BA are greater than the initial forces FAB and FBA:
F′AB>FABandF′BA>FBA
- The force on particle B increases as soon as particle A is displaced towards it.
- Similarly, the force on particle A also increases due to the same reason.
Yes, the force on particle B increases as soon as particle A is displaced, and the force on particle A also increases as soon as it is displaced.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 1
9 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
Two particles A and B having equal charges are placed at distance d apart. A third charged particle placed on the perpendicular bisector at a distance x will experience the maximum Coulomb’s force when :
View SolutionTwo particles having charge Q1 and Q2 , when kept at a certain distance exert a force F on each other . If the distance between the two particles is reduced to half and the charge on each particle is doubled , the force between the particles would be
View Solution
Knowledge Check
Two particles have unequal charges, one is +q and the other is -2q. The strength of the electrostatic force between these two stationary particles is equal to F. what happens of F if the distance between the particles is halved?
AIt decreases by a factor of 4Bit decreases by a factor of 2.Cit remains the same.Dit increases by a factor of 4.
If distance coverd by a particle is zero , what can be its displacement ?
View SolutionTwo particles A and B having charges q and 2q respectively are placed on a smooth table with a separation d. A third particle C is to be clamped on the table in such a way that the particles A and B remain at rest on the table under electrical forces. What should be the charge on C and where should it clamped?
View SolutionIf the displacement of a particle is zero, then distance covered by it
View SolutionIf the displacement of a particle is zero, then distance covered by it
View SolutionForce F on a particle moving in a straight line varies with distance d as shown in the figure. The work done on the particle during its displacement of 12m is
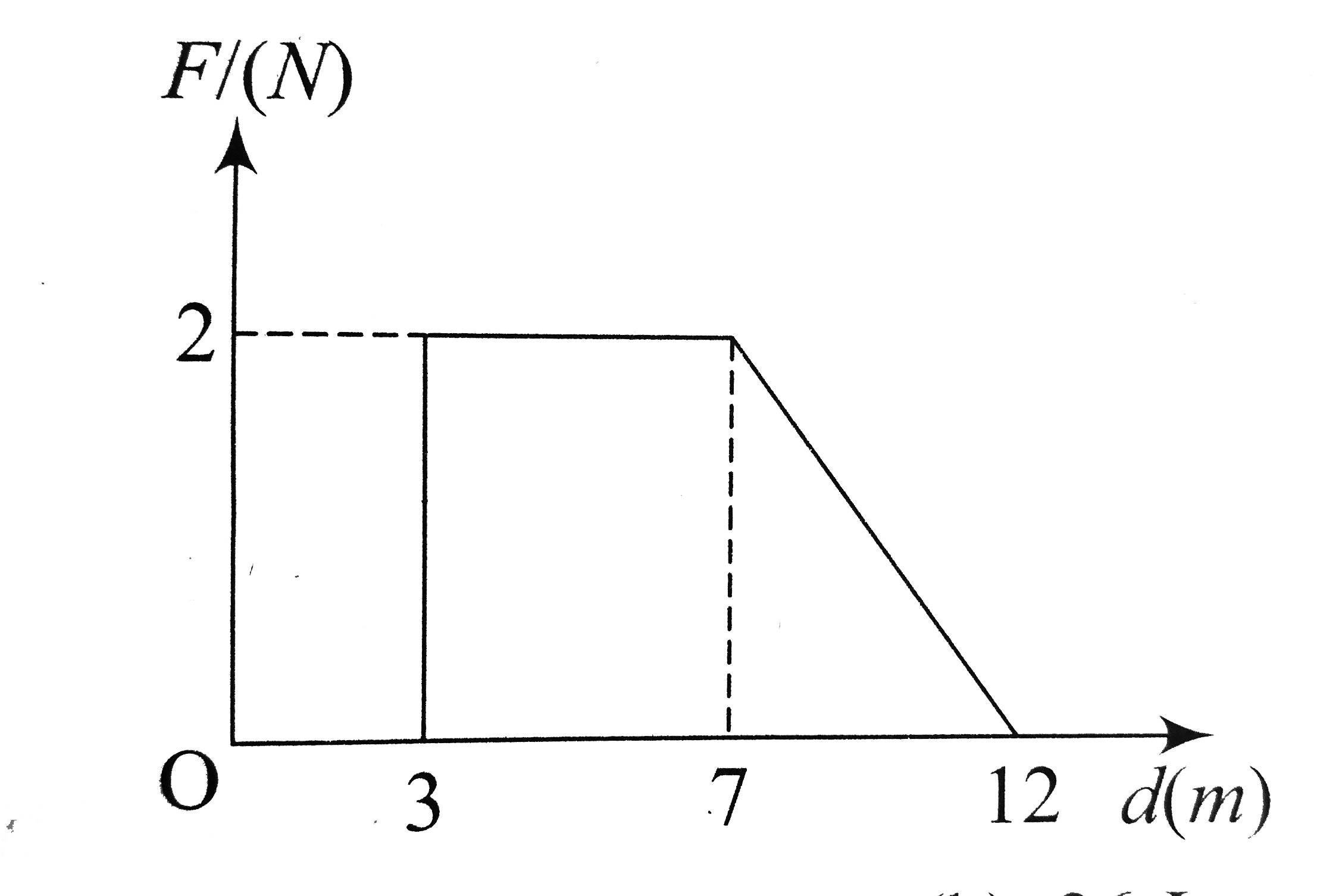
View SolutionA particle travels from A to B path shown in figure, then the displacement of particle is :
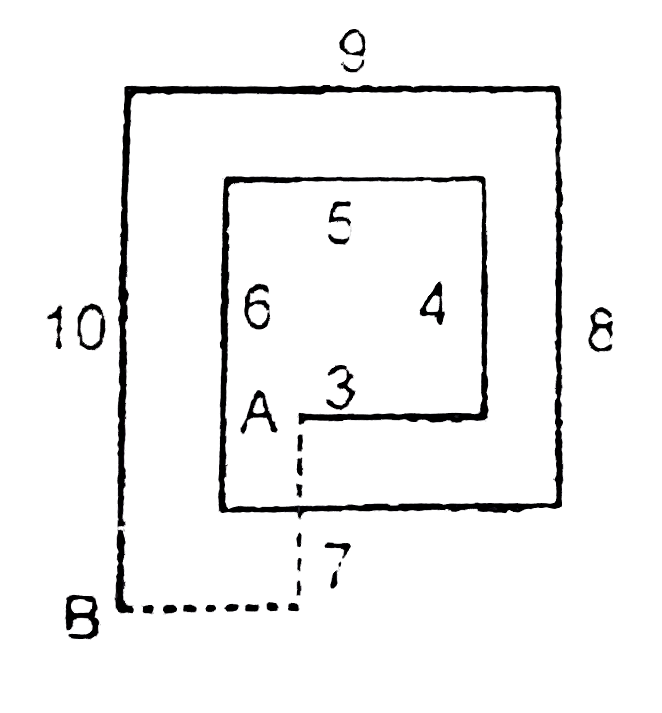 .
.
View SolutionTwo particles A and B , each carrying charge Q are held fixed with a separation D between them. A particle C having mass m and charge q is kept at the middle point of the line AB. If particle C is displaced through a distance x along the line AB. What will be the time period of the oscillations.
View Solution