The electric field and the electric potential at a point are E and V respectively. Give the relationship between E and V
If E =0, V respectivley.
If V = 0, E must be zero.
IfE≠0, V cannot be zero.
If V≠0, E cannot be zero.
To find the relationship between the electric field (E) and the electric potential (V) at a point, we can follow these steps:
Step 1: Understanding Electric Field and Electric Potential
Electric field (E) is a measure of the force experienced by a unit positive charge placed in the field. Electric potential (V), on the other hand, is the amount of work done in bringing a unit positive charge from infinity to a point in the field without acceleration.
Step 2: Relationship Definition
The relationship between electric field and electric potential can be derived from the definition of electric field. The electric field is defined as the negative gradient (or spatial derivative) of the electric potential.
Step 3: Mathematical Representation
In mathematical terms, this relationship can be expressed as:
E=−dVdx
where:
- E is the electric field,
- V is the electric potential,
- x is the position in space.
Step 4: Interpretation
This equation indicates that the electric field is directed from regions of higher potential to regions of lower potential. The negative sign signifies that as you move in the direction of the electric field, the electric potential decreases.
Conclusion
Thus, the relationship between electric field (E) and electric potential (V) is given by:
E=−dVdx
---
Electric field (E) is a measure of the force experienced by a unit positive charge placed in the field. Electric potential (V), on the other hand, is the amount of work done in bringing a unit positive charge from infinity to a point in the field without acceleration.
The relationship between electric field and electric potential can be derived from the definition of electric field. The electric field is defined as the negative gradient (or spatial derivative) of the electric potential.
In mathematical terms, this relationship can be expressed as:
E=−dVdx
where:
- E is the electric field,
- V is the electric potential,
- x is the position in space.
This equation indicates that the electric field is directed from regions of higher potential to regions of lower potential. The negative sign signifies that as you move in the direction of the electric field, the electric potential decreases.
Thus, the relationship between electric field (E) and electric potential (V) is given by:
E=−dVdx
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 1
9 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
Figure shows the electric lines of force emerging from a charged body. If the electric field atA and B are EA and EB respectively and if the displacement between A and B is r then

View SolutionFigure shows the electric lines of force emerging from a charged body. If the electric field atA and B are EA and EB respectively and if the displacement between A and B is r then

View SolutionA charge +Q at A as shown produces electric field E and electric potential V at D. If we now put charges −3Q and +Q at B and C, respectively, then the electric field and potential at D will be
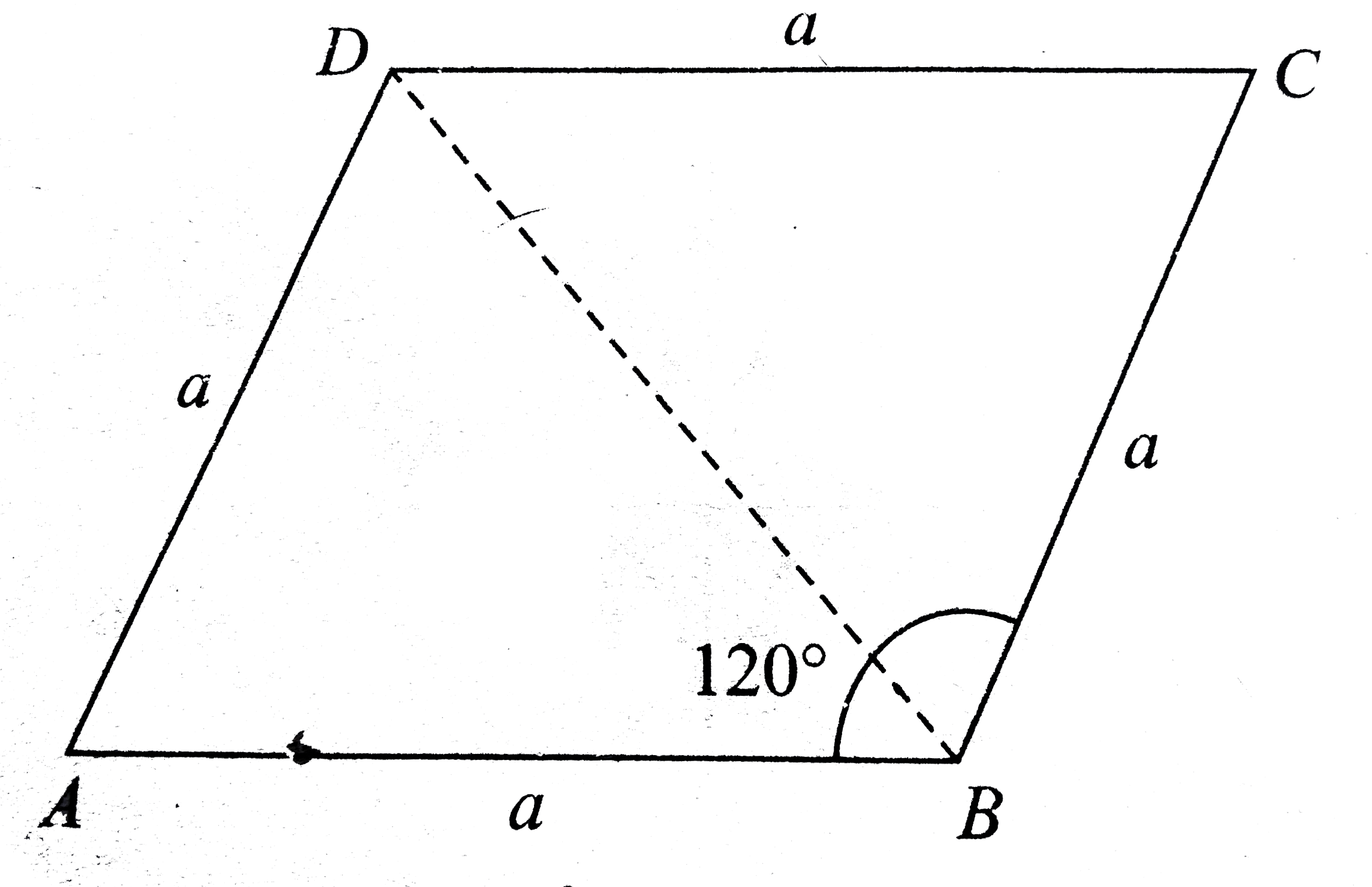 .
.
View SolutionCharges are placed on the vertices of a square as shown. Let E r be the electric field and V the potential at the centre. If the charges on A and B are interchanged with those on D and C respectively, then :-

View SolutionThe figure shows the electric lines of force emerging from a charged body. If the electric fields at A and EA and EB respectively and if the the distance between A anf B is r, then

View SolutionShown a part of an electric circuit, The potentials at the points a,b,and c are 30V,12V,and 2V respectively.Find the currents through the three resistors.
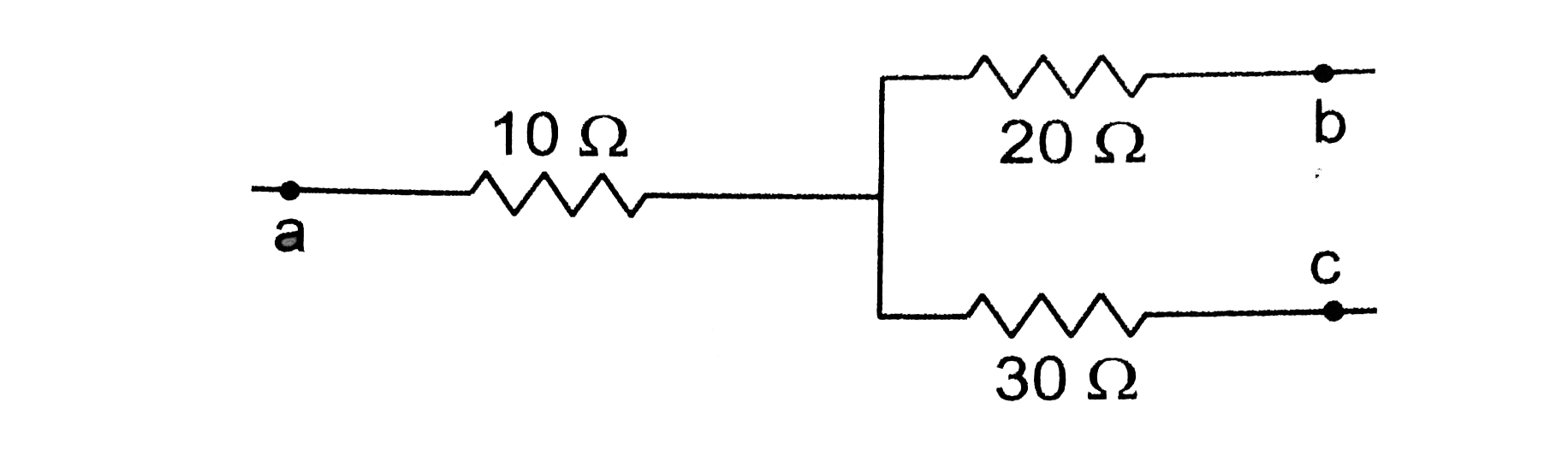
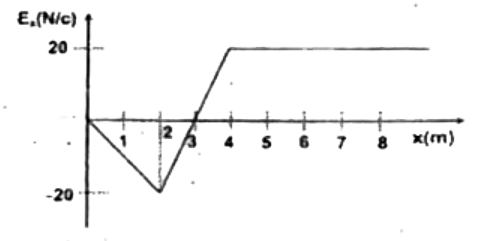
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in the figure. They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V. The value of x for which potential is zero is
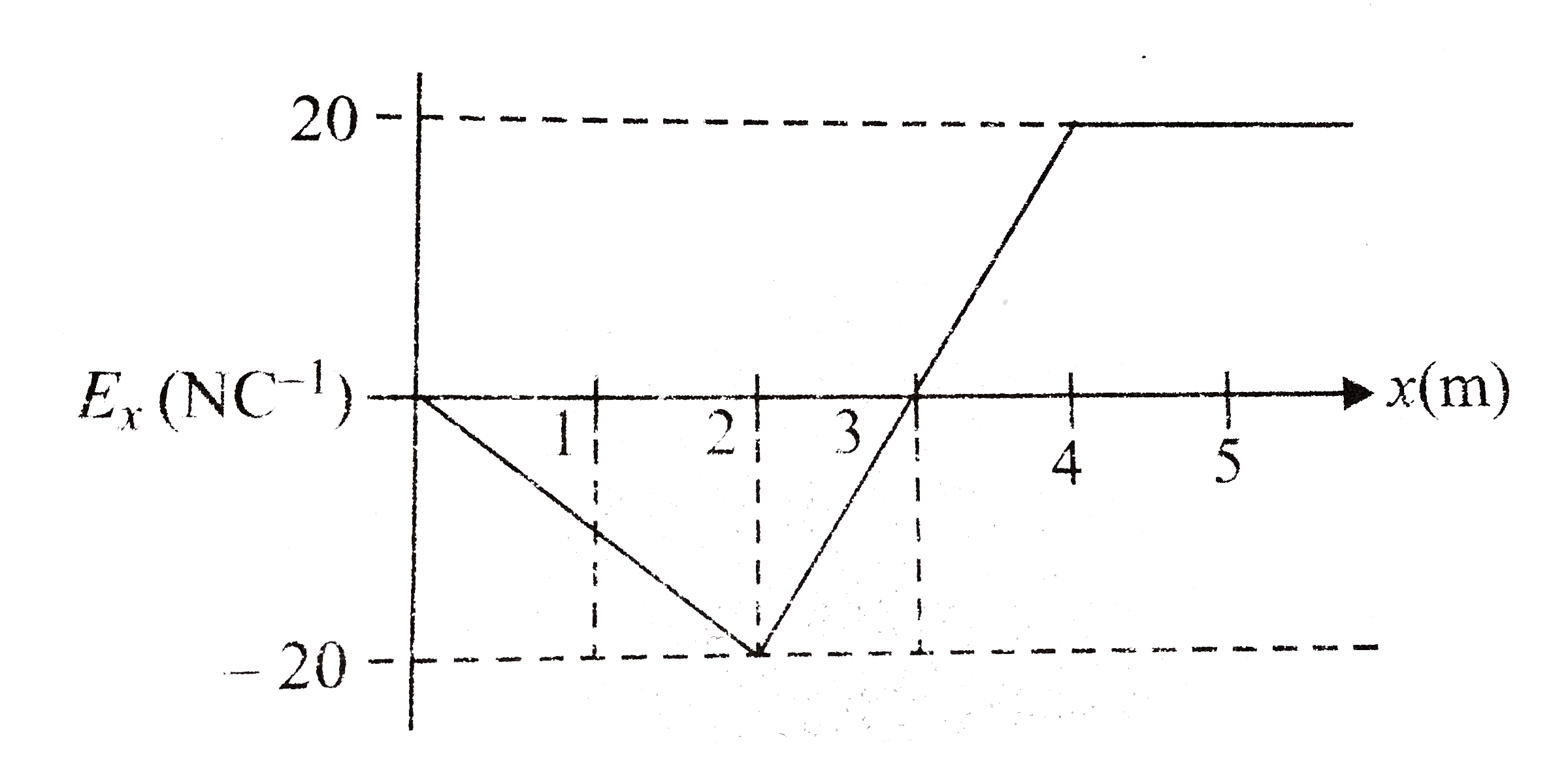
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
View SolutionFigure shows electric lines of force. If Ex and Ey are the magnitudes of electric field at points x and y respectively, then
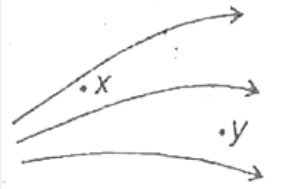
View SolutionIn a certain region of space the electric potential V is known to be constant. Is the electric field in this region (a) positive (b) zero ,or (c ) negative ?
View Solution
