A block of mass m having a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k as shown in figure(29.E1) . A horizontal electric field E parallel to the spring is switched on. Find the amplitude of the resulting SHM of the block.
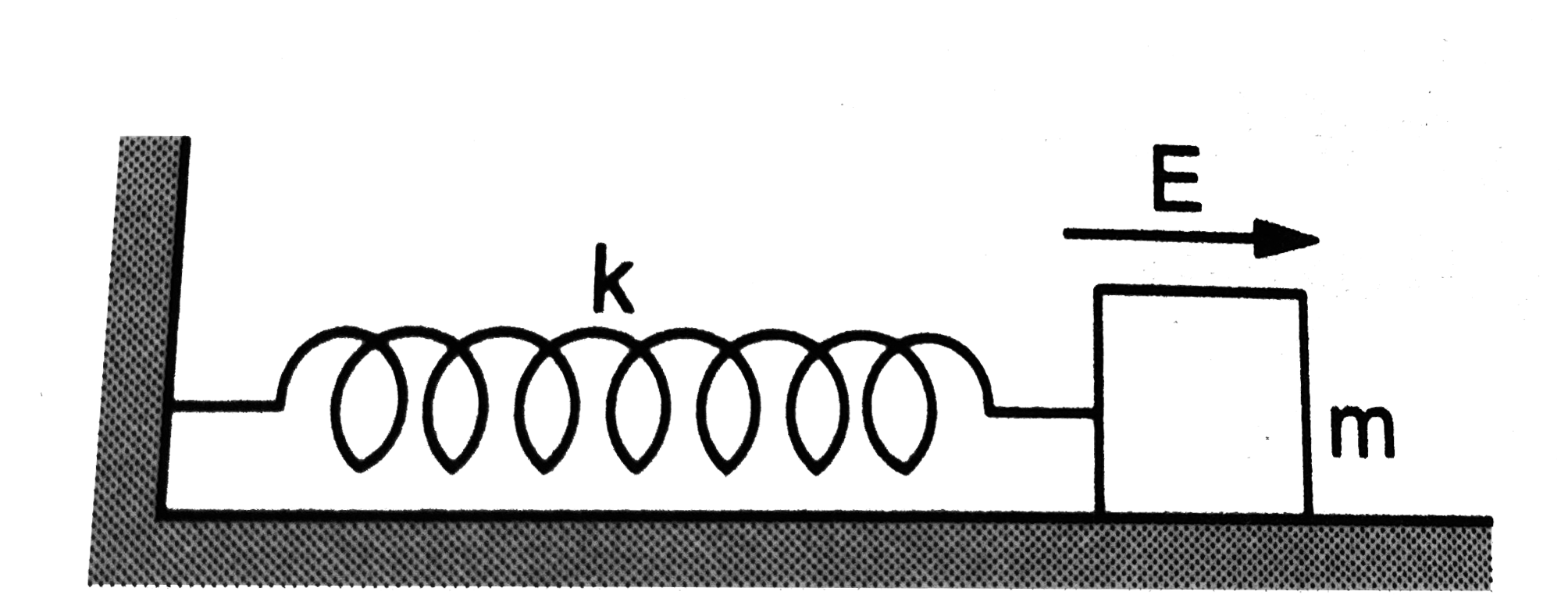
F=qE,F−kx[wherexamplitude]
qE=−kx
orx=qEk
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 1
9 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - worked out Examples
19 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
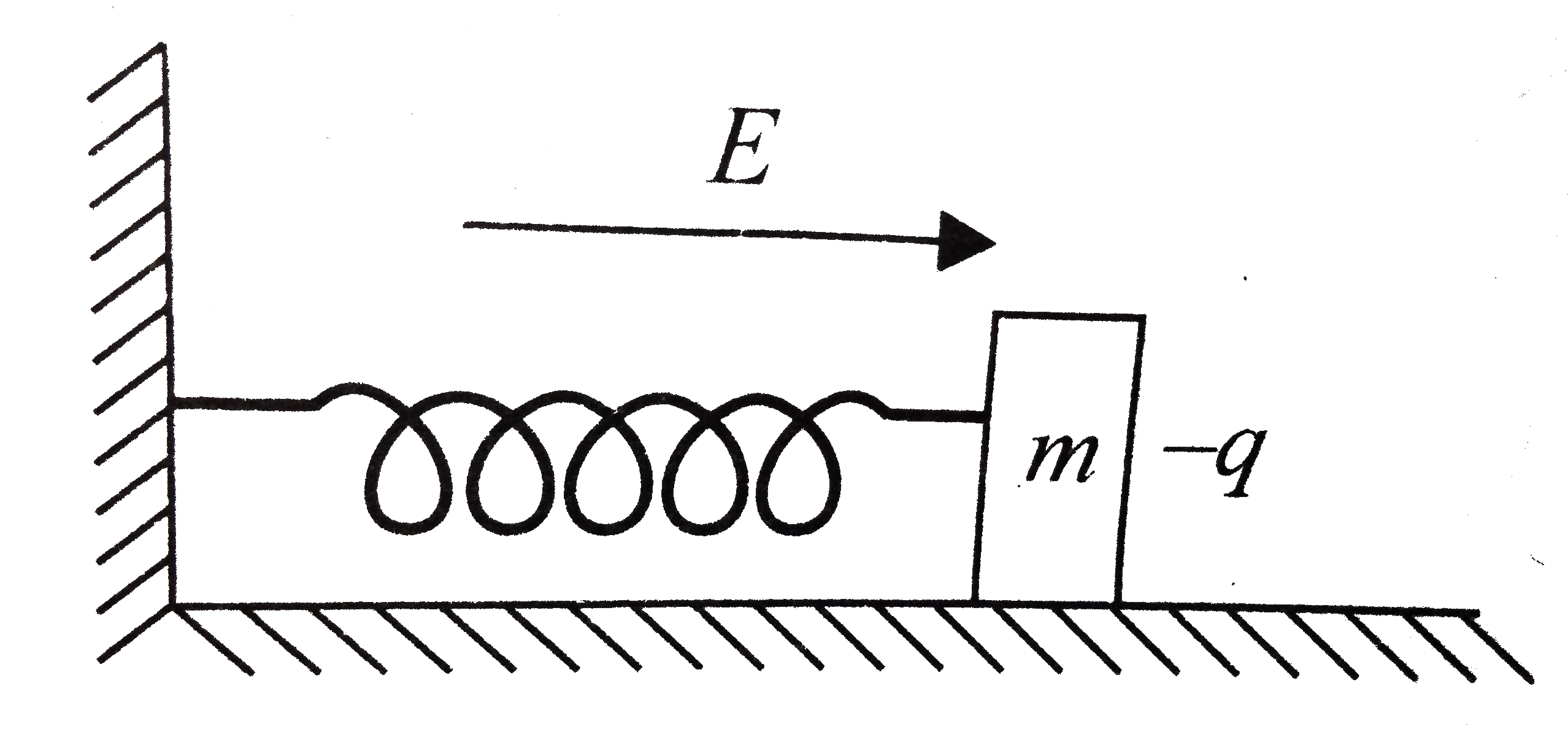
A block of mass m containing a net negative chage −q is placed on a froctionless horizontal tabe and is connected to a wall through an unstreached spring of spring constant k. If the horizontal electric field E parallel to spring is switched on , then the maximum compression of the spring is
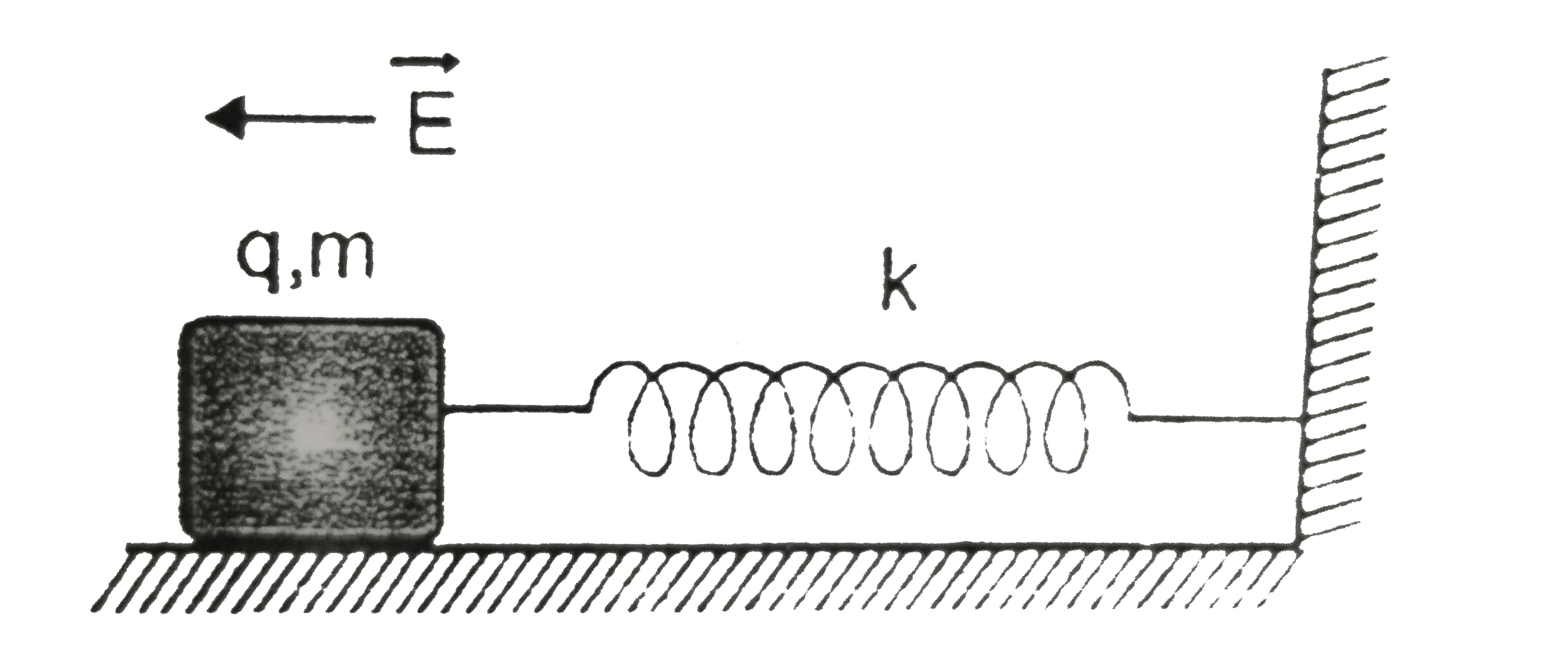
View SolutionA small cork block of mass m=1kg having charge q=−1C placed on a rough horizontal surface and is connected to a vertical wall through an unstretched non conducting light spring of spring consant k=9N/m as shown in the figure. If a horizontal constant electric field E=10N/C is switched on then the maximum compression in the spring is xm. Find the value of x. (Take g=10m/s2,μ=0.1)
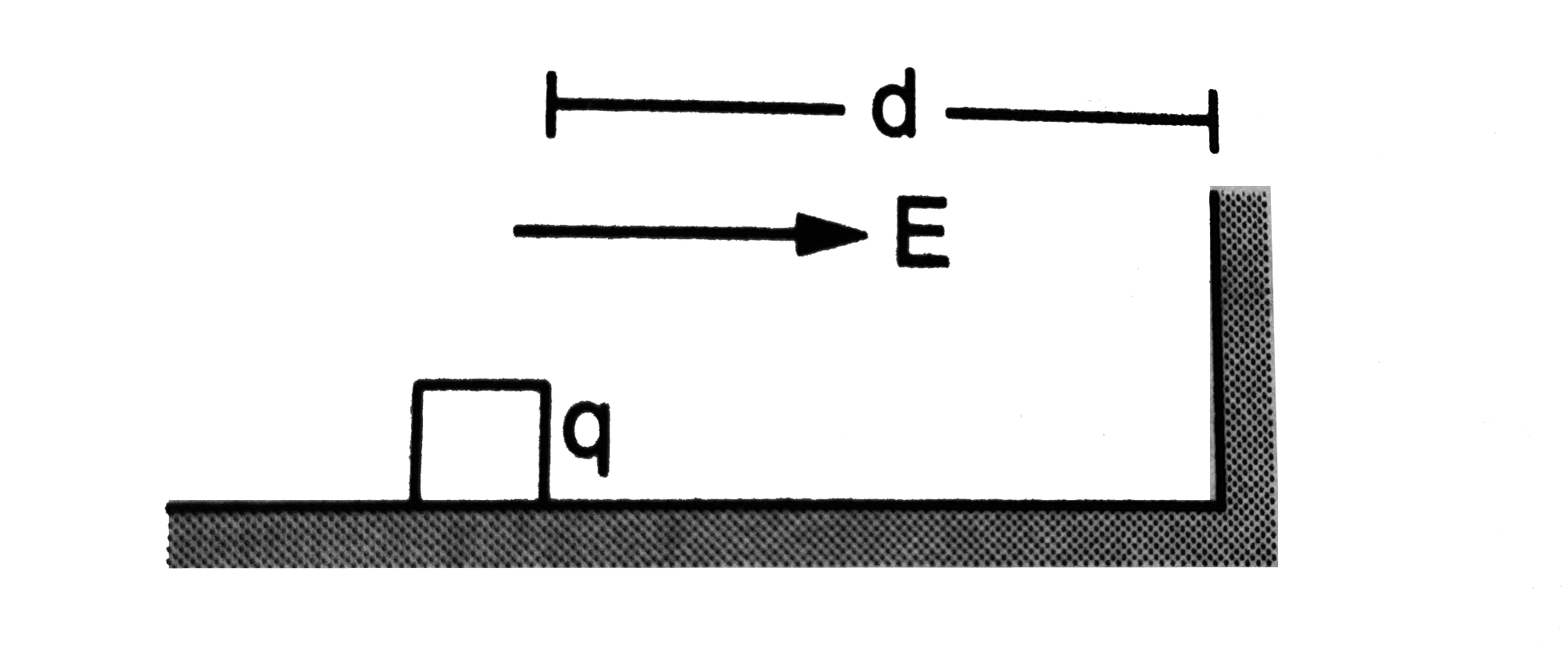
View SolutionA block of mass m containing a net positive charge q is placed on a smooth horizontal table which terminates in a vertical wall as shown in figure(29-E2). The distance of the block from the wall is d. A horizontal electric field E to towards right is switched on. Assuming elastic collisions find the time period of the resulting oscillatory motion. Is it a simple harmonic motion?
View SolutionA block of mass m is suspended by different springs of force constant shown in figure.

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
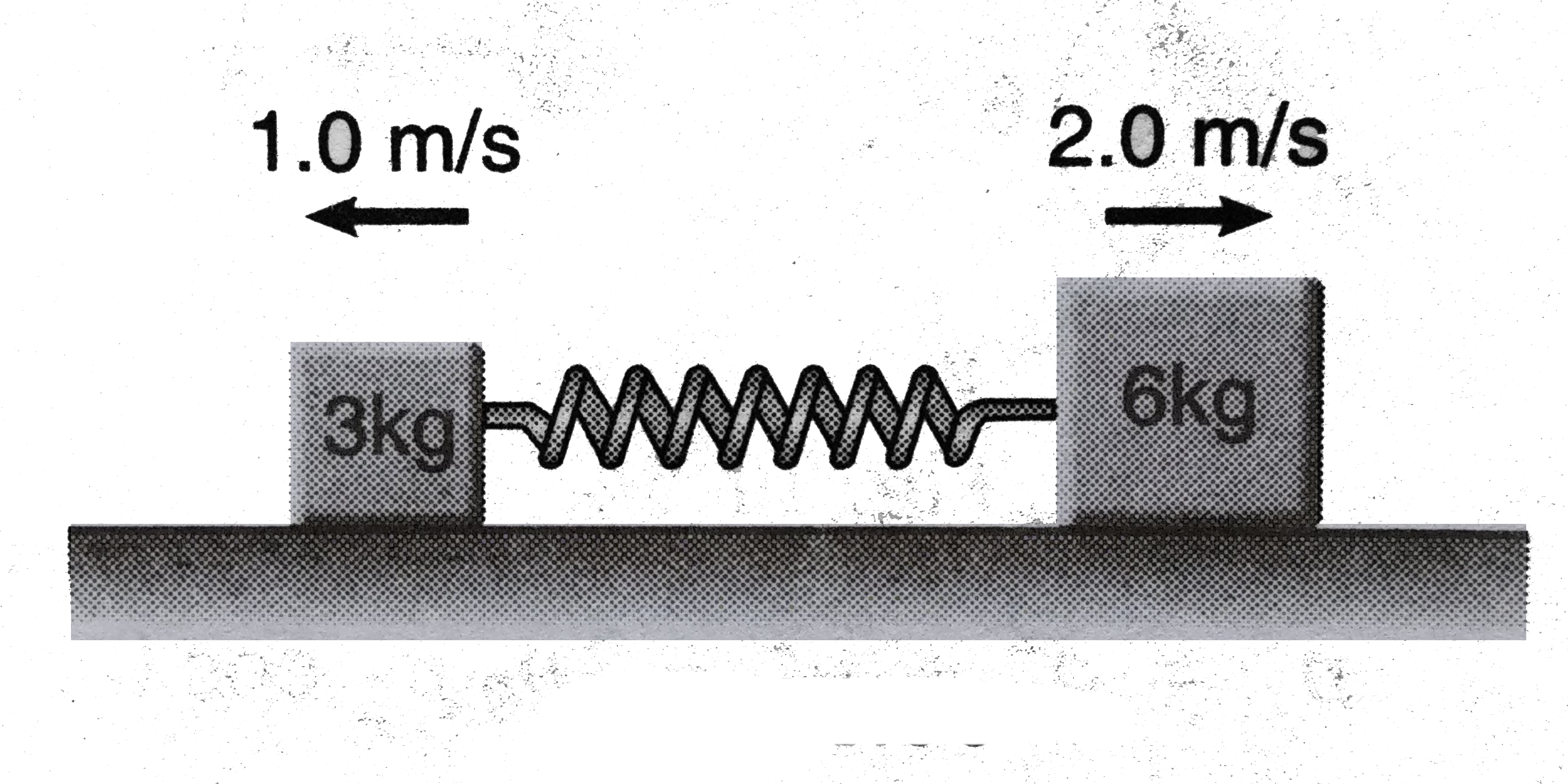
View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
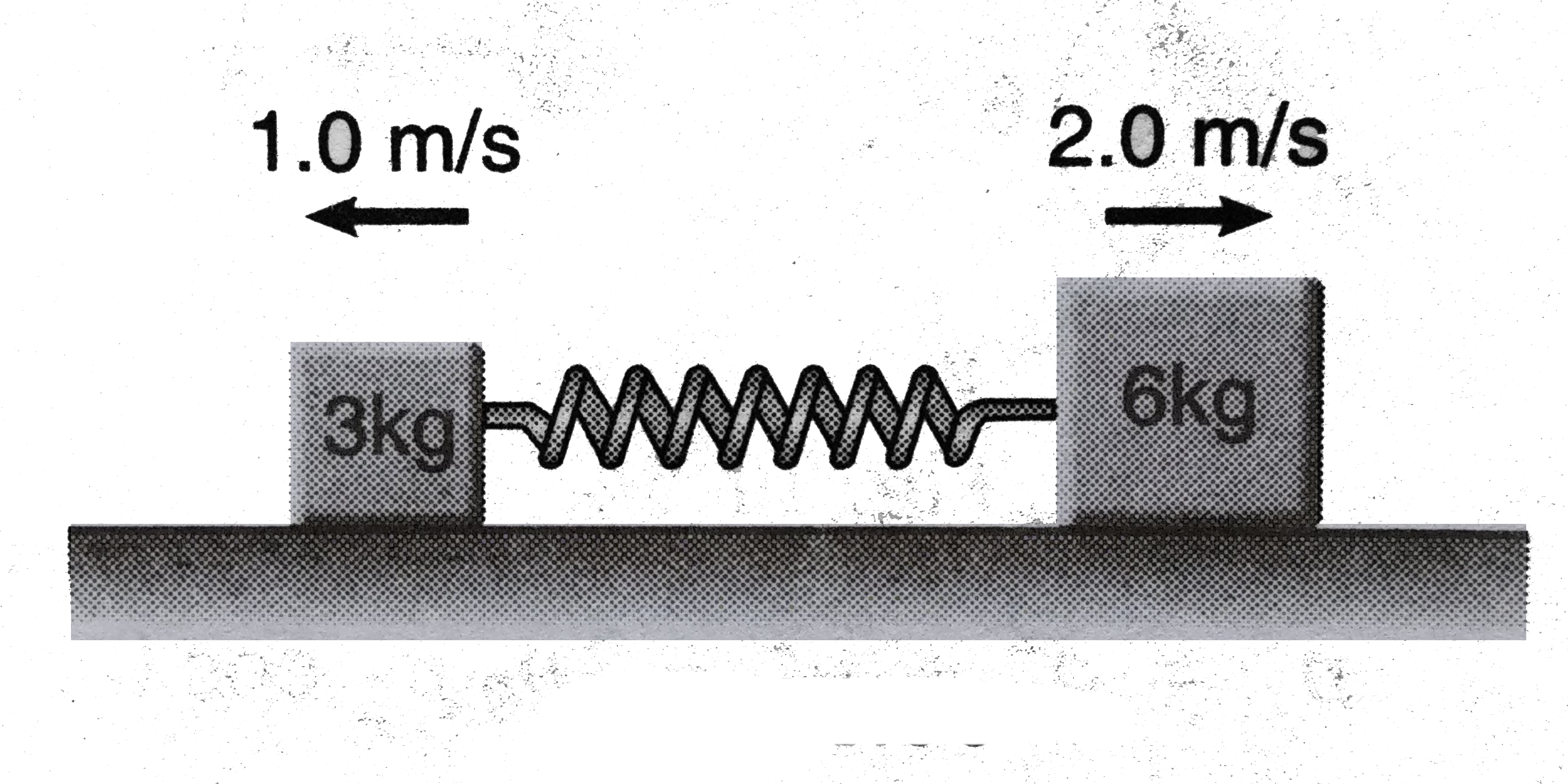
View SolutionA block of mass M=1 kg resting on a smooth horizontal surface is connected to a horizontal light spring of spring constant k=6N/m whose other end is fixed to a verticall wall. Another block of mass m=0.5 kg is placed over the block M. If the coefficient of friction between the two blocks μ=0.4, find the maximum kinetic energy (in J) that the system can have for simple hormonic oscillation under the action of the spring.
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA spring of spring constant 'K' is fixed at one end has a small block of mass m and charge q is attached at the other end. The block rests over a smooth horizontal surface. A uniform and constant magnetic field B exists normal to the plane of paper as shown in figure. An electric field →E=E0ˆi(E0 is a positive constant) is switched on at t=0 sec. The block moves on horizontal surface without ever lifting off the surface. Then the normal reaction acting on the block is :
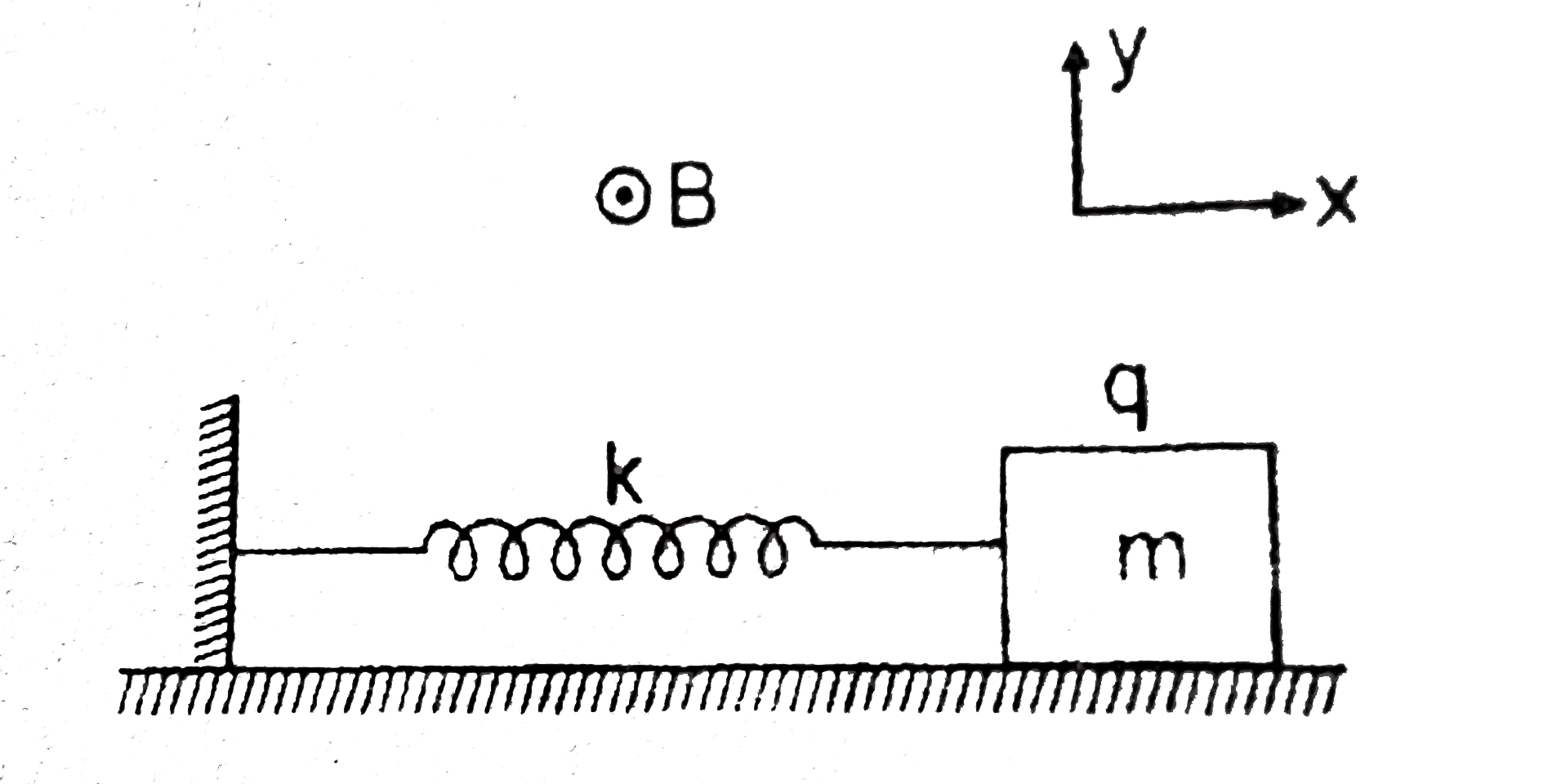
View Solution
