Find the equivalent capacitance between the point A and B in figure .

Text Solution
Let us connect a battery between the points A and B. The charge distribution is shown jin figure. Suppose the positive terminal of the battery supplies a charge +Q and the nagative terminal a charge -Q. The charge Q is divided between plates a can e. A charge <br>Q_1<br> goes to the plate a and the rest <br>Q-Q_1<br> goes to the plate e. The charge -Q supplied by the nagative terminal is divided between plates d and h. Using the symmetry of the figure, charge <br>-Q_1<br> goes to the plate h and <br>-(Q - Q_1)<br> to the plate d. This is because if you look into the circuit from A or from B, the circuit looks identical. The division of charge at A and at B should, therfore, be similar. The charges on the other plates may be written easily. The charge on the plate l is <br>2 Q_1 - Q<br> which ensures that the total charge on plates b,c and i remains zero as these three plates form an isolated system. we have <br>V_A V_B =(V_A - V_D) + (V_D - V_B)<br> = <br>(Q_1)/(C_1) + (Q- Q_1)/(C_2)<br> ... (i) Also, <br>V_A - V_B = (V_A - V_D) + (V_D - V_E) + (V_E - V_B)<br> = (Q_1)/(C_1) + (2Q_1 - Q)/(C_3) = (Q_1)/(C_1)<br>. ....(ii) We have to eliminate <br>Q_1<br> from these equations ot get the equivalent capacitance <br>Q/ (V_A- V_B)<br>. The first equation may be written as <br>V_A - V_B = Q_1 ((1)/(C_1) - (1)/(C_2)) + (Q)/(C_2)<br> or, <br>(C_1 C_2)/(C_2 - C_1) (V_A - V_B ) = Q_1 + (C_1)/(C_2 - C_1) Q<br>. The second equation may be written as <br> V_A - V_B = 2Q_1((1)/(C_1)+(1)/(C_3)) - (Q)/(C_3) or, (C_1 C_3)/(2(C1 + C_3) (V_A - V_B) = Q_1 - (C_1)/(2(C_1 + C_3) Q. ...(IV) Subtracting (iv) from (iii) <br>(V_A - V_B)[(C_1 C_2)/(C_2 - C_1) - (C_1 C_3) /(2(C_1 + C_3))]<br> <br> = [(C_1)/(C_2 -C_1) +(C_1)/(2(C_1 + C_3)] Q<br> or <br>(V_A - V_B) [2 C_1 C_2(C_1 + C_3) + (C_2 - C_1)]<br> <br>=C_1[2(C_1 + C_3) + (C_2 - C_1)] Q<br> or, <br> C = (Q)/(V_A - V_B) = (2 C_1 C_2 + C_2 C_3 + C_3 C_1)/( C_1 + C_2 + 2C_3)<br>.
|
Topper's Solved these Questions
- CAPACITORSBook:HC VERMA ENGLISHChapter:CAPACITORSExercise:Objective 1
Explore 12 Videos
- CAPACITORSBook:HC VERMA ENGLISHChapter:CAPACITORSExercise:OBJECTIVE 2
Explore 6 Videos
- CAPACITORSBook:HC VERMA ENGLISHChapter:CAPACITORSExercise:short answer
Explore 7 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBook:HC VERMA ENGLISHChapter:BOHR'S MODEL AND PHYSICS OF THE ATOMExercise:Short Answer
Explore 10 Videos
- DISPERSION AND SPECTRABook:HC VERMA ENGLISHChapter:DISPERSION AND SPECTRAExercise:Question for short Answer
Explore 6 Videos
Similar Questions
The equivalent capacitance between the points A and B is
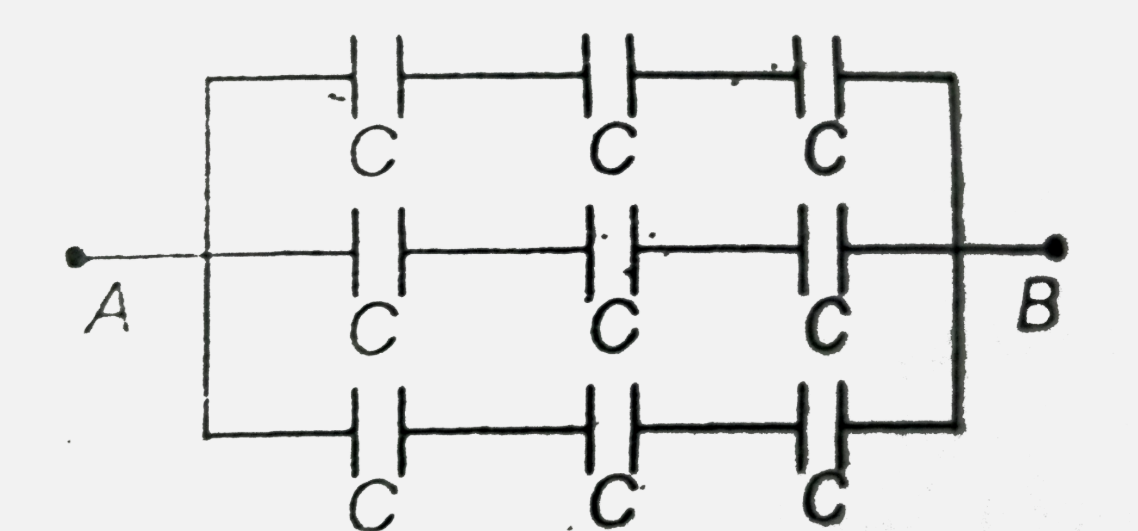
View SolutionThe equivalent capacitance between the points A and B is

View SolutionThe equivalent capacitance between the points A and B is

View SolutionFind the equivalent capacitance between point A and B .
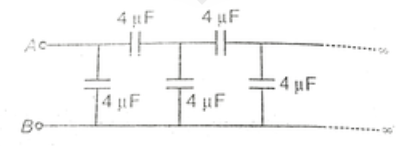
View SolutionFind the equivalent capacitance between A&B
View Solution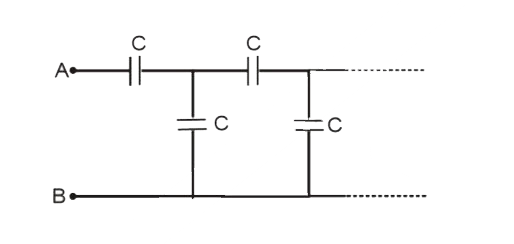 Find equivalent capacitance between point A and B
Find equivalent capacitance between point A and B
View Solution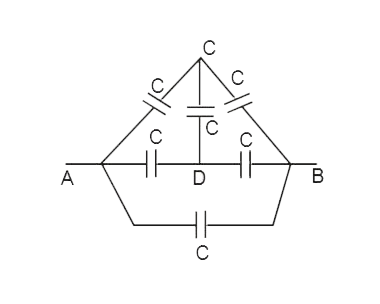 Find equivalent capacitance between point A and B
Find equivalent capacitance between point A and B
View Solution Find equivalent capacitance between point A and B
Find equivalent capacitance between point A and B
View SolutionFind equivalent capacitance between points A and B

View SolutionFind equivalent capacitance between points A and B

View Solution
