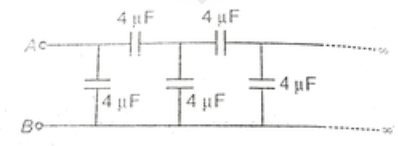
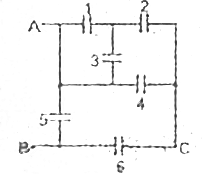
Find the equivalent capacitance of the point A and B .
Let the equivalent capacitance be C, since it is an infinite series , So there will be negligible change if the arrangement is doen as in (fig.)
From figure Ceq=1
⇒(2+C)C=3C+2
⇒2C+C2=3C+2C
⇒C2−C−2=0
⇒(C−2)(C+1)=0
⇒C=−1(impossib≤),
So, C=2MF.
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer
7 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 2
6 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
Knowledge Check
Six plates each of area A arranged as shown· in figure. The separation between adjoining plates is d. Find the equivalent capacitance between points A and B :
 Aε0AdB7ε0AdC6ε0AdD5ε0Ad
Aε0AdB7ε0AdC6ε0AdD5ε0Ad
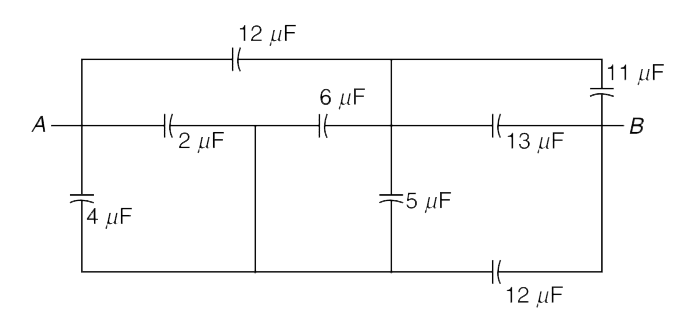
Find the equivalent capacitance between the point A and B in figure .

View SolutionFive capacitors are connected as shown in figure. Find the equivalent capacitance between points A and B.

View Solution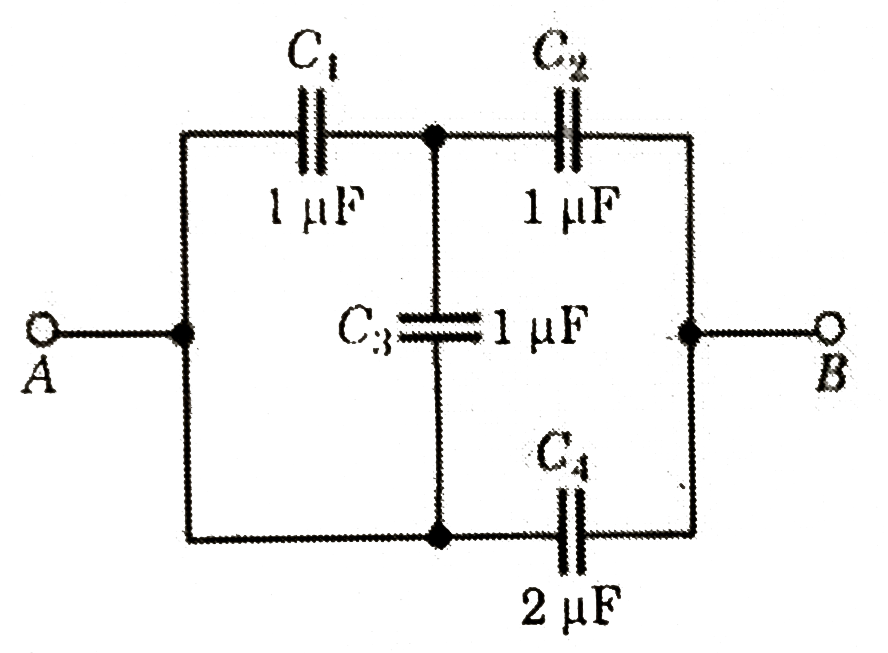
Find the equivalent capacitance between points A and B for the network shown in figure.
View SolutionFind the equivalent capacitance between points A and B. Capacitance of each capacitor is 2μF.
View SolutionFigure shows two capacitors of capacitance 2μF and 4μF and a cell of 90 V. The switch 'k' is such that when it is in position 1, the circuit ABCD is closed and when it is in position 2, the circuit BCEF is closed.the resistance of both the circuits is negligible os that the capacitor gets fully charged instantly. Initially the switch is in position1. then it is turned in position 2 and then in position 1. Now two cycles are completed. Find the charge (inμC) after two cycles.
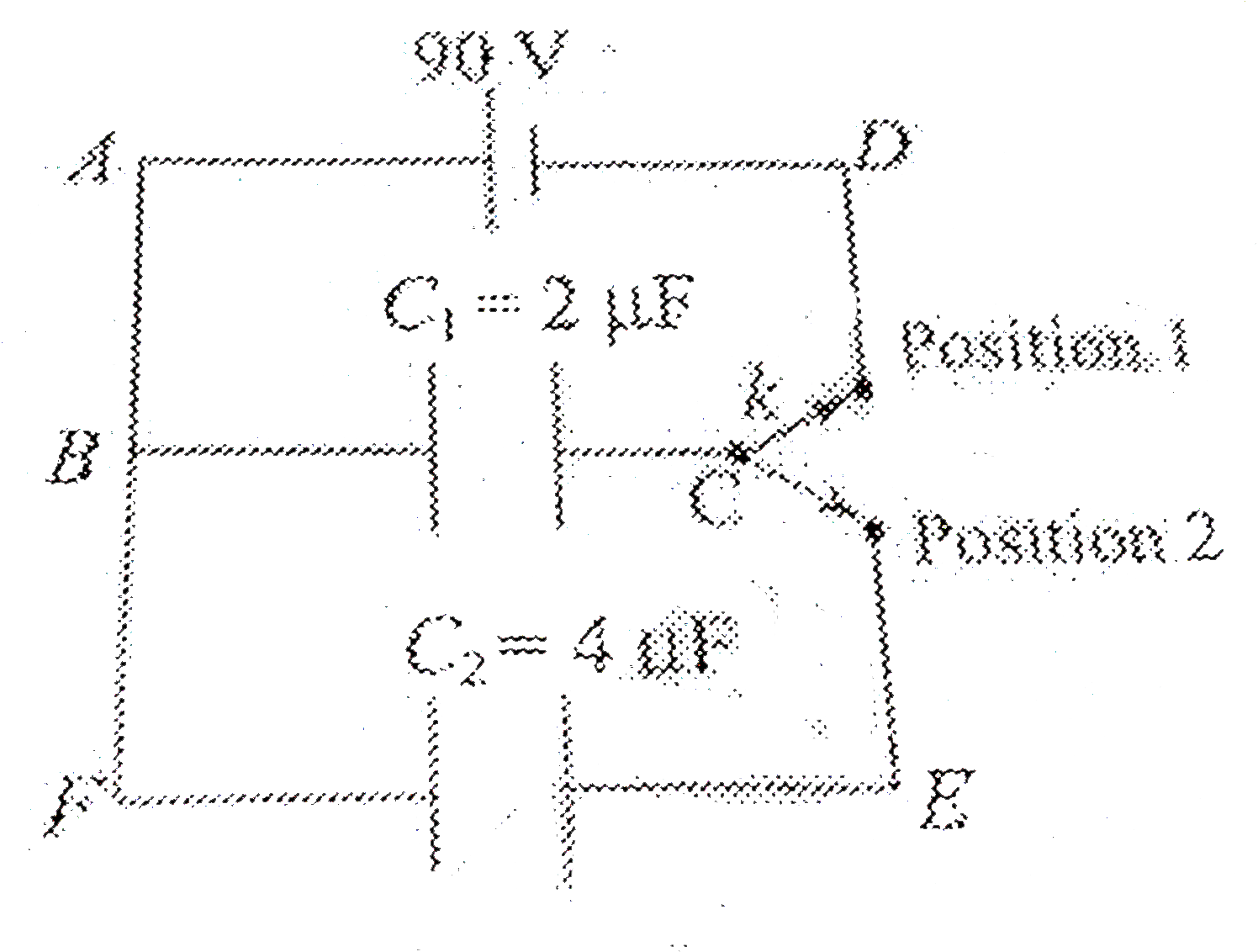
View SolutionFind the equivalent capacitance between points A and B. Capacitance of each capacitor is 2μF.

View Solution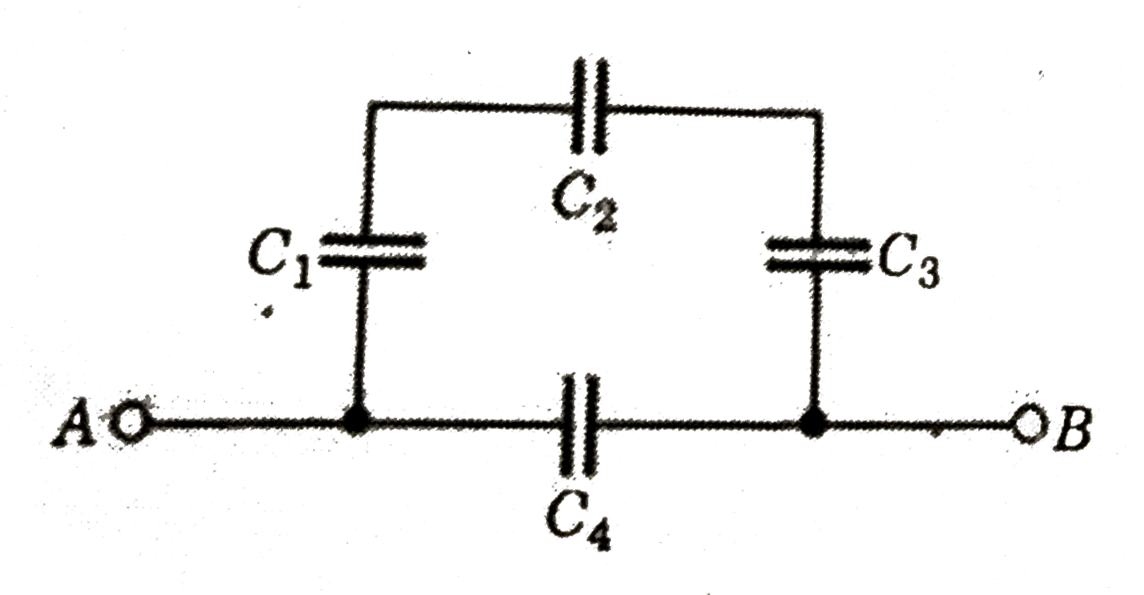
In the network shown in figure. C1=C2=C3=C4=10μF. Find th equivalent capacitance between the points A and B, what will be the charge on each capacitor?
View Solution