An infinite ladder is constructed by connecting several sections of2μF,4μF capacitor combinations as shown in figure . It is terminated by a capacitor of capacitance C . What value should be chosen for C, such that the equivalent capacitance of the number of sections in between ?
To solve the problem of finding the value of capacitance C that should be chosen to terminate the infinite ladder of capacitors, we can follow these steps:
Step 1: Understand the Configuration
The infinite ladder consists of sections of capacitors 2μF and 4μF. The last section is terminated by a capacitor C.
Step 2: Identify the Equivalent Capacitance
Let the equivalent capacitance of the entire ladder be C. The first section of the ladder consists of a 4μF capacitor in series with the capacitor C. The formula for capacitors in series is:
C1=C⋅4C+4
Step 3: Redraw the Circuit
Now, we can redraw the circuit where the 2μF capacitor is in parallel with C1:
C=C1+2μF
Substituting C1:
C=C⋅4C+4+2
Step 4: Solve for C
Now, we can solve the equation:
1. Multiply both sides by C+4 to eliminate the fraction:
C(C+4)=4C+8(C+4)
2. Expand both sides:
C2+4C=4C+8C+32
3. Simplify the equation:
C2+4C−12C−32=0
C2−8C−32=0
Step 5: Apply the Quadratic Formula
Now we can apply the quadratic formula C=−b±√b2−4ac2a:
Here, a=1,b=−8,c=−32:
C=8±√(−8)2−4⋅1⋅(−32)2⋅1
C=8±√64+1282
C=8±√1922
C=8±8√32
C=4±4√3
Step 6: Select the Positive Value
Since capacitance cannot be negative, we take the positive value:
C=4+4√3μF
Final Answer
Thus, the value of C that should be chosen is:
C=4+4√3μF
---
The infinite ladder consists of sections of capacitors 2μF and 4μF. The last section is terminated by a capacitor C.
Let the equivalent capacitance of the entire ladder be C. The first section of the ladder consists of a 4μF capacitor in series with the capacitor C. The formula for capacitors in series is:
Now, we can redraw the circuit where the 2μF capacitor is in parallel with C1:
Now, we can solve the equation:
C2−8C−32=0
Now we can apply the quadratic formula C=−b±√b2−4ac2a:
C=8±√64+1282
C=8±√1922
C=8±8√32
C=4±4√3
Since capacitance cannot be negative, we take the positive value:
Thus, the value of C that should be chosen is:
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer
7 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 2
6 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
An infinite ladder is constructed by connecting several sections of 2 μF,4μF capacitor combination as shown in figure . It is terminated by a capacitor of capacitance C. What value should be chosen for C such that the equivalent capacitance of the ladder between points A and B becomes independent of the number of sections in between
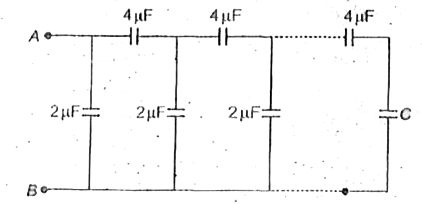
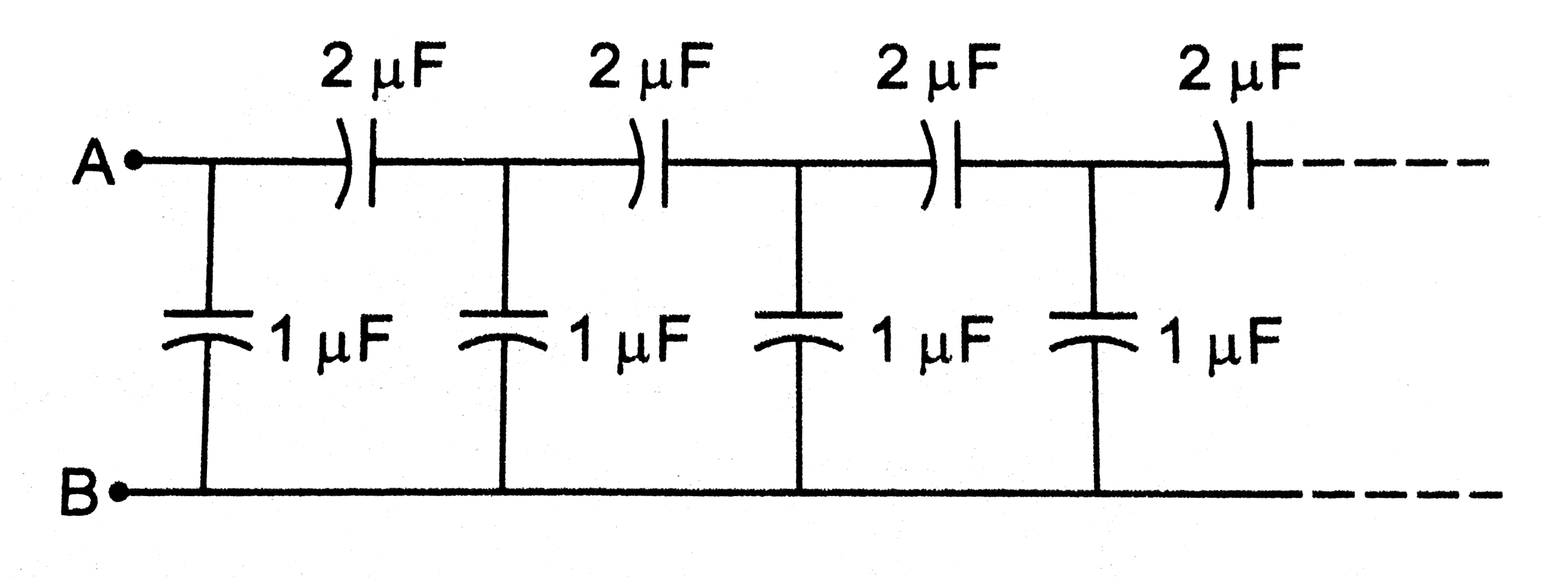
View SolutionA finit ladder is constructed by connecting several sections of2μF,1μF capacitor combinations as shown in figure . It is terminated by a capacitor of capacitance C . What value should be chosen for C, such that the equivalent capacitance of ladder between the points A and B becomes independent of the number of sections in between ?
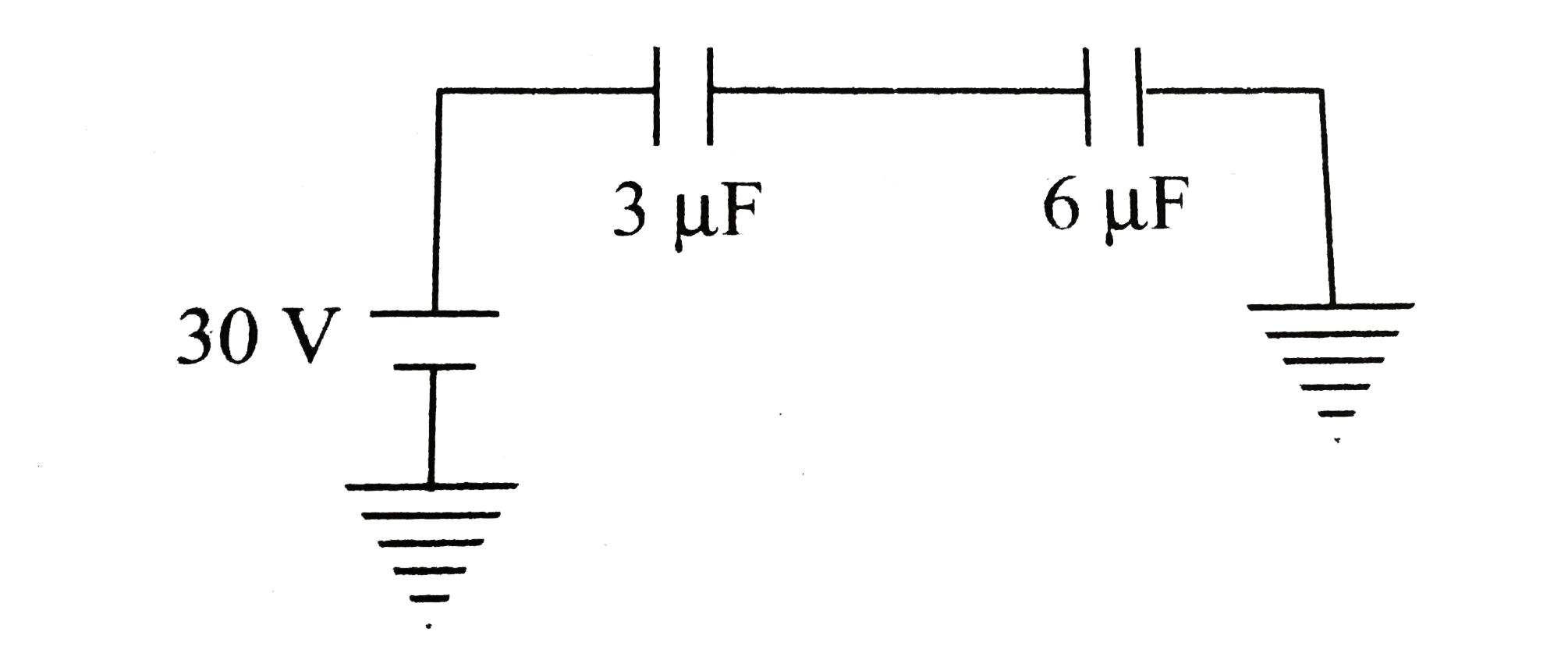
View SolutionIn the circuit shown in figure, the charge stored on a capacitor of capacitance 3μF is
View SolutionSix equal capacitors each of capacitance 10μF are connect as shown in the figure. Then the equivalent capacitance between A and B is
View SolutionSome capacitors each of capacitance 30μF are connected as shown in. Calculate the equivalent capacitance between terminals A and B
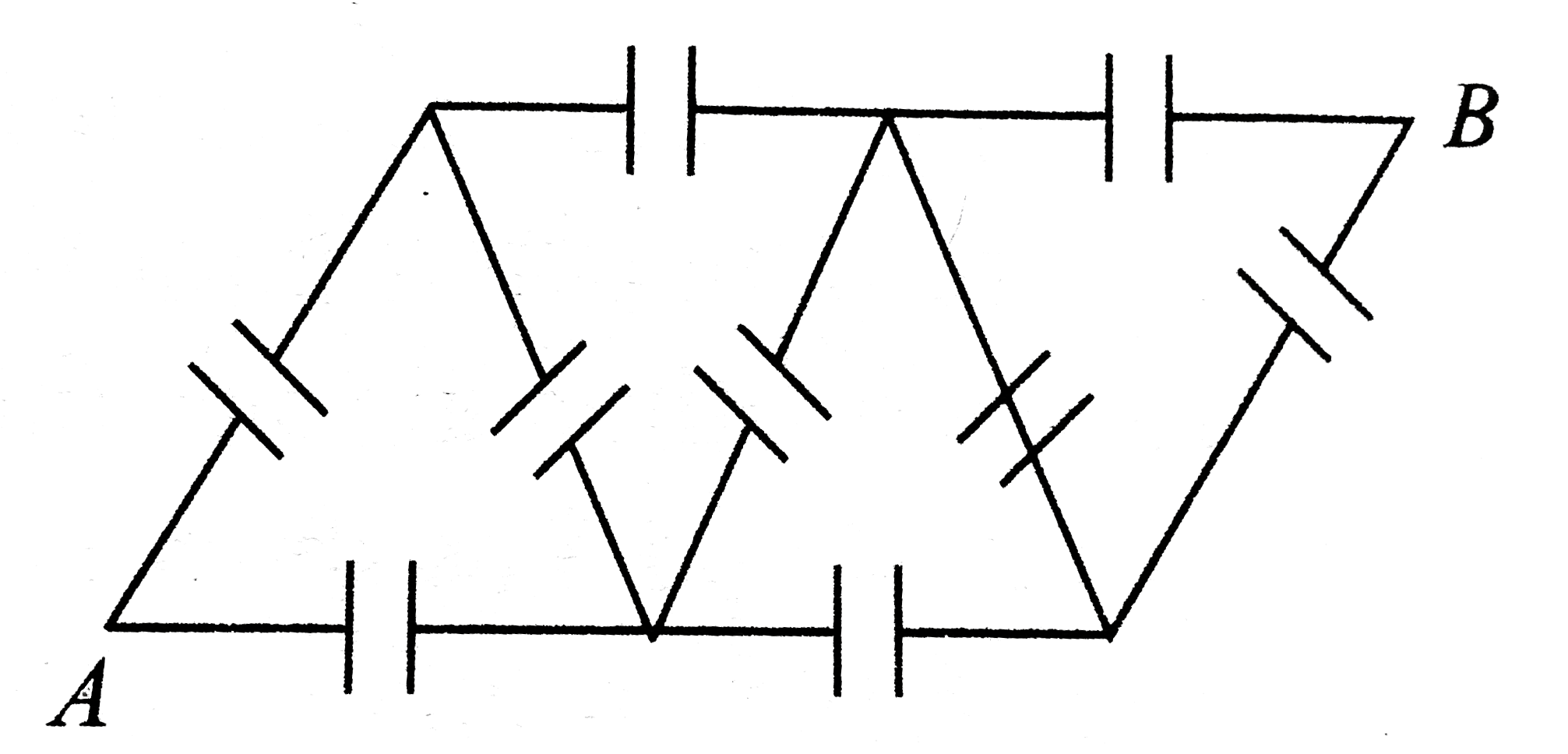 .
.
View SolutionSix equal capacitors each of capacitance C are connected as shown in the figure. The equivalent capacitance between points A and B is
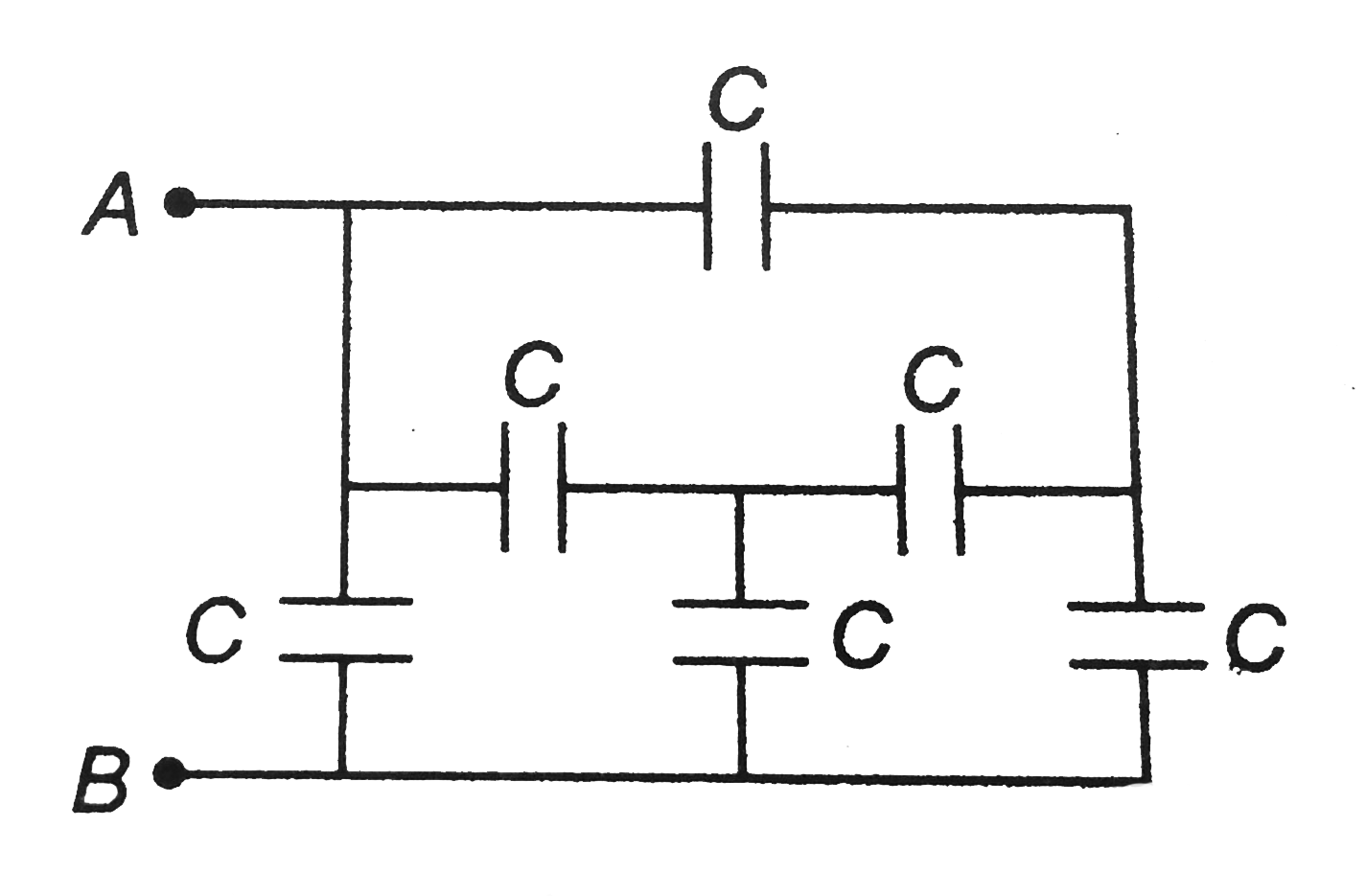
View SolutionAn infinite number of identical capacitors each of capacitance 1mF are connected as shown in the figure. Then the equivalent capacitance between A and B is.
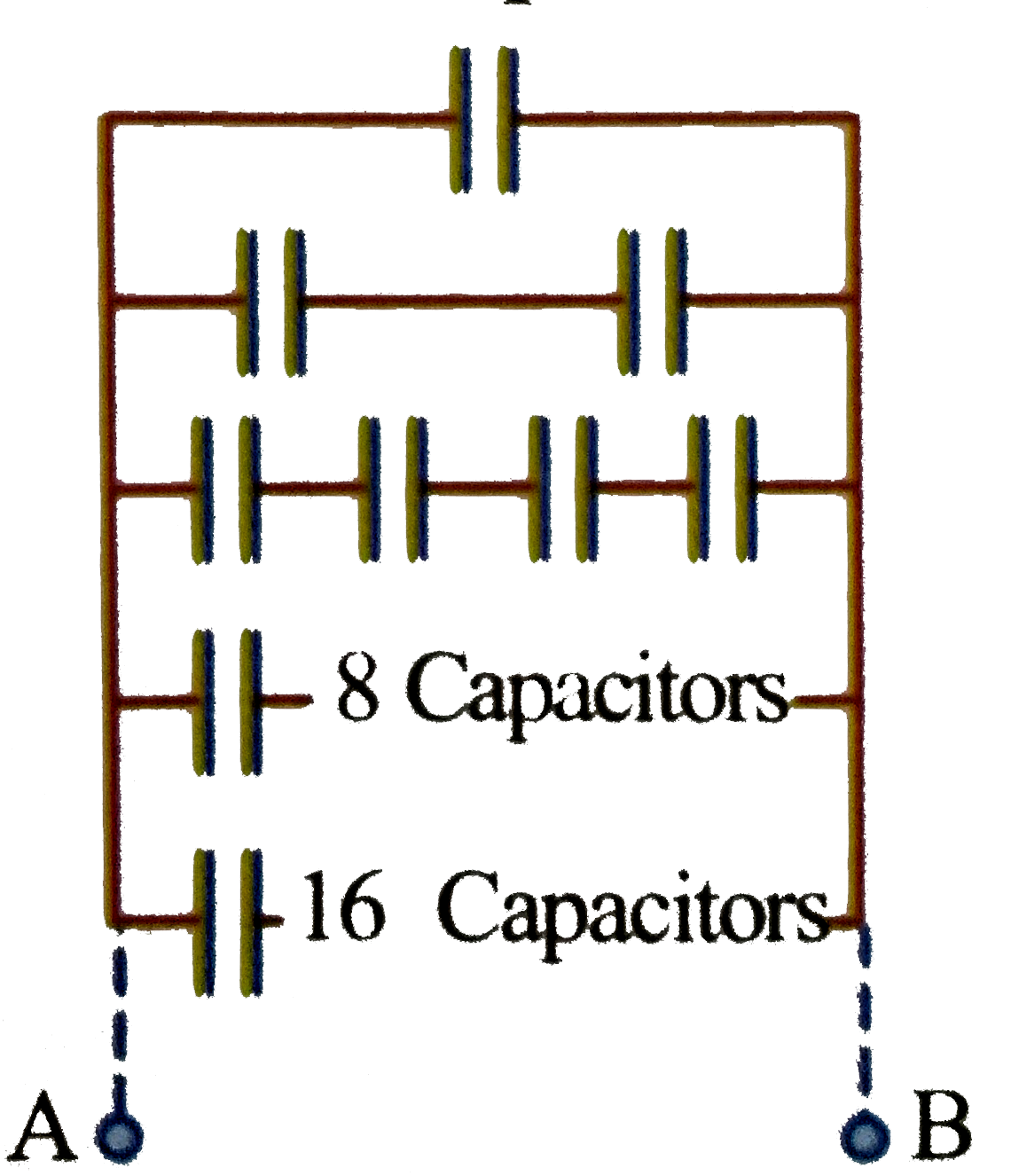 .
.
View SolutionAn infinite number of identical capacitors each of capacitance 1mF are connected as shown in the figure. Then the equivalent capacitance between A and B is.
 .
.
View SolutionThree equal capacitors, each with capacitance C are connected as shown in figure. Then the equivalent capacitance between A and B is
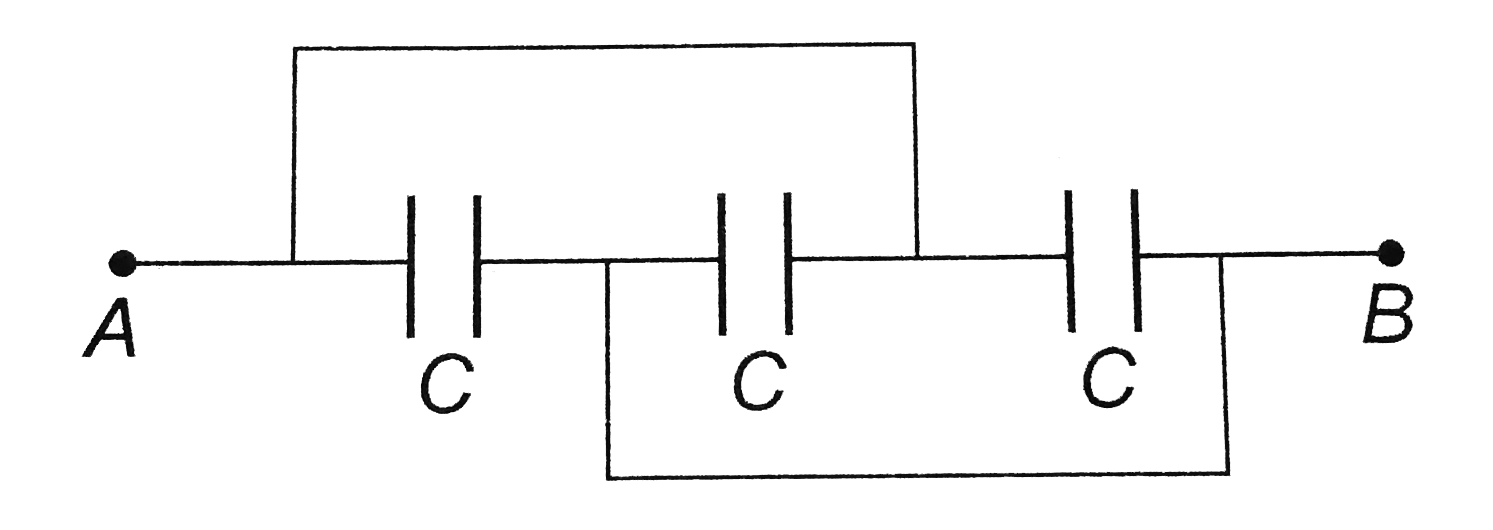
View SolutionSix identical capacitors each of capacitance 2μF are connected as shown below. The equivalent capacitance between the points A and B is
View Solution

