The switch S shown in figure is kept closed for a long time and is then opened at t=0.Find the current in the middle 10(Ω)resistor at t=1.0ms.
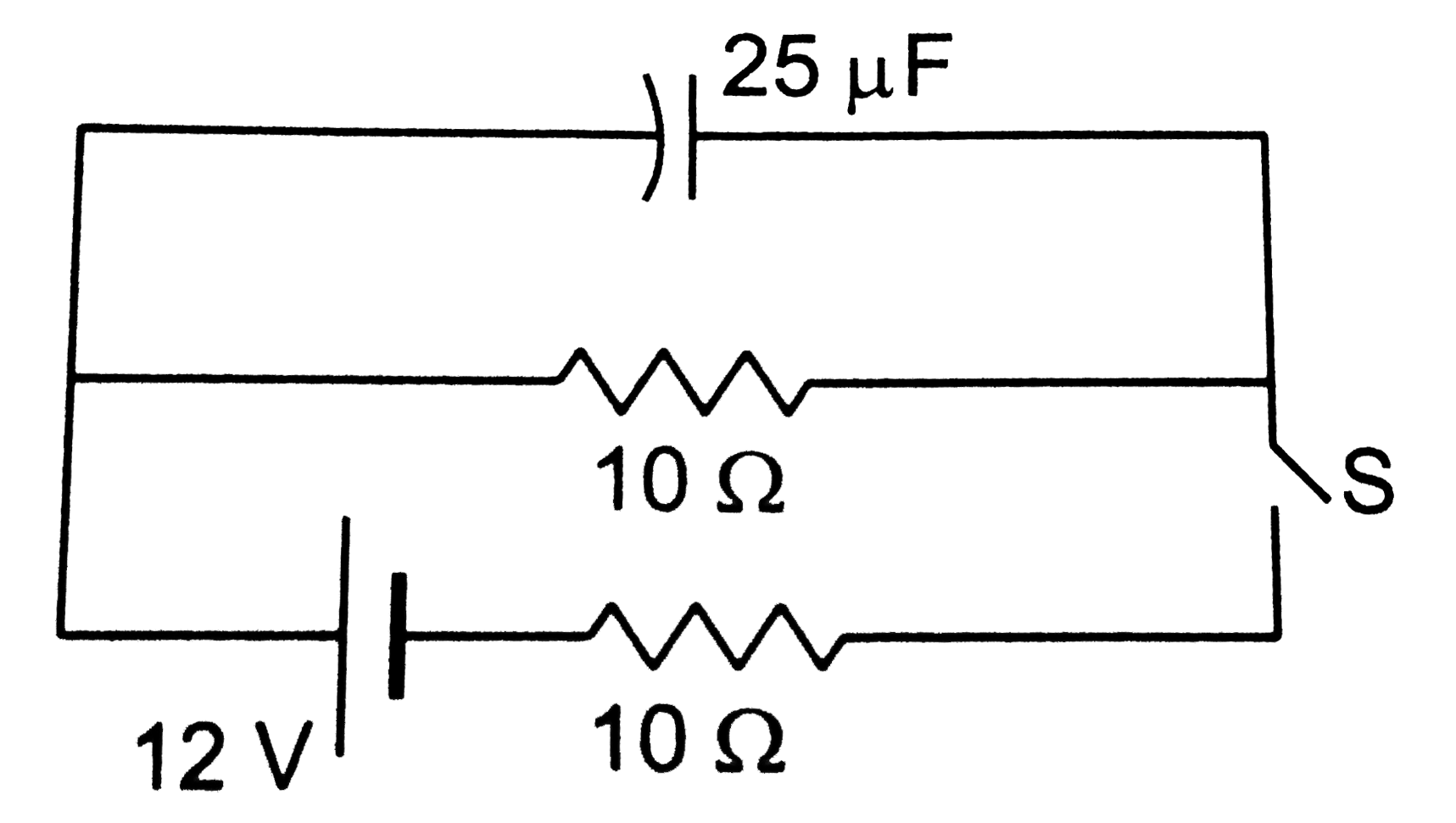
In steady state condition,
Potential difference across the capacitor
=25μF
Potentiald⇔erenceacrossthe10Ω<br>resistance<br> = 12/5 xx 10 = 24V <br> Q = (Q_0) e^(t/RC) = V xx C (e ^-t/RC))<br> = 24 xx 25 xx (10^-6)e^(-4) <br> = 24 xx 25 xx (10^-6) xx 0.0183 <br> 10.9 xx (10^-6) C <br>Char≥bythe∩aci→raftertimet'<br>Current∈the10Ωresis→r<br> = (10.9 xx (10^-6)C/1 xx (10^-3) sec) = 11 mA.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer
17 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 2
9 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions

System is shown in the figure. Velocity of sphere A is 9 ms. Find the speed of sphere B.
View SolutionFind the current through the 10(Ω)resistor shown in figure.

View SolutionIf the switch is closed for long time and then open at t=0, the P.D across indicator at t=0 is

View SolutionIn Fig. switch S is closed for a long time. At t=0, if it is opened, then

View SolutionIn Fig. switch S is closed for a long time. At t=0, if it is opened, then

View SolutionThe switches in figure and are closed at =0 and reopended after a long time at t=t0.
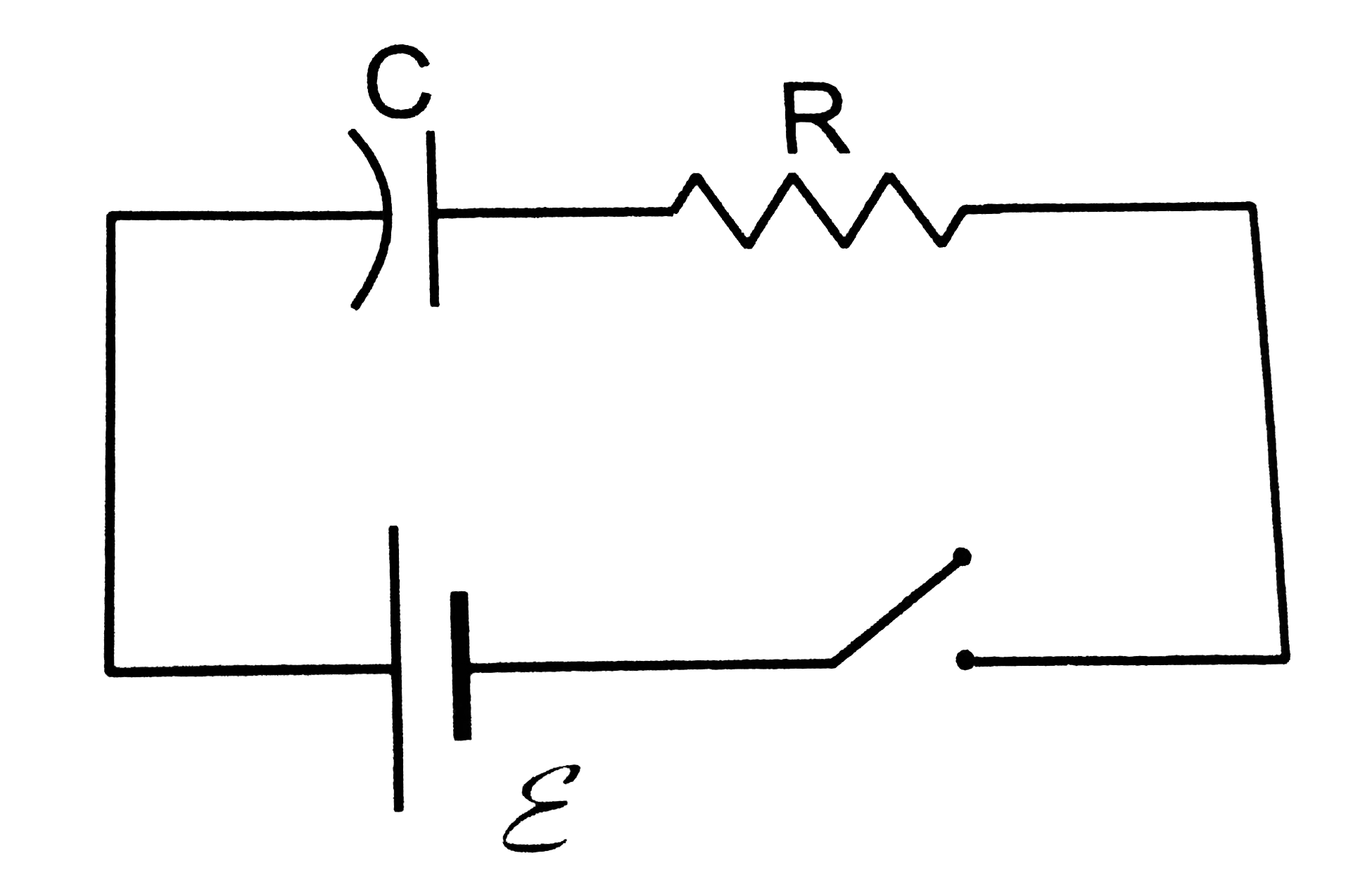
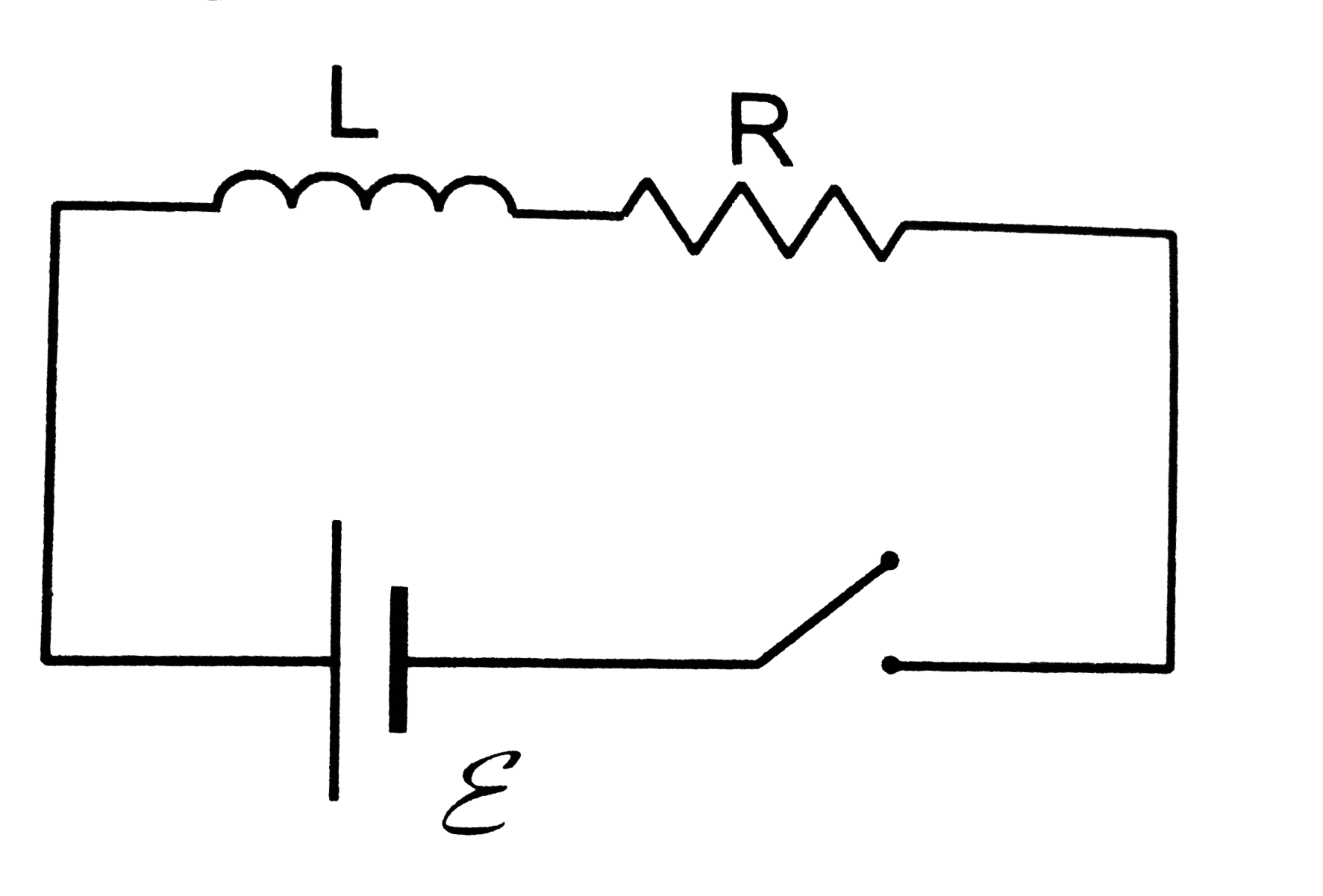
View SolutionThe switches in figure and are closed at =0 and reopended after al long time at t=t0.


View SolutionThe switch shown in figure is closed at t=0 find the charge throuh battery till time t=LR
_2019_CBT8_E01_016_Q01.png)
View SolutionThe switch shown in figure is closed at t=0 find the charge throuh battery till time t=LR
_2019_CBT8_E01_016_Q01.png)
View SolutionSwitch S shown in Fig. is closed for t<0 and is opened at t=0. When currents through L1 and L2 are equal, their common value is

View Solution
