Is it possible for a current loop to stay without rotating in a uniform magnetic field? If yes, what should be the orientation of the loop?
To determine if a current loop can stay without rotating in a uniform magnetic field, we need to analyze the conditions under which the torque acting on the loop is zero.
1. Understanding Torque on a Current Loop:
- The torque (τ) experienced by a current loop in a magnetic field is given by the formula:
τ=B⋅I⋅A⋅sin(θ)
where:
- B = magnetic field strength
- I = current flowing through the loop
- A = area of the loop
- θ = angle between the magnetic field and the normal to the plane of the loop.
2. Condition for Zero Torque:
- For the loop to remain stationary (without rotating), the torque must be zero:
τ=0
- From the torque equation, we see that this occurs when:
sin(θ)=0
- This condition is satisfied when:
θ=0∘orθ=180∘
3. Orientation of the Loop:
- When θ=0∘, the plane of the loop is parallel to the magnetic field lines.
- When θ=180∘, the plane of the loop is also parallel to the magnetic field lines but in the opposite direction.
- In both cases, the normal to the loop is aligned with the magnetic field, which means there is no torque acting on the loop.
4. Conclusion:
- Yes, it is possible for a current loop to stay without rotating in a uniform magnetic field.
- The orientation of the loop should be such that the plane of the loop is either parallel to the magnetic field (θ=0∘) or anti-parallel to the magnetic field (θ=180∘).
- The torque (τ) experienced by a current loop in a magnetic field is given by the formula:
τ=B⋅I⋅A⋅sin(θ)
where:
- B = magnetic field strength
- I = current flowing through the loop
- A = area of the loop
- θ = angle between the magnetic field and the normal to the plane of the loop.
- For the loop to remain stationary (without rotating), the torque must be zero:
τ=0
- From the torque equation, we see that this occurs when:
sin(θ)=0
- This condition is satisfied when:
θ=0∘orθ=180∘
- When θ=0∘, the plane of the loop is parallel to the magnetic field lines.
- When θ=180∘, the plane of the loop is also parallel to the magnetic field lines but in the opposite direction.
- In both cases, the normal to the loop is aligned with the magnetic field, which means there is no torque acting on the loop.
- Yes, it is possible for a current loop to stay without rotating in a uniform magnetic field.
- The orientation of the loop should be such that the plane of the loop is either parallel to the magnetic field (θ=0∘) or anti-parallel to the magnetic field (θ=180∘).
Topper's Solved these Questions
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - Exercises
60 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
Similar Questions
A current loop of arbitrary shape lies in a uniform magnetic field B. show that the net magnetic force acting on the loop is zero.
View SolutionA current carrying loop in a uniform magnetic field will experience
View SolutionA current loop in a magnetic field
View SolutionTorque acting on a current loop in a uniform magnetic field is equal to
View SolutionA circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
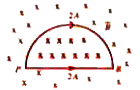
View SolutionA circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop

View SolutionStatement 1: A rectangular current loop is in an arbitray oreintation in an external uniform magnetic field. No work is required to rotate the loop abour an axis perpendicular to its plane.
Statement 2: All positions represents the same level of energy.
View SolutionA current carrying circular loop is located in a uniform external magnetic field. If the loop if free to turn, what is its orientation of stable equilibrium? Show that in this orientation, the flux of the total field (external field + field produced by the loop) is maximum.
View SolutionWill there be any tension in a current carrying loop placed in uniform magnetic field ? If yes, will it be equal to BiR ?
View Solution
