Will there be any tension in a current carrying loop placed in uniform magnetic field ? If yes, will it be equal to BiR ?
The correct Answer is:Yes, yes
To determine whether there is any tension in a current-carrying loop placed in a uniform magnetic field and if that tension is equal to BiR, we can follow these steps:
1. Understanding the Setup:
- Consider a circular loop of radius R carrying a current I.
- The loop is placed in a uniform magnetic field B directed inward.
2. Analyzing a Small Section of the Loop:
- Focus on a small section of the loop that subtends an angle θ at the center of the loop.
- The length of this small section can be expressed as dL=R⋅dθ.
3. Calculating the Magnetic Force on the Section:
- The magnetic force dF on this small section due to the magnetic field can be calculated using the formula:
dF=I⋅dL⋅B⋅sin(θ)
- Since the magnetic field is perpendicular to the current in this case, we can simplify this to:
dF=I⋅dL⋅B
4. Direction of the Force:
- Using the right-hand rule, the direction of the force dF will be upward, while the tension T in the loop acts downward.
5. Balancing Forces:
- The upward force due to the magnetic field must be balanced by the downward tension in the loop.
- For a small angle θ, we can consider the vertical component of the tension acting on both sides of the small section:
2T⋅sin(θ2)=dF
6. Using Small Angle Approximation:
- For small angles, sin(θ2)≈θ2.
- Therefore, the equation becomes:
2T⋅θ2=I⋅(R⋅dθ)⋅B
- Simplifying gives:
T⋅θ=I⋅R⋅B⋅dθ
7. Final Expression for Tension:
- Rearranging the equation, we find:
T=I⋅R⋅B
8. Conclusion:
- Yes, there is tension in the current-carrying loop placed in a uniform magnetic field, and it is indeed equal to T=BIR.
- Consider a circular loop of radius R carrying a current I.
- The loop is placed in a uniform magnetic field B directed inward.
- Focus on a small section of the loop that subtends an angle θ at the center of the loop.
- The length of this small section can be expressed as dL=R⋅dθ.
- The magnetic force dF on this small section due to the magnetic field can be calculated using the formula:
dF=I⋅dL⋅B⋅sin(θ)
- Since the magnetic field is perpendicular to the current in this case, we can simplify this to:
dF=I⋅dL⋅B
- Using the right-hand rule, the direction of the force dF will be upward, while the tension T in the loop acts downward.
- The upward force due to the magnetic field must be balanced by the downward tension in the loop.
- For a small angle θ, we can consider the vertical component of the tension acting on both sides of the small section:
2T⋅sin(θ2)=dF
- For small angles, sin(θ2)≈θ2.
- Therefore, the equation becomes:
2T⋅θ2=I⋅(R⋅dθ)⋅B
- Simplifying gives:
T⋅θ=I⋅R⋅B⋅dθ
- Rearranging the equation, we find:
T=I⋅R⋅B
- Yes, there is tension in the current-carrying loop placed in a uniform magnetic field, and it is indeed equal to T=BIR.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment (Section A) Objective Type Questions (One option is correct)
55 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment (Section B) Objective Type Questions (One option is correct)
35 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Illustration
14 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Knowledge Check
A current carrying loop is placed in a uniform magnetic field. The torque acting on it does not depend upon
Aarea of loopBvalue of currentCmagnetic fieldDNone of these
A coil carrying electric current is placed in uniform magnetic field
View SolutionA current loop placed in a magnetic field behaves like a
View SolutionTorque acting on a current loop in a uniform magnetic field is equal to
View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View SolutionAssertion : A current carrying loop is placed in uniform magnetic field as shown in figure. Torque in the loop in this case is zero.
Reason : Magnetic moment vector of the loop is perpendicular to paper inwards.
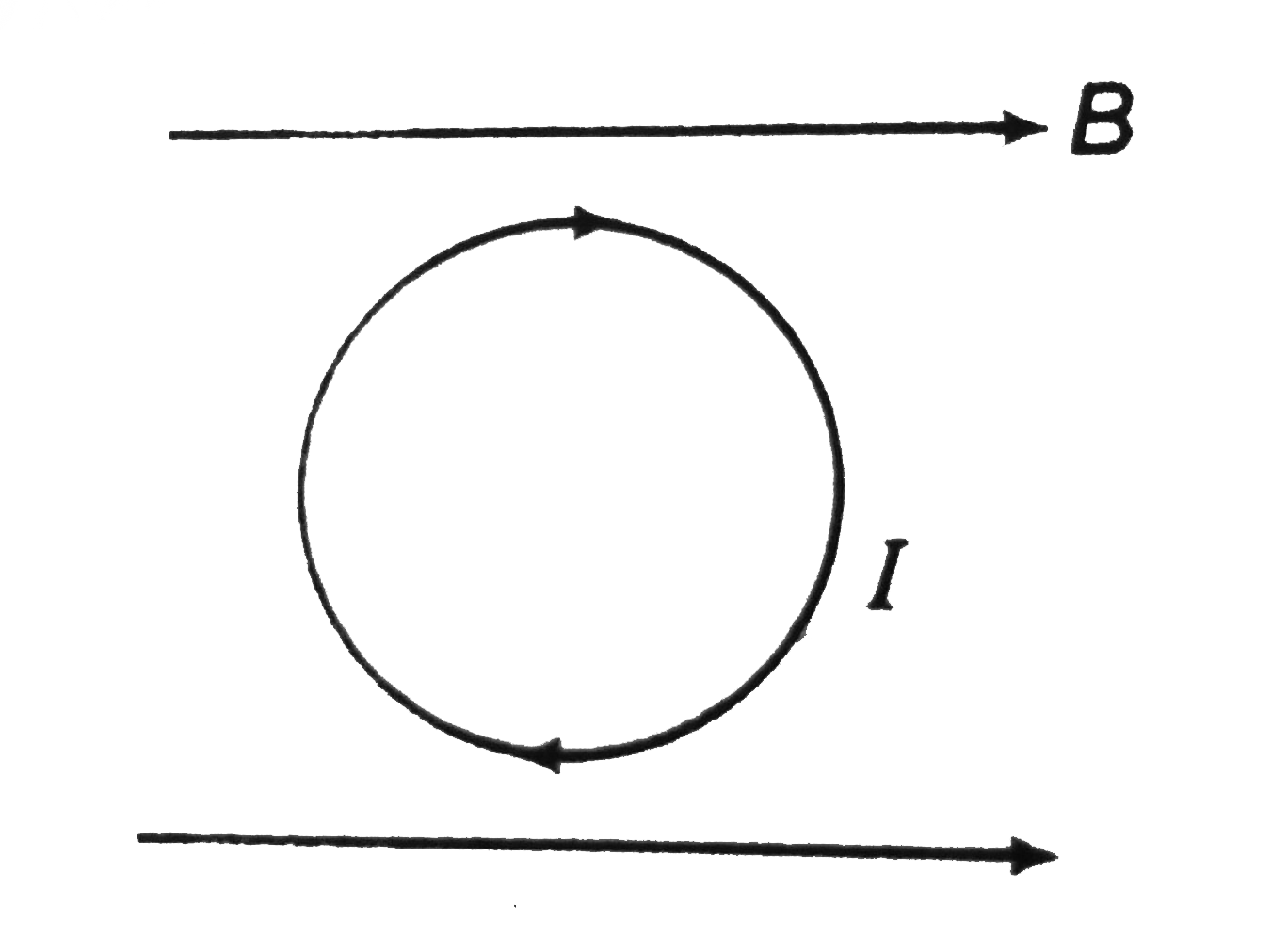
View SolutionAssertion Net torque in the current carrying loop placed in a uniform magnetic field (pointing inwards) is zero.

Reasonl Magnetic moment (M) is inwards.
View Solution