Question

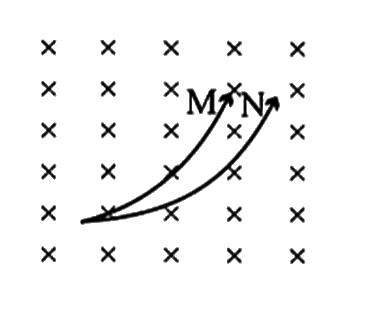
Two ions have equal masses but one is singly- ionized and the other is doubly- ionized. They are pojected from the same place in a uniform magnetic field with the same velocity perpendicular to the field.

Explanation

To solve the problem, we need to analyze the motion of two ions in a uniform magnetic field. The ions have the same mass but different charges due to their ionization states. Let's denote the following:

- Mass of both ions: $$m$$
- Velocity of both ions: $$v$$
- Magnetic field strength: $$B$$
- Charge of the singly ionized ion: $$q$$
- Charge of the doubly ionized ion: $$2q$$

1. Understanding the Forces:
When a charged particle moves in a magnetic field, it experiences a magnetic force that acts as the centripetal force required to keep it moving in a circular path. The magnetic force \( F_B \) is given by:
\( F_B = qvB \)
The centripetal force \( F_C \) required to keep the particle in circular motion is given by:
\( F_C = \frac{mv^2}{R} \)
where \( R \) is the radius of the circular path.

2. Setting Forces Equal:
For the ions to move in a circular path, the magnetic force must equal the centripetal force:
\( qvB = \frac{mv^2}{R} \)

3. Rearranging for Radius:
Rearranging the equation to solve for the radius \( R \):
\( R = \frac{mv}{qB} \)

4. Calculating the Radius for Each Ion:
- For the singly ionized ion (charge \( q \)):
\( R_1 = \frac{mv}{qB} \)
- For the doubly ionized ion (charge \( 2q \)):
\( R_2 = \frac{mv}{2qB} \)

5. Comparing the Radii:
From the equations for \( R_1 \) and \( R_2 \), we can see that:
\( R_2 = \frac{1}{2} R_1 \)
This indicates that the radius of the path of the doubly ionized ion is half that of the singly ionized ion.

Conclusion:
The radius of the circular path for the singly ionized ion is twice that of the doubly ionized ion. Thus, the singly ionized ion will travel in a larger circle compared to the doubly ionized ion when projected in the same magnetic field with the same velocity.