A positively charged particle is moving along the positive X-axis.You want to apply a magnetic field for a short time so that the particle may reverse its direction and move parallel to the negative X-axis.This can be done be applying the magnetic field along.
y-axis
z-axis
y-axis only
z-axis only
The correct Answer is:(a) (b)
To solve the problem of reversing the direction of a positively charged particle moving along the positive X-axis so that it moves parallel to the negative X-axis, we can follow these steps:
1. Understanding the Motion of the Charged Particle:
- The positively charged particle is initially moving in the positive X direction. We need to apply a magnetic field to change its direction to the negative X direction.
2. Using the Right-Hand Rule:
- The force acting on a charged particle moving in a magnetic field is given by the Lorentz force law:
→F=q(→v×→B)
where q is the charge, →v is the velocity vector, and →B is the magnetic field vector.
3. Determining the Required Force Direction:
- To reverse the direction of the particle from positive X to negative X, the magnetic force must act in the negative X direction.
4. Choosing the Direction of the Magnetic Field:
- If we apply the magnetic field in the positive Y direction (→B along +Y), we can use the right-hand rule:
- Point your fingers in the direction of the velocity (positive X).
- Curl your fingers in the direction of the magnetic field (positive Y).
- Your thumb will point in the direction of the force, which will be in the negative Z direction.
- This force will cause the particle to move in the negative Z direction, eventually allowing it to turn and move parallel to the negative X direction.
5. Verifying Other Directions:
- If we apply the magnetic field in the negative Y direction (→B along -Y), the force will act in the positive Z direction, which will also allow the particle to turn and move parallel to the negative X direction.
- If we apply the magnetic field in the Z direction (either positive or negative), the force will act in the Y direction, which will not help in reversing the direction of the particle effectively.
Conclusion:
To reverse the direction of the positively charged particle moving along the positive X-axis to move parallel to the negative X-axis, the magnetic field should be applied along the Y-axis (either positive or negative).
- The positively charged particle is initially moving in the positive X direction. We need to apply a magnetic field to change its direction to the negative X direction.
- The force acting on a charged particle moving in a magnetic field is given by the Lorentz force law:
→F=q(→v×→B)
where q is the charge, →v is the velocity vector, and →B is the magnetic field vector.
- To reverse the direction of the particle from positive X to negative X, the magnetic force must act in the negative X direction.
- If we apply the magnetic field in the positive Y direction (→B along +Y), we can use the right-hand rule:
- Point your fingers in the direction of the velocity (positive X).
- Curl your fingers in the direction of the magnetic field (positive Y).
- Your thumb will point in the direction of the force, which will be in the negative Z direction.
- This force will cause the particle to move in the negative Z direction, eventually allowing it to turn and move parallel to the negative X direction.
- If we apply the magnetic field in the negative Y direction (→B along -Y), the force will act in the positive Z direction, which will also allow the particle to turn and move parallel to the negative X direction.
- If we apply the magnetic field in the Z direction (either positive or negative), the force will act in the Y direction, which will not help in reversing the direction of the particle effectively.
To reverse the direction of the positively charged particle moving along the positive X-axis to move parallel to the negative X-axis, the magnetic field should be applied along the Y-axis (either positive or negative).
Topper's Solved these Questions
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - QUESTIONS FOR SHORT ASNWER
10 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
Similar Questions
An electron is moving along the positive x-axis. You want to apply a magnetic field for a short time so that the electron may reverse its direction and move parallel to the nagative x-axis. This can be done by applying the magnetic field along
View SolutionA moving charged particle q travelling along the positive X-axis enters a uniform magnetic field B. When will the force acting on q be maximum?
View SolutionA positively charged particle is moving along the positive x-axis in a unifom electric field→E=E0ˆj and magnetic field →B=B0ˆk (where E0 and B0 are positive constants), then
View SolutionA positively charged particle moving due east enters a region of uniform magnetic field directed vertically upwards. The partical will be
View SolutionA positively charged particle moving along x-axis with a certain velocity enters a uniform electric field directed along positive y-axis. Its
View SolutionA charged particle is moved along a magnetic field line. The magnetic force on the particle is
View SolutionA proton is moving along the negative direction of X-axis in a magnetic field directed along the positive direction of Y-axis. The proton will be deflected along the negative direction of
View SolutionA proton is moved along a magnetic field line.The magnetic force on the particle is
View SolutionA magnetic of magnetic moment placed along the X-axis in an magnet field .Find the torque acting on the magnetic field
View SolutionA particle is moving along the x-axis and its position-time graph is shown. Determine the sign of acceleration.
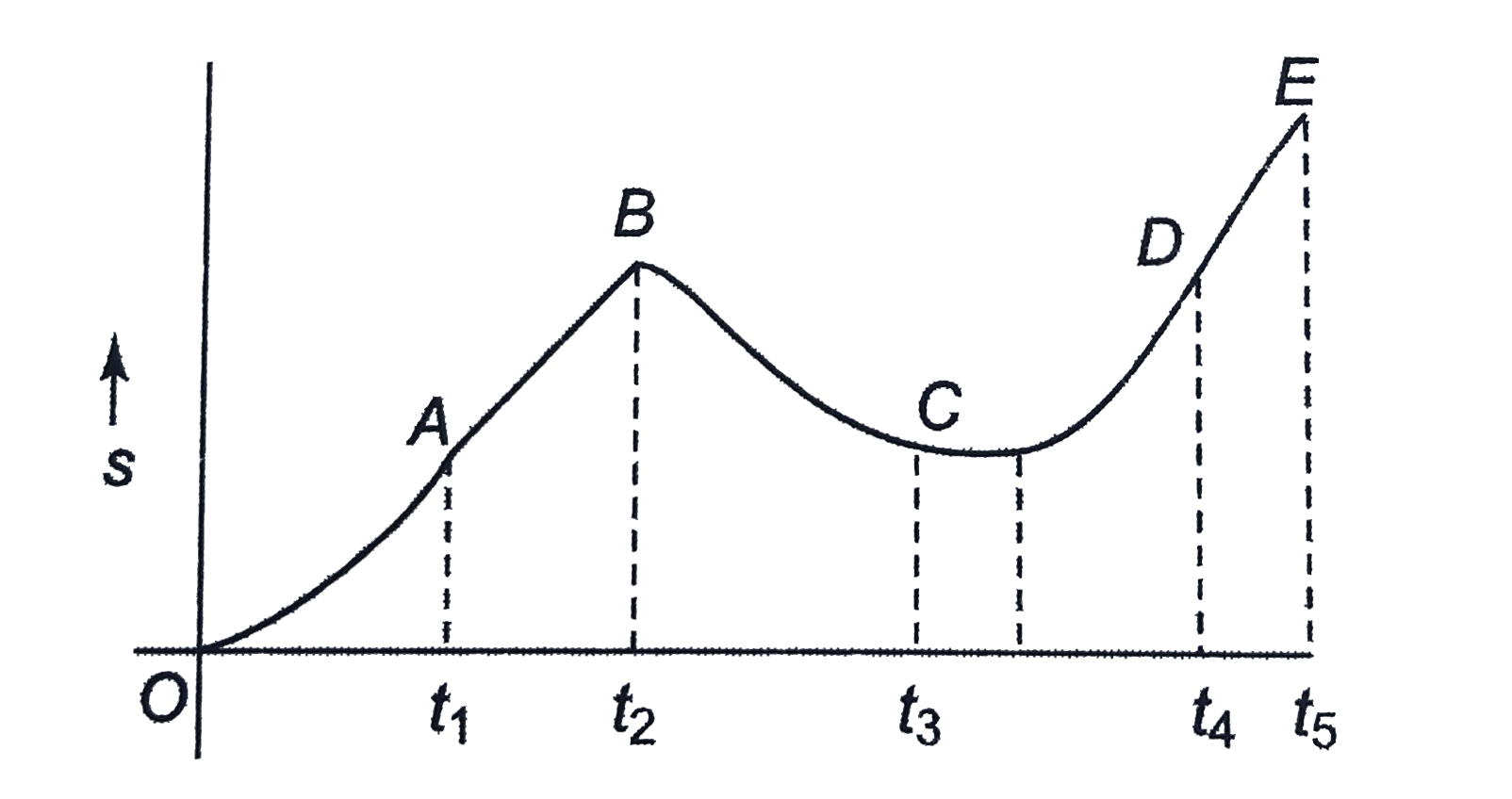
View Solution
