An electron having a kinetic energy of 100eV circulates in a path of radius 10cm in a magnetic field. Find the magnetic field and the number of revolutons per second made by the electron.
To solve the question, we need to find the magnetic field (B) and the number of revolutions per second (f) made by an electron with a given kinetic energy (KE) and radius of circular motion (r).
Step 1: Convert Kinetic Energy to Joules
The kinetic energy (KE) of the electron is given as 100 eV. We need to convert this energy into joules. The conversion factor is:
1 eV = 1.6 × 10^-19 J.
So, the kinetic energy in joules is:
KE=100eV×1.6×10−19J/eV=1.6×10−17J.
Step 2: Calculate the Velocity of the Electron
The kinetic energy of the electron is also given by the formula:
KE=12mv2,
where m is the mass of the electron (approximately 9.11×10−31kg) and v is its velocity.
Rearranging the formula to solve for v:
v=√2×KEm.
Substituting the values:
v=√2×1.6×10−17J9.11×10−31kg≈√3.51×1013≈5.93×106m/s.
Step 3: Use the Centripetal Force Equation
In a magnetic field, the centripetal force required to keep the electron moving in a circular path is provided by the magnetic force. The magnetic force F on a charged particle moving in a magnetic field is given by:
F=qvB,
where q is the charge of the electron (approximately 1.6×10−19C).
The centripetal force required for circular motion is given by:
F=mv2r.
Setting the two forces equal to each other:
qvB=mv2r.
Step 4: Solve for the Magnetic Field (B)
Rearranging the equation to solve for B:
B=mvqr.
Substituting the known values:
B=(9.11×10−31kg)(5.93×106m/s)(1.6×10−19C)(0.1m).
Calculating B:
B≈5.39×10−241.6×10−20≈0.0337T(Tesla).
Step 5: Calculate the Number of Revolutions per Second (f)
The number of revolutions per second (frequency) can be calculated using the formula:
f=v2πr.
Substituting the values:
f=5.93×106m/s2π(0.1m)≈5.93×1060.628≈9.45×106rev/s.
Final Answers
1. The magnetic field B is approximately 0.0337 T.
2. The number of revolutions per second f is approximately 9.45 million rev/s.
The kinetic energy (KE) of the electron is given as 100 eV. We need to convert this energy into joules. The conversion factor is:
1 eV = 1.6 × 10^-19 J.
KE=100eV×1.6×10−19J/eV=1.6×10−17J.
The kinetic energy of the electron is also given by the formula:
KE=12mv2,
where m is the mass of the electron (approximately 9.11×10−31kg) and v is its velocity.
v=√2×KEm.
v=√2×1.6×10−17J9.11×10−31kg≈√3.51×1013≈5.93×106m/s.
In a magnetic field, the centripetal force required to keep the electron moving in a circular path is provided by the magnetic force. The magnetic force F on a charged particle moving in a magnetic field is given by:
F=qvB,
where q is the charge of the electron (approximately 1.6×10−19C).
F=mv2r.
qvB=mv2r.
Rearranging the equation to solve for B:
B=mvqr.
B=(9.11×10−31kg)(5.93×106m/s)(1.6×10−19C)(0.1m).
B≈5.39×10−241.6×10−20≈0.0337T(Tesla).
The number of revolutions per second (frequency) can be calculated using the formula:
f=v2πr.
f=5.93×106m/s2π(0.1m)≈5.93×1060.628≈9.45×106rev/s.
1. The magnetic field B is approximately 0.0337 T.
2. The number of revolutions per second f is approximately 9.45 million rev/s.
Topper's Solved these Questions
- MAGNETIC FIELDBook:HC VERMA ENGLISHChapter:MAGNETIC FIELDExercise:QUESTIONS FOR SHORT ASNWER
Explore 10 Videos
- MAGNETIC FIELDBook:HC VERMA ENGLISHChapter:MAGNETIC FIELDExercise:objective2
Explore 9 Videos
- MAGNETIC FIELDBook:HC VERMA ENGLISHChapter:MAGNETIC FIELDExercise:objective 1
Explore 10 Videos
- LIGHT WAVESBook:HC VERMA ENGLISHChapter:LIGHT WAVESExercise:Question for short Answer
Explore 11 Videos
- MAGNETIC FIELD DUE TO CURRENTBook:HC VERMA ENGLISHChapter:MAGNETIC FIELD DUE TO CURRENTExercise:questions for short answer
Explore 12 Videos
Similar Questions
An electron having kinetic energy 10eV is circulating in a path of radius 0.1 m in an external magnetic field of intensity 10−4T. The speed of the electron will be
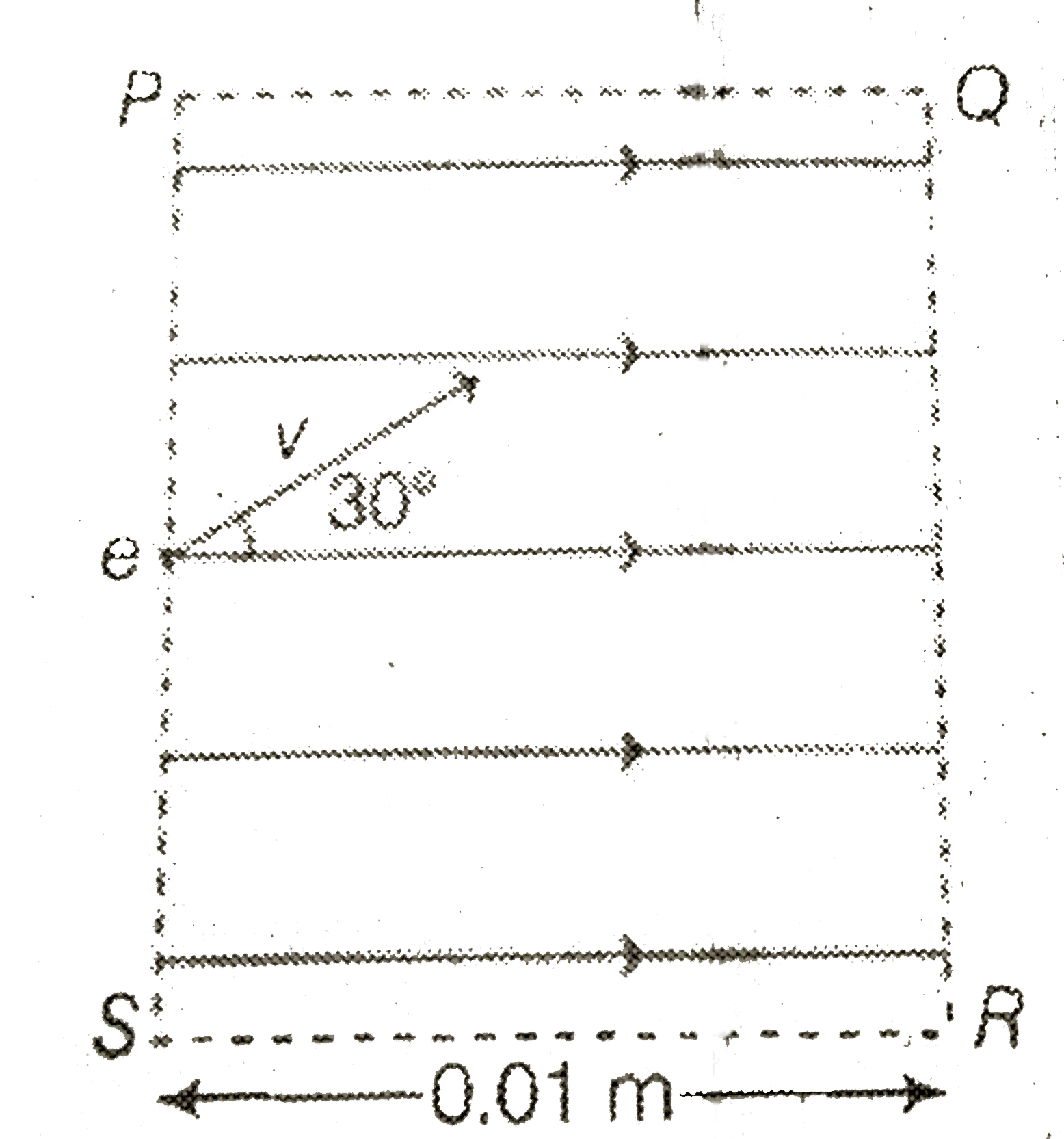
View SolutionRefer to the figure. Rectangle PQRS represents the cross section of a uniform magnetic field region of 0.20 T. An electron is projected at a speed of V=2.0×106m/s into the region at an angle of 30∘ to the direction of the mangetic field. The length of the magnetic field region is 0.01 m. Find the number of revolutions made by the electron before it leaves the magnetic field region.
View Solution
Knowledge Check
A circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
A2.01×10−3TB5.64×10−3TC2.64×10−3TD5.64×10−3TA moving electron enters a uniform and perpendicular magnetic field. Inside the magnetic field, the electron travels along :
Aa straight lineBa parabolaCa circleDa hyperbola
An electron is moving on a circular path of radius r with speed v in a transverse magnetic field B. e/m for it will be
View SolutionAn electron makes (3×105) revolutions per second in a circle of radius 0.5 angstrom. Find the magnetic field B at the centre of the circle.
View SolutionAn electron moving in a circular orbit of radius makes n rotations per second. The magnetic field produced at the centre has magnitude :
View SolutionA moving electron enters a uniform and perpendicular magnetic field. Inside the magnetic field, the electron travels along :
View SolutionAn electron moving in a circular orbit of radius r makes n rotation per second. The magnetic field produced at the centre has magnitude
View SolutionA proton carrying 1MeV kinetic energy is moving in a circular path of radius R in uniform magnetic field. What should be the energy of an α− particle to describe a circle of the same radius in the same field?
View Solution
