Fe^+ ions are accelerated through a potential difference of 500 V and are injected normally into a homogeneous magnetic field B of strength 20.0 m T. Find the radius of the circular paths followed by the isotopes with mass numbers 57 and 58. Take the mass of an ion=A(1.6X10−27 kg where A is the mass number.
To solve the problem of finding the radius of the circular paths followed by Fe^+ ions with mass numbers 57 and 58 when accelerated through a potential difference of 500 V and injected into a magnetic field of strength 20.0 mT, we can follow these steps:
Step 1: Determine the mass of the ions
The mass of an ion is given by the formula:
m=A×(1.6×10−27) kg
where A is the mass number.
For the isotope with mass number 57:
m1=57×(1.6×10−27)=9.12×10−26 kg
For the isotope with mass number 58:
m2=58×(1.6×10−27)=9.28×10−26 kg
Step 2: Calculate the charge of the ions
The charge of a single Fe^+ ion is:
Q=1.6×10−19 C
Step 3: Calculate the velocity of the ions after acceleration
The kinetic energy gained by the ions when accelerated through a potential difference V is given by:
KE=QV
Substituting the values:
KE=(1.6×10−19)×500=8.0×10−17 J
The kinetic energy can also be expressed in terms of mass and velocity:
KE=12mv2
Setting these equal gives:
12mv2=QV
Solving for v:
v=√2QVm
Step 4: Calculate the radius of the circular path in the magnetic field
The radius r of the circular path of a charged particle moving in a magnetic field is given by:
r=mvQB
Substituting for v:
r=m√2QVmQB=√2QVmQB=√2VmB
Step 5: Calculate the radius for both isotopes
For isotope 1 (mass number 57):
r1=√2×500×(9.12×10−26)20×10−3
Calculating this gives:
r1=√9.12×10−2320×10−3
r1=3.02×10−1120×10−3=1.51×10−6 m=1.51 cm
For isotope 2 (mass number 58):
r2=√2×500×(9.28×10−26)20×10−3
Calculating this gives:
r2=√9.28×10−2320×10−3
r2=3.05×10−1120×10−3=1.52×10−6 m=1.52 cm
Final Answers
- The radius of the circular path for the isotope with mass number 57 is approximately 1.51 cm.
- The radius of the circular path for the isotope with mass number 58 is approximately 1.52 cm.
The mass of an ion is given by the formula:
m=A×(1.6×10−27) kg
where A is the mass number.
m1=57×(1.6×10−27)=9.12×10−26 kg
m2=58×(1.6×10−27)=9.28×10−26 kg
The charge of a single Fe^+ ion is:
Q=1.6×10−19 C
The kinetic energy gained by the ions when accelerated through a potential difference V is given by:
KE=QV
Substituting the values:
KE=(1.6×10−19)×500=8.0×10−17 J
KE=12mv2
Setting these equal gives:
12mv2=QV
Solving for v:
v=√2QVm
The radius r of the circular path of a charged particle moving in a magnetic field is given by:
r=mvQB
Substituting for v:
r=m√2QVmQB=√2QVmQB=√2VmB
For isotope 1 (mass number 57):
r1=√2×500×(9.12×10−26)20×10−3
Calculating this gives:
r1=√9.12×10−2320×10−3
r1=3.02×10−1120×10−3=1.51×10−6 m=1.51 cm
r2=√2×500×(9.28×10−26)20×10−3
Calculating this gives:
r2=√9.28×10−2320×10−3
r2=3.05×10−1120×10−3=1.52×10−6 m=1.52 cm
- The radius of the circular path for the isotope with mass number 57 is approximately 1.51 cm.
- The radius of the circular path for the isotope with mass number 58 is approximately 1.52 cm.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - QUESTIONS FOR SHORT ASNWER10videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective 110videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer12videos
MAGNETIC FIELD DUE TO CURRENT
Similar Questions
An electron of mass 'm' is accelerated through a potential difference of V and then it enters a magnetic field of inductionB. Normal to the lines of force. Then the radius of the circular path is
View SolutionA charged particle is accelerated thrught a potential difference of 12 kV and acquires a speed of 1.0X106ms−1. It is then injected perpendiuclarly into a magnetic field of strenght 0.2 T. find the radius of the circle described by it.
View SolutionAn electron of mass m and charge e is accelerated by a potential difference V. It then enters a uniform magnetic field B applied perpendicular to its path. The radius of the circular path of the electron is
View SolutionAn electron is accelerated through a PD of 100V and then enters a region where it is moving perpendiculasr to a magnetic fiedl B=0.2T. Find the radius of the circular path. Repeat this problem for a proton.
View SolutionSingly charged magnesium (A=24) ions are accelerated to kinetic energy 2keV and are projected perpendicularly into a magnetic field B of magnitude 0.6 T. (a) Find the radius of the circle formed by the ions. (b) If there are also singly charged ions of the isotope magnesium.26, what would be the radius for these particles?
View SolutionA narrow beam of singley charged carbon ions, moving at a constant velocity of 6.0X104ms−1, is sent perpendicularly in a rectangular region having uniform magnetic field B=0.5 T . It is found that two beams emerge from the field in the backward derection, the separations from the incident beam being 3.0 cm and 3.5cm. Identify the isotopes persent in the ion beam. Take the mass of an ion = A(1.6X10−27 kg, where A is the mass number.
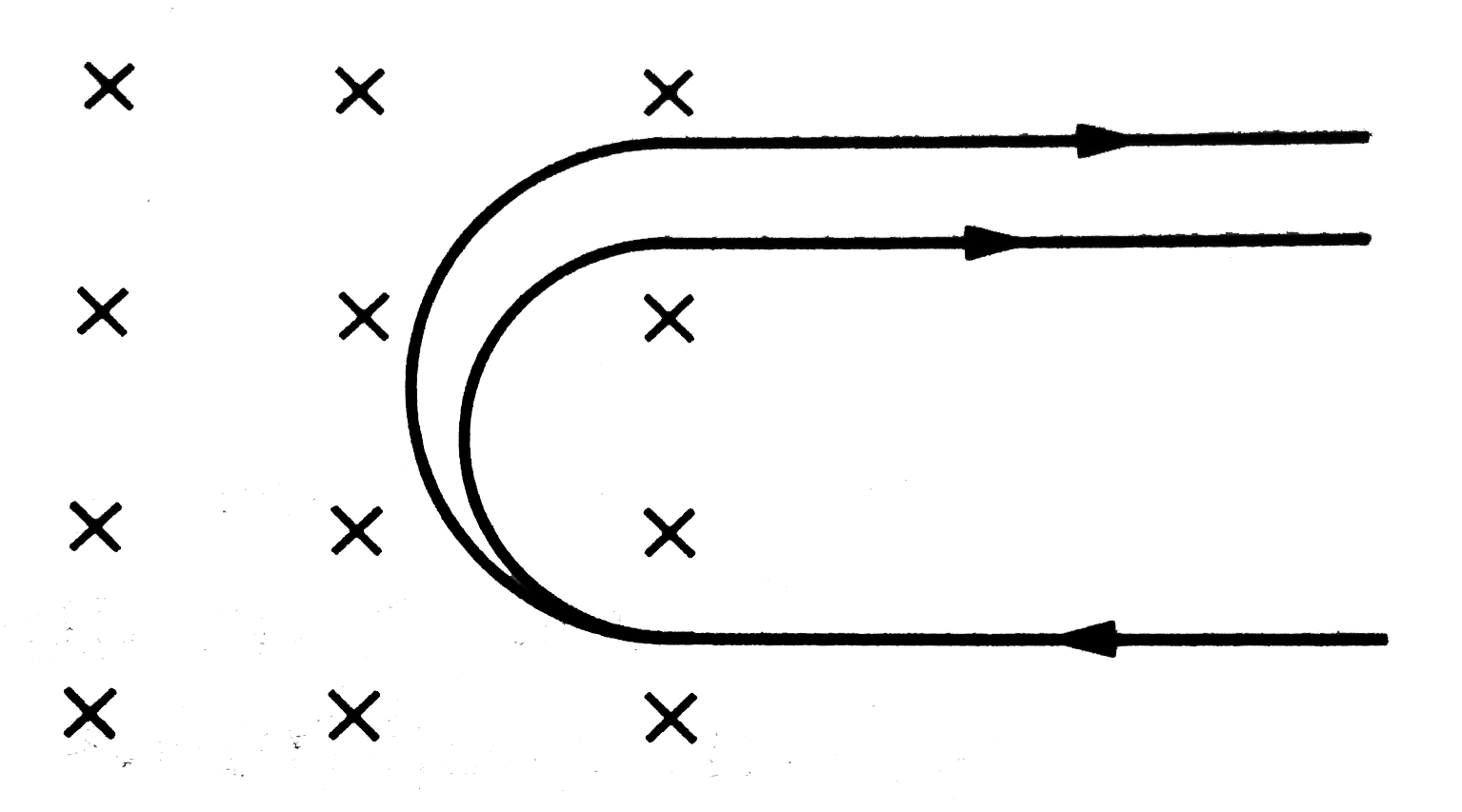 View Solution
View SolutionA particle of mass m carrying charge q is accelerated by a potential difference V. It enters perpendicularly in a region of uniform magnetic field B and executes circular arc of radius R, then qm equals
View SolutionA charged particle of mass m and charge q is accelerated through a potential differences of V volts. It enters of uniform magnetic field B which is directed perpendicular to the direction of motion of the particle. The particle will move on a circular path of radius
View SolutionA charged particle of mass m and charge q is accelerated through a potential difference of V volts. It enters a region of uniform magnetic field which is directed perpendicular to the direction of motion of the particle. Find the radius of circular path moved by the particle in magnetic field.
View SolutionA proton projected in a magnetic field of 0.020 T travels along a helical path of radius 5.0 cm and pitch 20 cm. Find the components of the velocity of the proton along and perpendicular to the magnetic field. Take the mass of the proton=1.6X10−27kg.
View Solution

