A conducting rod is moved with a constant velocity v in a magnetic field. A potential difference appears across the two ends
if vec v|| vec l
if vec v ||vec B
if vec l || vec B
none of these.
The correct Answer is:D
To solve the problem of a conducting rod moving in a magnetic field and generating a potential difference across its ends, we can follow these steps:
1. Identify the Components:
- Let the length of the conducting rod be L.
- The rod is moving with a constant velocity v.
- The magnetic field B is present in the region where the rod is moving.
2. Understanding the EMF Generation:
- When a conducting rod moves through a magnetic field, an electromotive force (EMF) is induced across its ends.
- The EMF (E) can be calculated using the formula:
E=v⋅B⋅L⋅sin(θ)
where θ is the angle between the velocity vector v and the magnetic field vector B.
3. Conditions for Non-Zero EMF:
- For the EMF to be non-zero, the vectors v, B, and L must not be parallel. This means:
- v must be perpendicular to B, or
- v must be perpendicular to L, or
- B must be perpendicular to L.
4. Analyzing the Given Options:
- If v is parallel to L, then sin(0)=0 and EMF will be zero.
- If v is parallel to B, then again sin(0)=0 and EMF will be zero.
- Therefore, for EMF to exist, none of these conditions can hold true.
5. Conclusion:
- Since the EMF exists between the two ends of the rod, the only valid conclusion is that the conditions for EMF generation are not satisfied by the given options. Hence, the answer is that none of the options provided are correct.
Final Answer:
The answer is: None of these.
- Let the length of the conducting rod be L.
- The rod is moving with a constant velocity v.
- The magnetic field B is present in the region where the rod is moving.
- When a conducting rod moves through a magnetic field, an electromotive force (EMF) is induced across its ends.
- The EMF (E) can be calculated using the formula:
E=v⋅B⋅L⋅sin(θ)
where θ is the angle between the velocity vector v and the magnetic field vector B.
- For the EMF to be non-zero, the vectors v, B, and L must not be parallel. This means:
- v must be perpendicular to B, or
- v must be perpendicular to L, or
- B must be perpendicular to L.
- If v is parallel to L, then sin(0)=0 and EMF will be zero.
- If v is parallel to B, then again sin(0)=0 and EMF will be zero.
- Therefore, for EMF to exist, none of these conditions can hold true.
- Since the EMF exists between the two ends of the rod, the only valid conclusion is that the conditions for EMF generation are not satisfied by the given options. Hence, the answer is that none of the options provided are correct.
The answer is: None of these.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
98 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 1
11 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
Similar Questions
A rod AB moves with a uniform velocity v in a uniform magnetic field as shown in figure

View SolutionA circular loop of radius r moves with a constant velocity v in a region with uniform magnetic field B. Calculate the potential difference between two points (A,B), (C,D), and (E,F) located on the loop.

View Solution
Knowledge Check
If an electron is moving with velocity v produces a magnetic field →B, then
Athe direction of field →B will be same as the direction of velocity →v.Bthe direction of field →B will be opposite to the direction of velocity →v.Cthe direction of field →B will be perpendicular to the direction of velocity →v.Dthe direction of field →B does not depend upon the direction of velocity →v.
A conducing rod of length l is falling with a velocity v perpendicular to a unifrorm horizontal magnetic field B . The potential difference between its two ends will be
View SolutionA conducting rod of resistance r moves uniformly with a constant speed v in a uniform magnetic field. If the rod keeps moving uniformly, then the amount of force required is
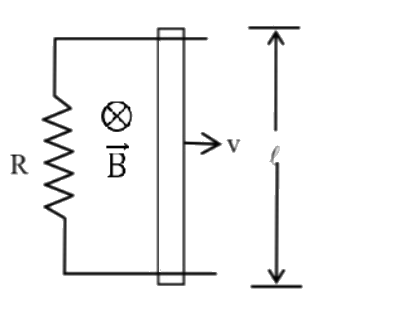
View SolutionA small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __

A. Then the end X of the rod become positively charged
B. The end Y of the rod become positively charged
C. The entire rod is unevenly charged
D. The rod become hot due to joule heating
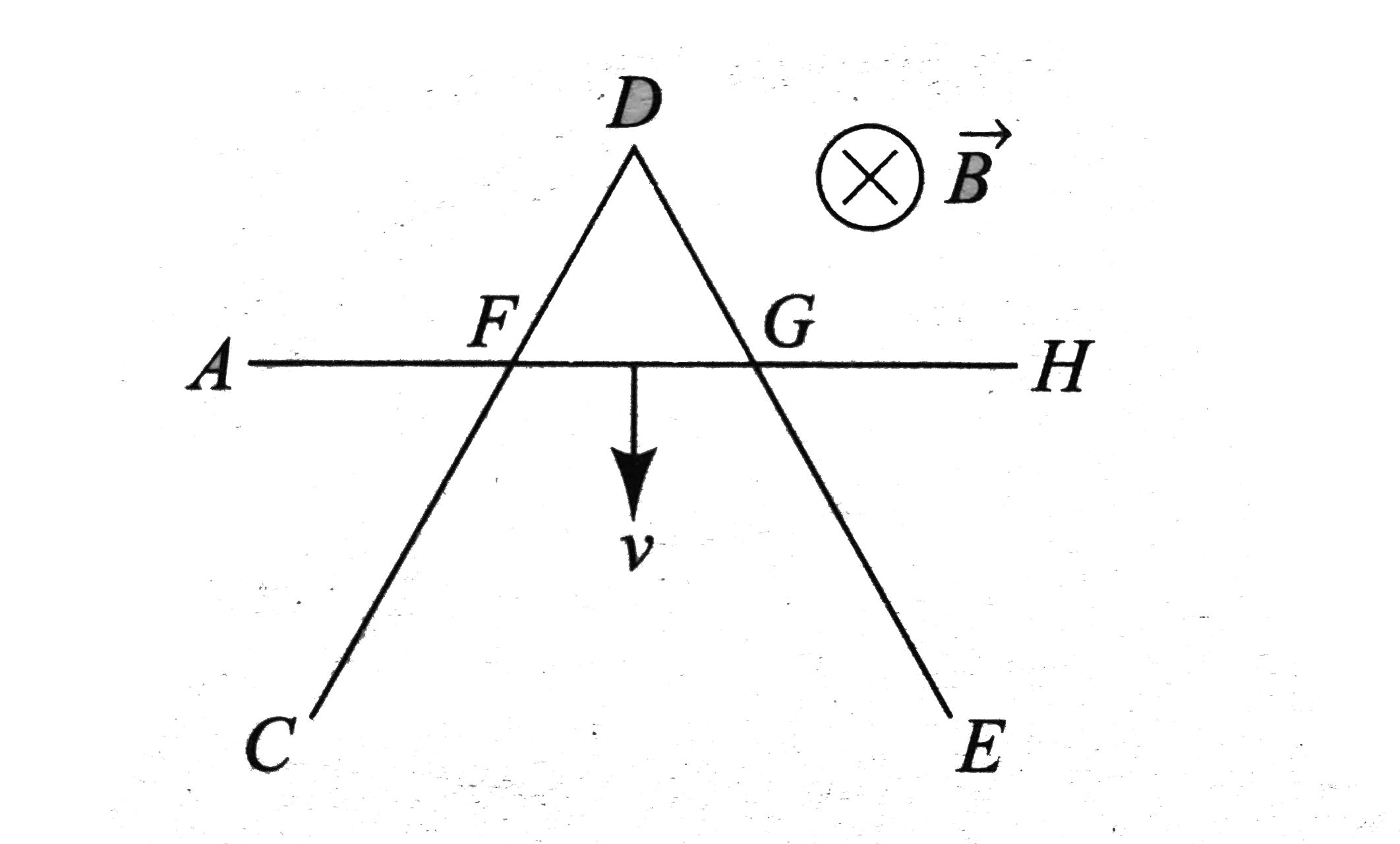
View SolutionA long conducting wire AH is moved over a conducting triangular wire CDE with a constant velocity v in a uniform magnetic field →B directed into the plane of the paper. Resistance per unit length of each wire is ρ. Then
View SolutionA metallic conductor of irregular cross-section is as shown in the figure. A constant potential difference is applied across the ends (1) and (2). Then :

View SolutionA small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __

View SolutionIn the figure shown a T−shaped conductor moves with constant angular velocity ω in a plane perpendicular to uniform magnetic field B. The potential difference VA−VB is

View Solution
