A conducting wire ab of length l, resistance r and mass m starts sliding at t = 0 down a smooth, vertical, thick pair of connected rails as shown in . A uniform magnetic field B exists in the space in a diraction perpendicular to the plane of the rails. (a) Write the induced emf in the loop at an instant t when the speed of the wire is v. (b) what would be the magnitude and direction of the induced current in the wire? (c) Find the downward acceleration of the wire at this instant. (d) After sufficient time, the wire starts moving with a constant velocity. Find this velocity v_m. (e) Find the velocity of the wire as a function of time. (f) Find the displacement of the wire as a functong of time. (g) Show that the rate of heat developed inte wire is equal to the rate at which the gravitational potential energy is decreased after steady state is reached.
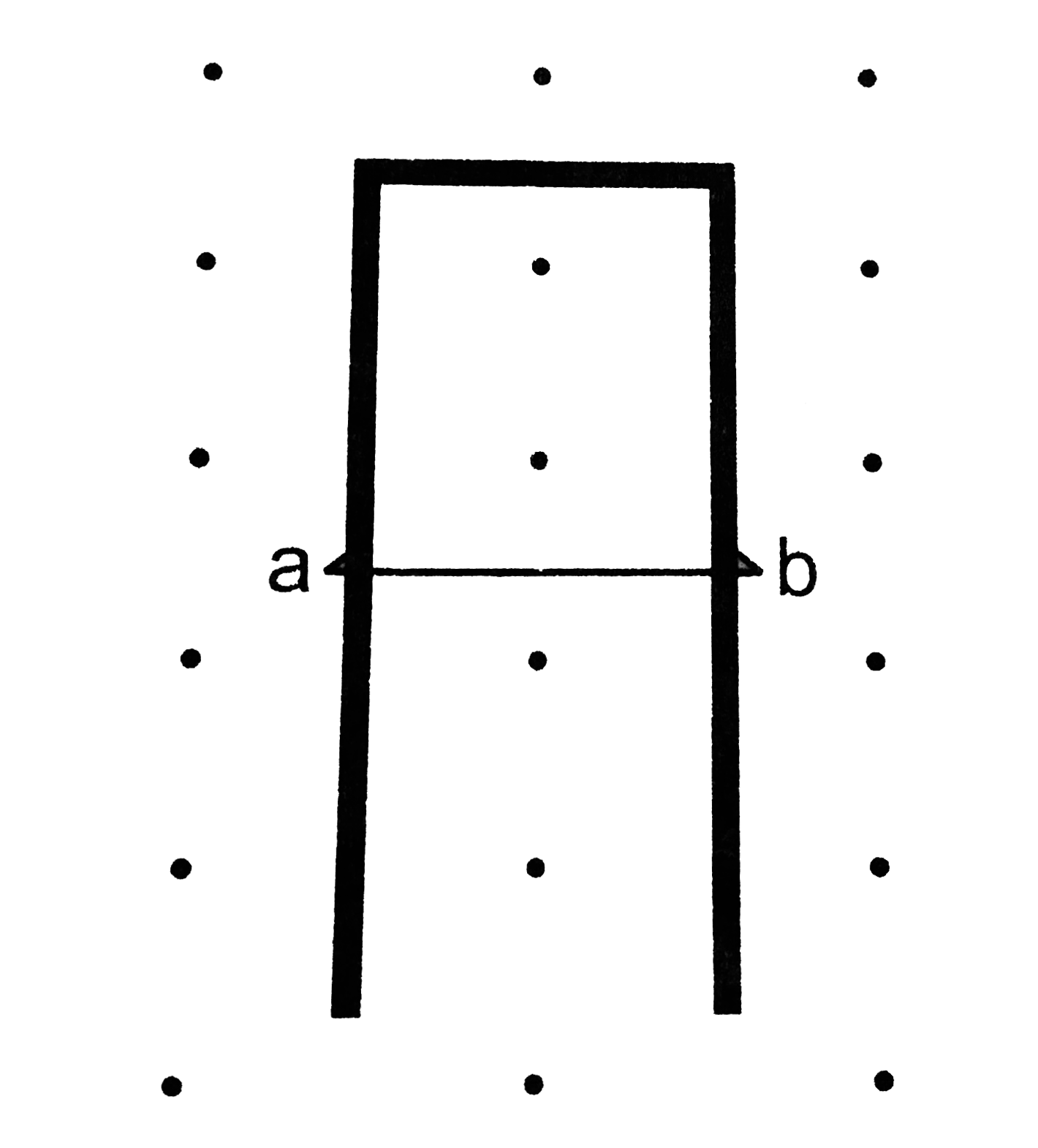
(a) when the speed the speed of wire is v
emf developed =Blv<br>(b) Induced current is the wire =(Blv)/R<br>(from b to a )<br>(c ) Downwards acceleration of the wire<br>=(mg-F)/m due to the current <br>=(ilB)/(m)=g=(B^2l^2v)/(Rm)<br>(d) let the start moving with constant velocity then acceleration =0<br>(B^2l^2v_m)/(Rm)=g<br> implies V_m=(GrM)/(B^2l^2)<br>(e) since (dv)/(dt)=a<br>implies (dv)/(dt)=((mg-B^2l^2v//R)/m) implies (dv)/((mg-B^2l^2v//R)/(m))=dt<br>int_(0)^(v)(m dv)/(mg-(B^2l^2v/R)/(m))=int_(0)^(v)dt<br>implies (m)/((B^2l^2v)/(R))[log (mg-((B^2l^2v)/(R))]_(0)^(v)=t<br> implies(-mR)/(B^2l^2)[log (mg-(B^2l^2v)/(R))-log(mg)]=t<br>⇒log⎡⎢⎣mg−B2l2vRmg⎤⎥⎦=−tB2l2mr
=log[1−B2l2vRmg]=−tB2l2mr
⇒1−(B2l2v)(Rmg)=e−tB2l2mr
⇒(1−e(−tB2l2))=B2l2vRmg
v−RmgB2l2(1−e(−tB2l2))
⇒v=vm(1−e−gtvm)[∴vm=RmgB2l2]
(f)sincedsdt=v
∫ds=∫v.dt
s=vm(1−e−gtvm)
=vm.(t+vmg.e−gtvm)
=(vmt+(vm)2ge−gtvm)−(Vm)2g
=vmt=(Vm)2g(1−e−gtvm)
(g) ddt(msg)=mg.dsdt
=mg.(vm)((1−e−gtvm)
dHdt=l2R=R.(lBvR)2
=l2B2v2R
=l2B2R.(Vm)2((1−e−gtvm)2
Aftersteadystatei.e..t→∞
ddt(msg)=mg(vm)ltbr>dHdt=l2B2R(vm)2
=(l^2B^2)/(r).(v_m).(mgR)/(l^2B^2)<br>Hence after steady state (d_H)/(dt)=(d)/(dt) mgs.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
Similar Questions
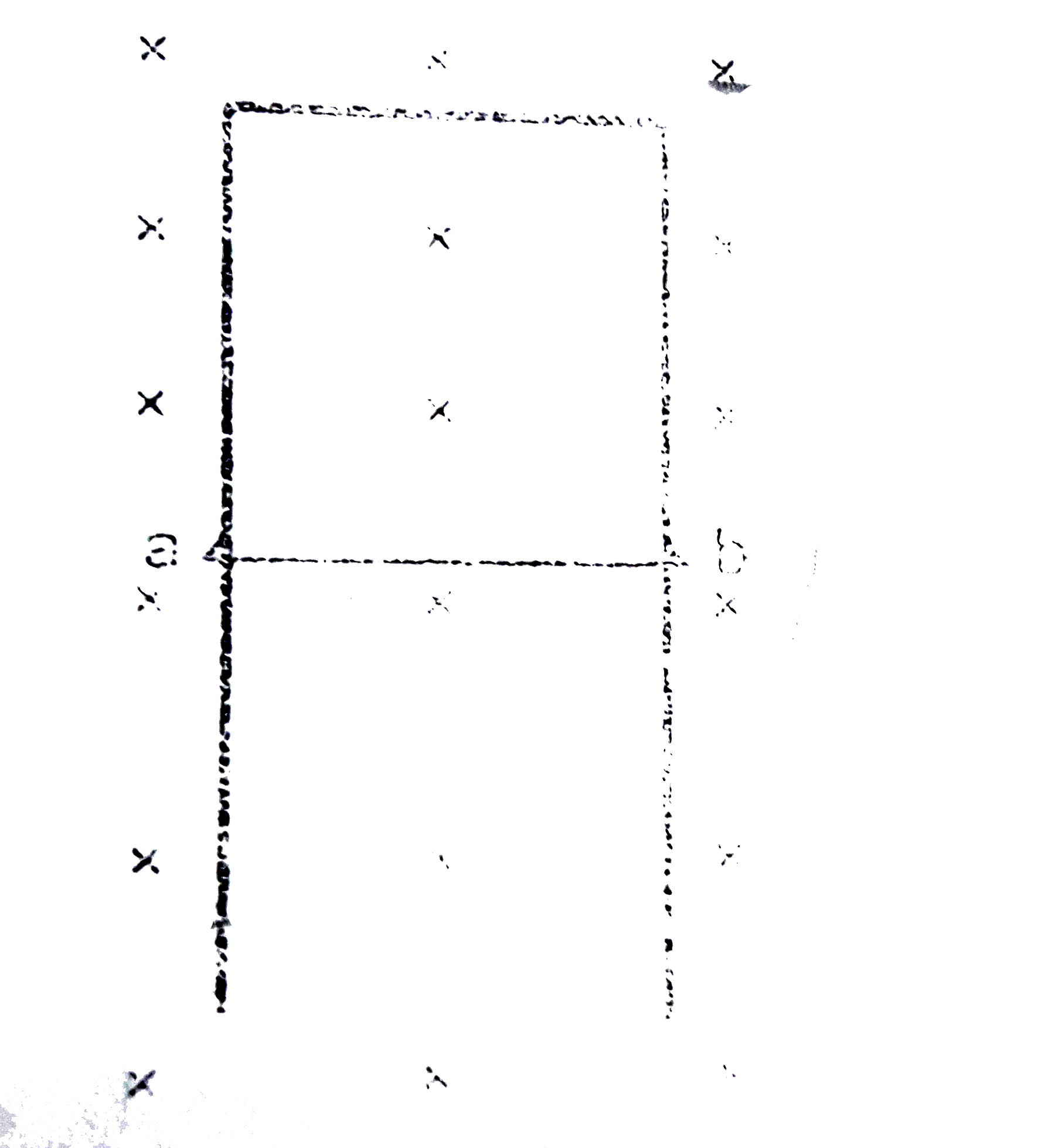
A copper wire ab of length l, resistance r and mass m starts sliding at t=0 down a smooth, vertical, thick pair of connected condcuting rails as shown in figure.A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct.
View SolutionA conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of

View Solution
Knowledge Check
A copper wire ab of length l, resistance r and mass m start sliding at t=0 down a smooth, vertical, thick pair of connected conducting rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct .
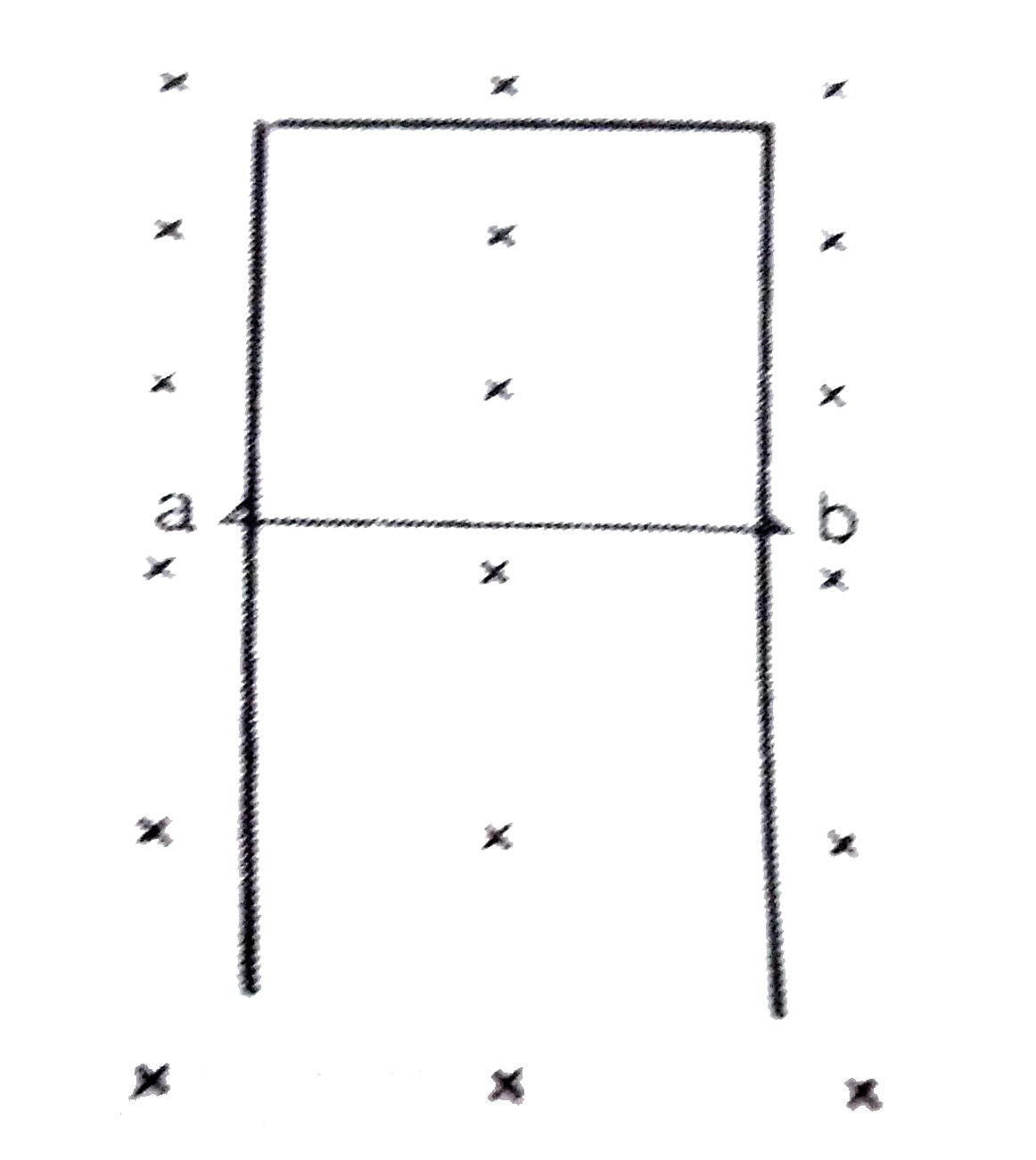 AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrvCThe velocity of the wire as a function of time vm(1−e−gt/vm),(wherevm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm),(wherevm=mgrB2l2)
AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrvCThe velocity of the wire as a function of time vm(1−e−gt/vm),(wherevm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm),(wherevm=mgrB2l2)A copper wire ab of length l, resistance r and mass m starts sliding at t=0 down a smooth, vertical, thick pair of connected condcuting rails as shown in figure.A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct.
 AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrv.CThe velocity of the wire as a function of time vm(1−e−gt/vm)(where vm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm)(where vm=mgrB2l2)
AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrv.CThe velocity of the wire as a function of time vm(1−e−gt/vm)(where vm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm)(where vm=mgrB2l2)A conducting wire ab of length l resistance r and mass m starts sliding down at t=0 on a smooth, vertical thick pair of connected rails as shown. The terminal speed of the wire is
 AmgRBlBmgrB2l2CmglB2r2DNone
AmgRBlBmgrB2l2CmglB2r2DNone
A conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of

View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
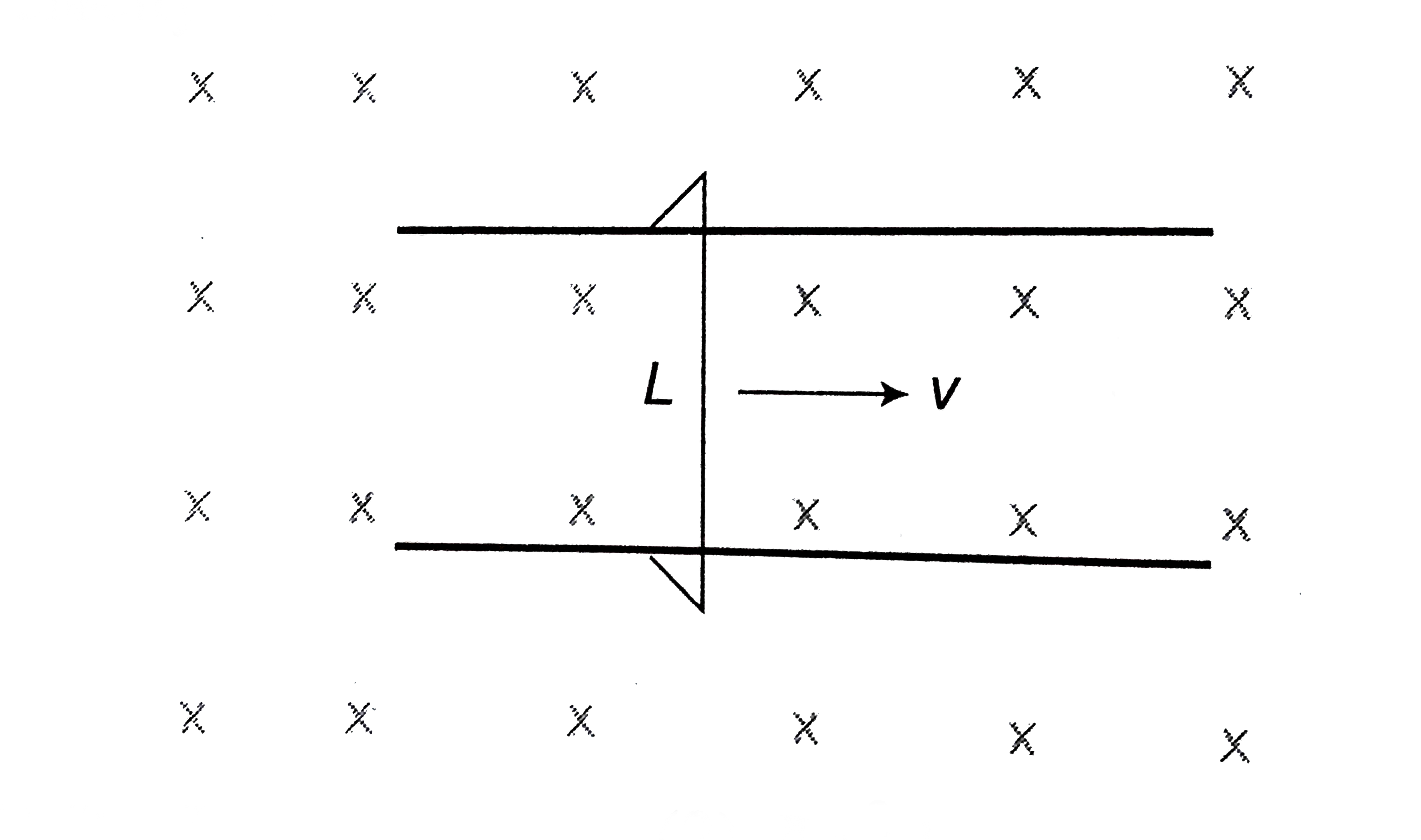
View SolutionShows a wire sliding on two parallel, conducting rails placed at a separaton l. A magnetic feld B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constatn velocity v ?

View SolutionA conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of

View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?

View Solution
