The work function of a thermionic emitter is . By what factor does the thermionic current increase if its temperature is raised from ?
To find the factor by which the thermionic current increases when the temperature is raised from 1500 K to 2000 K, we can follow these steps:
Step 1: Write the formula for thermionic current
The thermionic current I is given by the formula:
I=AsT2e−ϕkT
where:
- A is a constant depending on the metal,
- s is the surface area,
- T is the absolute temperature,
- ϕ is the work function,
- k is the Boltzmann constant.
Step 2: Define the currents at two temperatures
Let T1=1500K and T2=2000K.
The currents at these temperatures can be expressed as:
I1=AsT21e−ϕkT1
I2=AsT22e−ϕkT2
Step 3: Find the ratio of the currents
To find the factor by which the current increases, we take the ratio I2I1:
I2I1=AsT22e−ϕkT2AsT21e−ϕkT1
The constants A and s cancel out:
I2I1=T22T21e−ϕkT2+ϕkT1
Step 4: Simplify the exponent
This can be rewritten as:
I2I1=T22T21e−ϕk(1T2−1T1)
Step 5: Insert the values
Substituting T1=1500K, T2=2000K, ϕ=4.5eV, and k=8.617×10−5eV/K:
I2I1=(20001500)2e−4.58.617×10−5(12000−11500)
Step 6: Calculate the numerical values
1. Calculate (20001500)2=(43)2=169.
2. Calculate 12000−11500=3−46000=−16000.
3. Substitute into the exponent:
e−4.58.617×10−5(−16000)=e4.58.617×10−5×6000
Step 7: Final calculation
After calculating the exponent and multiplying by 169, we find:
I2I1≈10625
This means that the thermionic current increases by a factor of approximately 10625 when the temperature is raised from 1500 K to 2000 K.
---
The thermionic current I is given by the formula:
I=AsT2e−ϕkT
where:
- A is a constant depending on the metal,
- s is the surface area,
- T is the absolute temperature,
- ϕ is the work function,
- k is the Boltzmann constant.
Let T1=1500K and T2=2000K.
The currents at these temperatures can be expressed as:
I1=AsT21e−ϕkT1
I2=AsT22e−ϕkT2
To find the factor by which the current increases, we take the ratio I2I1:
I2I1=AsT22e−ϕkT2AsT21e−ϕkT1
The constants A and s cancel out:
I2I1=T22T21e−ϕkT2+ϕkT1
This can be rewritten as:
I2I1=T22T21e−ϕk(1T2−1T1)
Substituting T1=1500K, T2=2000K, ϕ=4.5eV, and k=8.617×10−5eV/K:
I2I1=(20001500)2e−4.58.617×10−5(12000−11500)
1. Calculate (20001500)2=(43)2=169.
2. Calculate 12000−11500=3−46000=−16000.
3. Substitute into the exponent:
e−4.58.617×10−5(−16000)=e4.58.617×10−5×6000
After calculating the exponent and multiplying by 169, we find:
I2I1≈10625
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Worked out example9videos
ELECTRIC CURRENT THROUGH GASES
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Objective 17videos
ELECTRIC CURRENT THROUGH GASES
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer17videos
ELECTRIC CURRENT IN CONDUCTORS
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 27videos
ELECTRIC FIELD AND POTENTIAL
Similar Questions
The conductivity of a pure semiconductor is roughly proportional to T32e−ΔE/2kT where (Δ)E is the band gap. The band gap for germanium is 0.74eV at 4K and 0.67eV at 300K.By what factor does the conductivity of pure germanium increase as the temperature is raised form 4K to 300K?
View SolutionHow will the saturation current in a diode with a caesium-coated tungsten cathode change, if the cathode temperature is raised from 1000 K to 1200 K?
View SolutionThe number of thermions emitted in a given time increases 100 times as the temperature of the emitting surface is increased from 600K→800K. Find the work function of the emitter. Boltzmann constant k=8.62×10−8eVk−1.
View Solution(a) Explain the following terms :
(i) Order of a reaction
(ii) Molecularity of a reaction
(b) The rate of a reaction increases four times when the temperature changes from 300 K to 320 K. Calculate the energy of activation of the reaction, assuming that it does not change with temperature. (R=8.314JK−1mol−1)View SolutionThe variation of pressure with volume of the gas at different temperatures can be graphically represented as shown in figure. On the basis of this graph answer the following question.
(i) How will the volume of a gas change if its pressure is increased at constant temperature ?
(ii) At a constant pressure, how will the volume of a gas change if the temperature is increased from 200 K to 400 K ?
 View Solution
View SolutionLight from a hydrogen tube is incident on the cathode of a photoelectric cell the work function of the cathode surface is 4.2eV. In order to reduce the photo - current to zero the voltage of the anode relative to the cathode must be made
View SolutionHalf life of a first order chemical reaction is 69 hr at 300 K. Also , rate of this reaction is doubled as temperature is increased from 300 K to 310 K. Determine activation energy and pre - exponential factor for this reaction.
View SolutionLet i0 be the thermionic current from a metal surface when the absolute temperature of the surface is T0. The temperature is slowly increased and the thermionic current is measured as a function of temperature. Which of the following plots may represent the variation in (ii0) against (TT0) ?
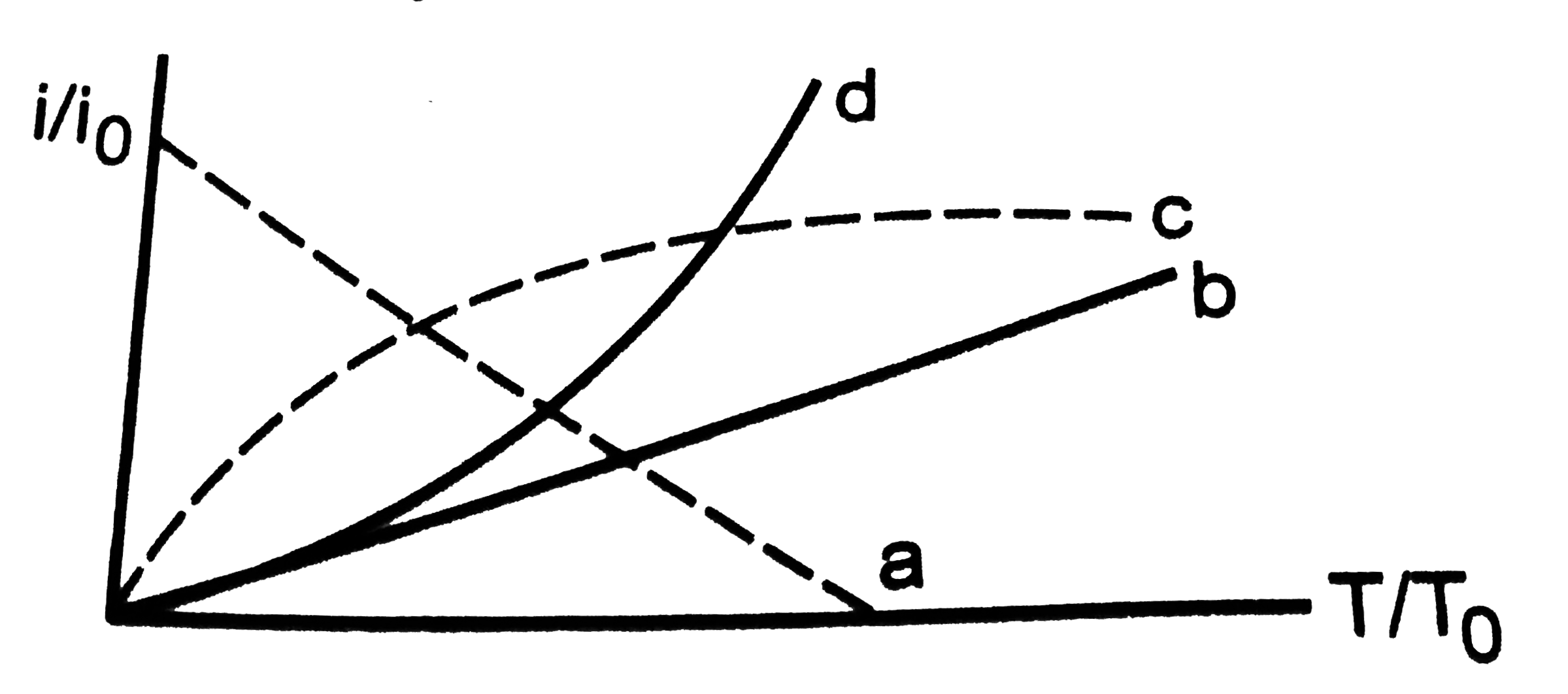 View Solution
View SolutionWhat is the activation energy (KJ/mol) for a reaction if its rate constant doubles when the temperature is raised from 300 K to 400 K ? (R=8.314 J mol−1K−1)
View SolutionWhat happens to the pressure of a sample of helium gas if the temperature is increased from 200 K to 800 K, with no change in volume?
View Solution

