The bohr radius is given by a0=ε0h2πme2 verify that the RHS has dimesions of length
The correct Answer is:A
To verify that the right-hand side (RHS) of the equation for the Bohr radius a0=ϵ0h2πme2 has dimensions of length, we will analyze the dimensions of each component in the equation step by step.
Step 1: Identify the components and their dimensions
1. Electric constant (ϵ0):
From Coulomb's law, we know that:
F=14πϵ0q1q2r2
Rearranging gives:
ϵ0=q2Fr2
The dimensions of charge q are (Q)=A⋅T (Ampere-second), so:
(q2)=(A2T2)
The dimensions of force F are (F)=MLT−2, and the dimensions of radius r are (L). Therefore:
(ϵ0)=(A2T2)(MLT−2)(L2)=(A2T2)(ML3T−2)=(A2T4)(ML3)
2. Planck's constant (h):
The dimensions of h (Planck's constant) are:
(h)=(E)(T)=(ML2T−2)(T)=(ML2T−1)
3. Mass (m):
The dimensions of mass m are simply:
(m)=(M)
4. Charge (e):
The dimensions of charge e are the same as q:
(e)=(AT)
Therefore:
(e2)=(A2T2)
Step 2: Substitute dimensions into the RHS
Now we substitute the dimensions into the RHS of the equation:
a0=ϵ0h2πme2
Ignoring the dimensionless constant π, we have:
(a0)=(ϵ0)(h)2(m)(e)2
Substituting the dimensions we found:
(a0)=(A2T4)(ML3)⋅((ML2T−1))2(M)⋅(A2T2)
Step 3: Simplifying the expression
Now we simplify the expression:
1. The numerator becomes:
(A2T4)(ML3)⋅(M2L4T−2)=(A2T4M2L4)(ML3)
This simplifies to:
(A2T4ML)(after canceling one M and one L from denominator)
2. The denominator is:
(M)⋅(A2T2)=(MA2T2)
Putting it all together:
(a0)=(A2T4ML)(MA2T2)=(L)⋅(T2)=(L)
Conclusion
Thus, we find that the dimensions of a0 indeed simplify to (L), confirming that the RHS has dimensions of length.
From Coulomb's law, we know that:
F=14πϵ0q1q2r2
Rearranging gives:
ϵ0=q2Fr2
The dimensions of charge q are (Q)=A⋅T (Ampere-second), so:
(q2)=(A2T2)
The dimensions of force F are (F)=MLT−2, and the dimensions of radius r are (L). Therefore:
(ϵ0)=(A2T2)(MLT−2)(L2)=(A2T2)(ML3T−2)=(A2T4)(ML3)
The dimensions of h (Planck's constant) are:
(h)=(E)(T)=(ML2T−2)(T)=(ML2T−1)
The dimensions of mass m are simply:
(m)=(M)
The dimensions of charge e are the same as q:
(e)=(AT)
Therefore:
(e2)=(A2T2)
a0=ϵ0h2πme2
(a0)=(ϵ0)(h)2(m)(e)2
(a0)=(A2T4)(ML3)⋅((ML2T−1))2(M)⋅(A2T2)
1. The numerator becomes:
(A2T4)(ML3)⋅(M2L4T−2)=(A2T4M2L4)(ML3)
This simplifies to:
(A2T4ML)(after canceling one M and one L from denominator)
(M)⋅(A2T2)=(MA2T2)
(a0)=(A2T4ML)(MA2T2)=(L)⋅(T2)=(L)
Topper's Solved these Questions
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Obejective - II
5 Videos
- ALTERNATING CURRENTBOOK - HC VERMA ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Short answer
14 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer
7 Videos
Similar Questions
Knowledge Check
The radius of the stationary state which is also called Bohr radius is given by the expression rn=n2a0 where the value of a0 is
A52.9 pmB5.29 pmC529 pmD0.529 pm
In the Bohr model of a π−mesic atom , a π−mesic of mass mπ and of the same charge as the electron is in a circular orbit of ratio of radius r about the nucleus with an orbital angular momentum h/2π. If the radius of a nucleus of atomic number Z is given by R=1.6×10−15Z13m, then the limit on Z for which (ε0h2/πme2=0.53Åandmπ/me=264)π−mesic atoms might exist is
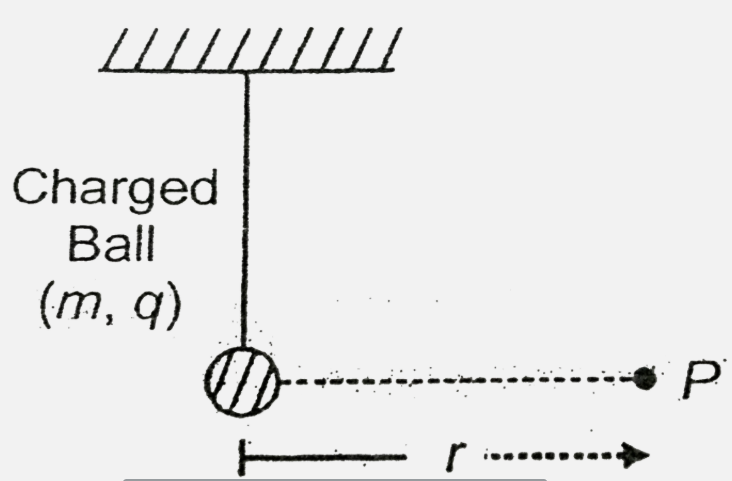
View SolutionThe electric field at point P due to a charged ball is given by
Ep=14πε0qr2
To measure 'E' at point P, A test charge q0 is placed at point P and measure electric force F upon the test charge. Check whether Fq0 is equal to 14πε0qr2 or not .
View SolutionThe parameter mQ4ε20h2 has the dimensions of ( m = mass Q = charge ∈0 = Permittivity and h = Planck's constant )
View SolutionThe maximum electric field upon the axis of a circular ring (q,R) is given by E=qπε0R2×16√n . Find n.
View SolutionThe dimension of e2/ε0hc (here symbols have their usual meanings) are
View SolutionThe dimension of (12)ε0E2 (ε0 : permittivity of free space, E electric field
View SolutionThe dimension of (12)ε0E2 (ε0 : permittivity of free space, E electric field
View Solution
