A,B and C are isodiaphers while C,D and E are isobars. Calculate the difference of protons between A and E .20682A→B→C→D→E
Given: Isodiaphers and isobars are formed in successive α and β−emission respectively.
The correct Answer is:2
To solve the problem, we need to understand the concepts of isodiaphers and isobars, and how they relate to alpha and beta emissions.
1. Identify Isodiaphers:
- Isodiaphers are nuclides that have the same value of N−Z (where N is the number of neutrons and Z is the number of protons).
- Given nuclides A, B, and C are isodiaphers.
2. Determine the Mass and Atomic Numbers of A, B, and C:
- Start with nuclide A, which is given as 20682A.
- This means A has:
- Mass number (A) = 206
- Atomic number (Z) = 82
- Neutrons (N) = Mass number - Atomic number = 206 - 82 = 124
3. Alpha Emission from A to B:
- In alpha emission, the mass number decreases by 4 and the atomic number decreases by 2.
- Therefore, for nuclide B:
- Mass number = 206 - 4 = 202
- Atomic number = 82 - 2 = 80
- So, B=20280B.
4. Alpha Emission from B to C:
- Again, applying alpha emission:
- For nuclide C:
- Mass number = 202 - 4 = 198
- Atomic number = 80 - 2 = 78
- So, C=19878C.
5. Identify Isobars:
- Isobars are nuclides that have the same mass number but different atomic numbers.
- Given nuclides C, D, and E are isobars.
6. Beta Emission from C to D:
- In beta emission, the mass number remains the same, but the atomic number increases by 1.
- Therefore, for nuclide D:
- Mass number = 198 (remains the same)
- Atomic number = 78 + 1 = 79
- So, D=19879D.
7. Beta Emission from D to E:
- Again, applying beta emission:
- For nuclide E:
- Mass number = 198 (remains the same)
- Atomic number = 79 + 1 = 80
- So, E=19880E.
8. Calculate the Difference in Protons between A and E:
- The atomic number of A is 82 (which is the number of protons).
- The atomic number of E is 80 (which is the number of protons).
- The difference in the number of protons between A and E is:
Difference=ZA−ZE=82−80=2
Final Answer:
The difference in the number of protons between A and E is 2.
- Isodiaphers are nuclides that have the same value of N−Z (where N is the number of neutrons and Z is the number of protons).
- Given nuclides A, B, and C are isodiaphers.
- Start with nuclide A, which is given as 20682A.
- This means A has:
- Mass number (A) = 206
- Atomic number (Z) = 82
- Neutrons (N) = Mass number - Atomic number = 206 - 82 = 124
- In alpha emission, the mass number decreases by 4 and the atomic number decreases by 2.
- Therefore, for nuclide B:
- Mass number = 206 - 4 = 202
- Atomic number = 82 - 2 = 80
- So, B=20280B.
- Again, applying alpha emission:
- For nuclide C:
- Mass number = 202 - 4 = 198
- Atomic number = 80 - 2 = 78
- So, C=19878C.
- Isobars are nuclides that have the same mass number but different atomic numbers.
- Given nuclides C, D, and E are isobars.
- In beta emission, the mass number remains the same, but the atomic number increases by 1.
- Therefore, for nuclide D:
- Mass number = 198 (remains the same)
- Atomic number = 78 + 1 = 79
- So, D=19879D.
- Again, applying beta emission:
- For nuclide E:
- Mass number = 198 (remains the same)
- Atomic number = 79 + 1 = 80
- So, E=19880E.
- The atomic number of A is 82 (which is the number of protons).
- The atomic number of E is 80 (which is the number of protons).
- The difference in the number of protons between A and E is:
Difference=ZA−ZE=82−80=2
The difference in the number of protons between A and E is 2.
Similar Questions
Identify A,B,C,D and E in given diagram:
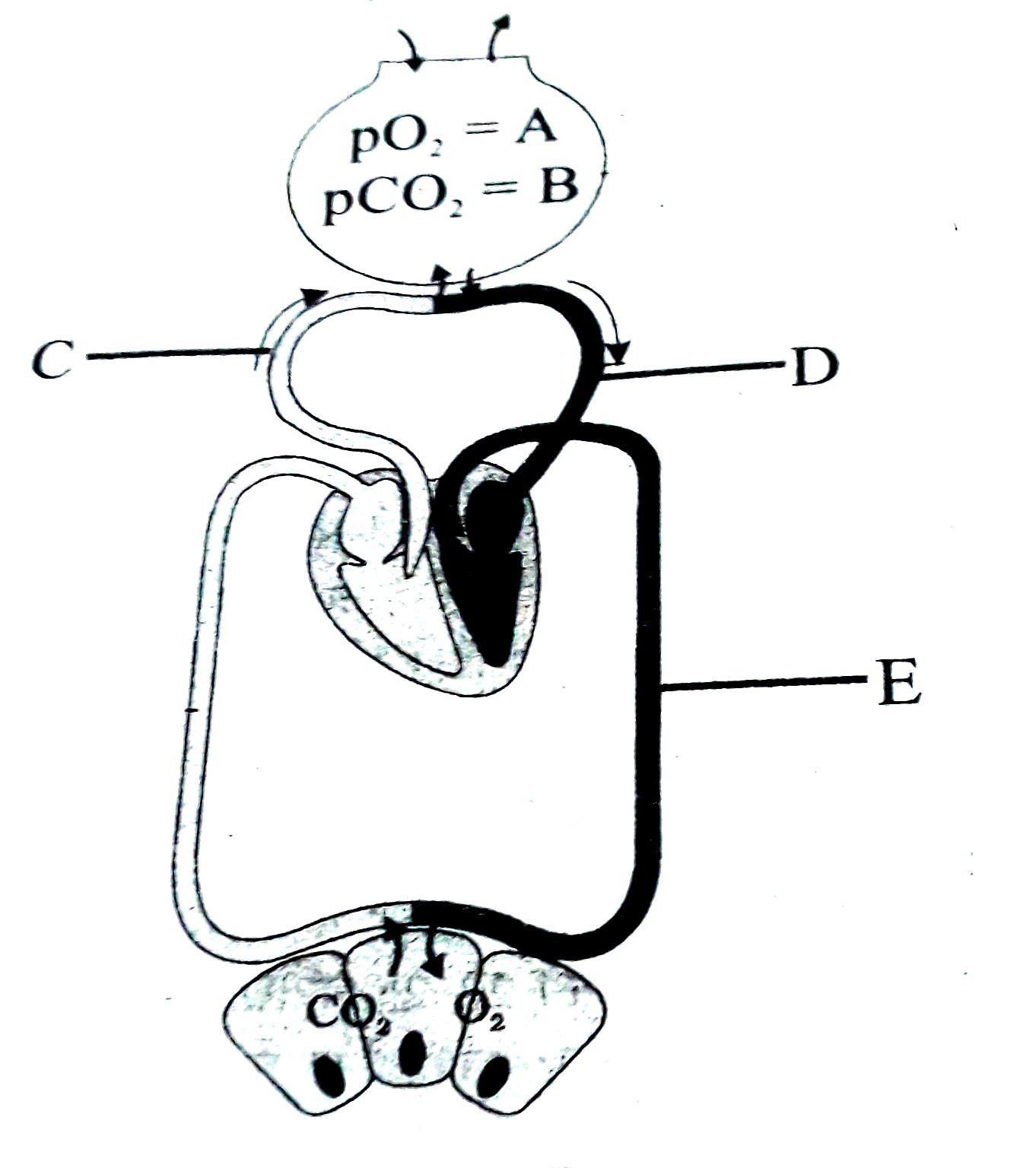
View SolutionIf a,b,c,d,e, f are A. M's between 2 and 12 , then find a+b+c+d+e+f.
View SolutionIn ABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ADE and ABC .
View SolutionD and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD=AE . Prove that B,C,D,E are concylic.
View SolutionIn Figure, chord ED is parallel to the diameter AC of the circle. Given ∠CBE=65∘, calculate ∠DEC.
View SolutionIn a ABC, BD and CE are the altitudes. Prove that ADB and AEC are similar. Is CDB~BEC ?
View SolutionAD and BE are respectively altitudes of an isosceles triangle ABC with AC=BC . Prove that AE=BD.
View SolutionIn Figure, AD and BE are respectively altitudes of an isosceles triangle ABC with AC=BC. Prove that AE=BD
View SolutionD and E are points on the sides AB and AC respectively of a ABC such that DEBC and divides ABC into two parts, equal in area, find BDAB .
View SolutionIf a,b,c, are in A.P., b,c,d are in G.P. and c,d,e, are in H.P., then a,c,e are in
View Solution
