In NaCl the centres of two nearst like-charged ions are present at a distance of:
12a√2
12a
√32a
1√22a
The correct Answer is:A
To solve the question regarding the distance between the centers of two nearest like-charged ions in NaCl, we can follow these steps:
1. Understanding the Structure of NaCl:
- Sodium chloride (NaCl) crystallizes in a face-centered cubic (FCC) lattice structure. In this structure, chloride ions (Cl⁻) are located at the corners and the face centers of the cube.
2. Identifying the Positions of Ions:
- In the FCC lattice, there are 8 corner ions and 6 face-centered ions. The sodium ions (Na⁺) occupy the octahedral voids formed by the chloride ions.
3. Determining the Edge Length:
- Let the edge length of the unit cell be denoted as 'a'. The ions in the FCC structure touch each other along the face diagonal.
4. Calculating the Face Diagonal:
- The face diagonal (d) of the cube can be calculated using the Pythagorean theorem:
d=√a2+a2=√2a2=a√2
5. Understanding Ion Touching:
- In the NaCl structure, the chloride ions touch each other along the face diagonal. The distance between the centers of two nearest like-charged ions (Cl⁻ ions) will be equal to the face diagonal.
6. Relating Ion Radius to Edge Length:
- Since the face diagonal is made up of the radii of two chloride ions and the distance between them, we can express this as:
d=4r
- Here, 'r' is the radius of the chloride ion. Therefore, we have:
a√2=4r
7. Finding the Radius:
- From the equation above, we can solve for 'r':
r=a√24=a2√2
8. Calculating the Distance Between Nearest Like-Charged Ions:
- The distance between the centers of two nearest like-charged ions (Cl⁻ ions) is given by:
Distance=2r=2×a2√2=a√2
9. Final Answer:
- Therefore, the centers of two nearest like-charged ions in NaCl are present at a distance of:
a√2
- Sodium chloride (NaCl) crystallizes in a face-centered cubic (FCC) lattice structure. In this structure, chloride ions (Cl⁻) are located at the corners and the face centers of the cube.
- In the FCC lattice, there are 8 corner ions and 6 face-centered ions. The sodium ions (Na⁺) occupy the octahedral voids formed by the chloride ions.
- Let the edge length of the unit cell be denoted as 'a'. The ions in the FCC structure touch each other along the face diagonal.
- The face diagonal (d) of the cube can be calculated using the Pythagorean theorem:
d=√a2+a2=√2a2=a√2
- In the NaCl structure, the chloride ions touch each other along the face diagonal. The distance between the centers of two nearest like-charged ions (Cl⁻ ions) will be equal to the face diagonal.
- Since the face diagonal is made up of the radii of two chloride ions and the distance between them, we can express this as:
d=4r
- Here, 'r' is the radius of the chloride ion. Therefore, we have:
a√2=4r
- From the equation above, we can solve for 'r':
r=a√24=a2√2
- The distance between the centers of two nearest like-charged ions (Cl⁻ ions) is given by:
Distance=2r=2×a2√2=a√2
- Therefore, the centers of two nearest like-charged ions in NaCl are present at a distance of:
a√2
Topper's Solved these Questions
- SOLID STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - SOLID STATEEXERCISE - Level-2
32 Videos
- SOLID STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - SOLID STATEEXERCISE - Level 3 passage -1
1 Videos
- IONIC EEQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - IONIC EEQUILIBRIUMEXERCISE - Subjective problems
1 Videos
- STOICHIOMETRYBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Match the Colum-II
6 Videos
Similar Questions
Kinetin like properties are present in
View SolutionPeroxide ion is present in :
View SolutionTwo spheres A and B are charged with the charges of +10 and +20 coulomb respectively and separated by a distance of 80 cm. The electric field at point on the line joining the centres of the two spheres will be zero at a distance from the sphere A :
View SolutionThe force of repulsion between two point charges is F, when these are at a distance of 1m. Now the point charges are replaced by spheres of radii 25cm having the charge same as that of point charges. The distance between their centres is 1m, then compare the force of repulsion in two cases.
View SolutionA sphere of radius R carries charge such that its volume charge density is proportional to the square of the distance from the centre. What is the ratio of the magnitude of the electric field at a distance 2 R from the centre to the magnitude of the electric field at a distance of R/2 from the centre?
View SolutionA charge 'q' is placed at the centre of a conducting spherical shell of radius R, which is given a charge Q. An external charge Q' is also present at distance R'(R'>R) from 'q'. Then the resultant field will be best represented for region r<R by : [where r is the distance of the point from q]
View SolutionThe force of repulsion between two point charges is F, when these are at distance 0.5m apart. Now the point charges are replaced by spheres of radii 5 cm each having the same charge as that of the respective point charge. The distance between their centres is again kept 0.5 m. Then the force of repulsion will
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R/2 from the centre of the shell is
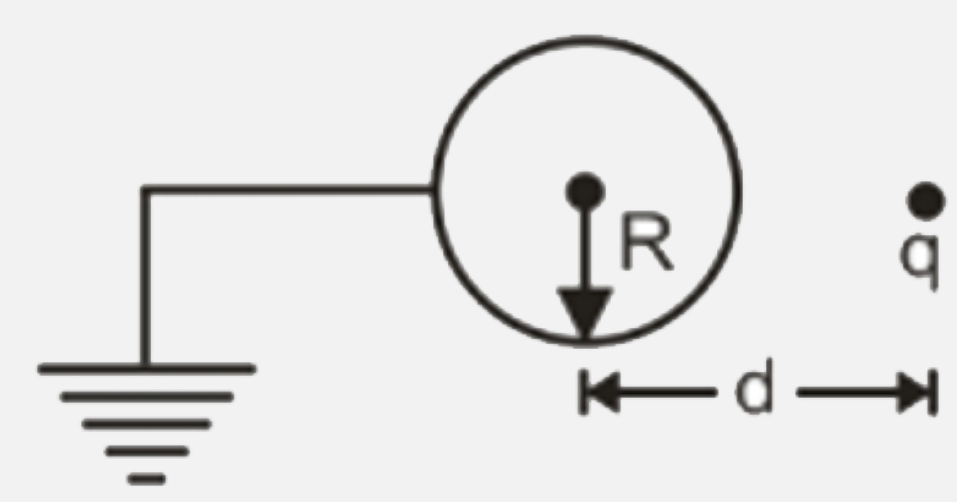
View SolutionIn the shown figure, the charge appearing on the conducting shell (grounded) of Radius R, when a point charge q is kept at a distance of d from the centre of the sphere is:
View Solution
