A sphere of radius R carries charge such that its volume charge density is proportional to the square of the distance from the centre. What is the ratio of the magnitude of the electric field at a distance 2 R from the centre to the magnitude of the electric field at a distance of R/2 from the centre?
1
2
4
8
The correct Answer is:B
To solve the problem step by step, we will follow the logic presented in the video transcript, while ensuring clarity in each step.
Step 1: Understand the Charge Density
The volume charge density ρ is given to be proportional to the square of the distance from the center of the sphere. We can express this as:
ρ=kr2
where k is a constant and r is the distance from the center.
Step 2: Calculate the Charge Enclosed
To find the electric field using Gauss's law, we need to calculate the charge enclosed within a radius r. The charge enclosed Qenclosed can be calculated using the integral:
Qenclosed=∫r0ρdV
where dV=4πr′2dr′. Substituting ρ:
Qenclosed=∫r0k(r′)2(4π(r′)2)dr′=4πk∫r0(r′)4dr′
Calculating the integral:
∫r0(r′)4dr′=r55
Thus,
Qenclosed=4πk⋅r55=4πkr55
Step 3: Apply Gauss's Law
According to Gauss's law, the electric field E at a distance r from the center is given by:
∮E⋅dS=Qenclosedϵ0
For a spherical surface of radius r:
E⋅4πr2=4πkr55ϵ0
Thus,
E=kr35ϵ0
Step 4: Electric Field Outside the Sphere
For distances greater than the radius R of the sphere, the charge enclosed becomes constant:
Qenclosed=4πkR55
Using Gauss's law again:
E⋅4πr2=4πkR55ϵ0
Thus,
E=kR55ϵ0r2
Step 5: Calculate Electric Field at Specific Distances
1. At r=R2:
E(R2)=kR55ϵ0(R2)2=kR55ϵ0⋅R24=4kR35ϵ0
2. At r=2R:
E(2R)=kR55ϵ0(2R)2=kR55ϵ0⋅4R2=kR320ϵ0
Step 6: Find the Ratio of Electric Fields
Now, we need to find the ratio:
Ratio=E(2R)E(R2)=kR320ϵ04kR35ϵ0=120⋅54=580=116
Final Result
The ratio of the magnitude of the electric field at a distance 2R from the center to the magnitude of the electric field at a distance R2 from the center is:
116
The volume charge density ρ is given to be proportional to the square of the distance from the center of the sphere. We can express this as:
ρ=kr2
where k is a constant and r is the distance from the center.
To find the electric field using Gauss's law, we need to calculate the charge enclosed within a radius r. The charge enclosed Qenclosed can be calculated using the integral:
Qenclosed=∫r0ρdV
where dV=4πr′2dr′. Substituting ρ:
Qenclosed=∫r0k(r′)2(4π(r′)2)dr′=4πk∫r0(r′)4dr′
Calculating the integral:
∫r0(r′)4dr′=r55
Thus,
Qenclosed=4πk⋅r55=4πkr55
According to Gauss's law, the electric field E at a distance r from the center is given by:
∮E⋅dS=Qenclosedϵ0
For a spherical surface of radius r:
E⋅4πr2=4πkr55ϵ0
Thus,
E=kr35ϵ0
For distances greater than the radius R of the sphere, the charge enclosed becomes constant:
Qenclosed=4πkR55
Using Gauss's law again:
E⋅4πr2=4πkR55ϵ0
Thus,
E=kR55ϵ0r2
1. At r=R2:
E(R2)=kR55ϵ0(R2)2=kR55ϵ0⋅R24=4kR35ϵ0
E(2R)=kR55ϵ0(2R)2=kR55ϵ0⋅4R2=kR320ϵ0
Now, we need to find the ratio:
Ratio=E(2R)E(R2)=kR320ϵ04kR35ϵ0=120⋅54=580=116
The ratio of the magnitude of the electric field at a distance 2R from the center to the magnitude of the electric field at a distance R2 from the center is:
116
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct
8 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Comprehension
36 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective
12 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
Similar Questions
The field due to a magnet at a distance R~ from the centre of the magnet is proportional
View SolutionA solid non-conduction cylinder of radius R is charge such that volume charge density is proporation to r where r is distance from axis. The electric field E at a distance r(r<R) well depend on r as.
View Solution
Knowledge Check
The correct plot of the magnitude of magnetic field →B vs distance r from centre of the wire is, if the radius of wire is R
A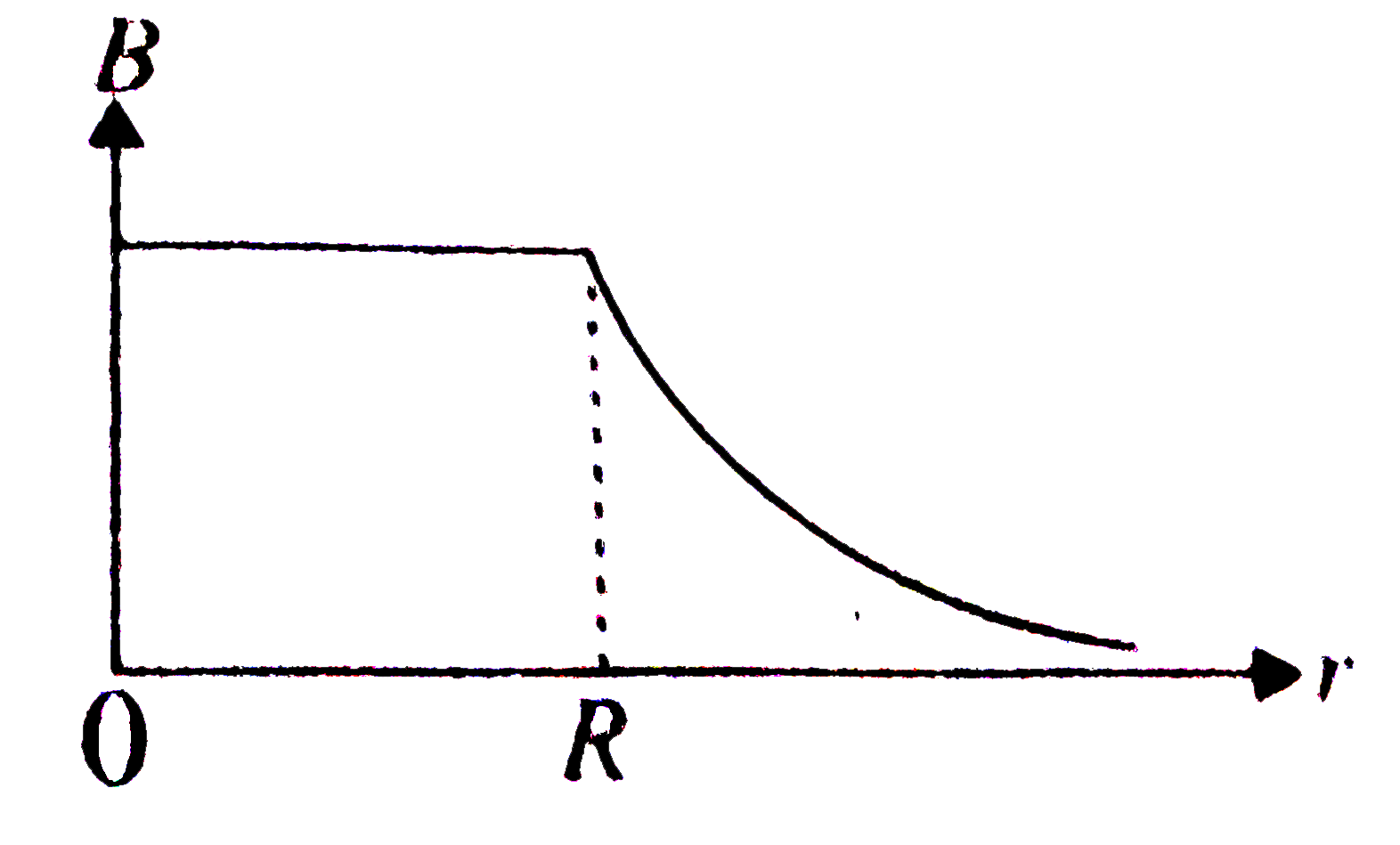 B
B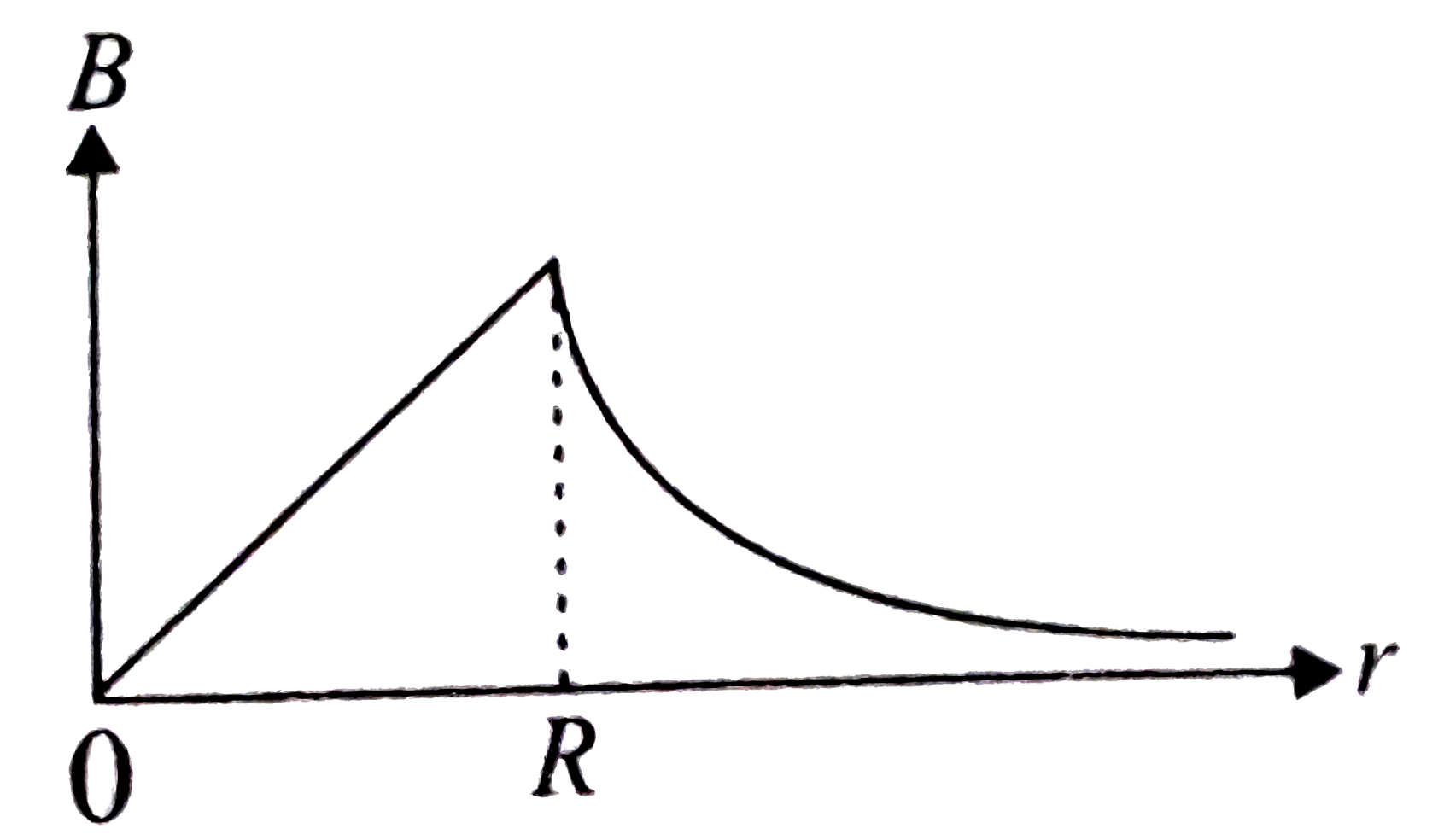 C
C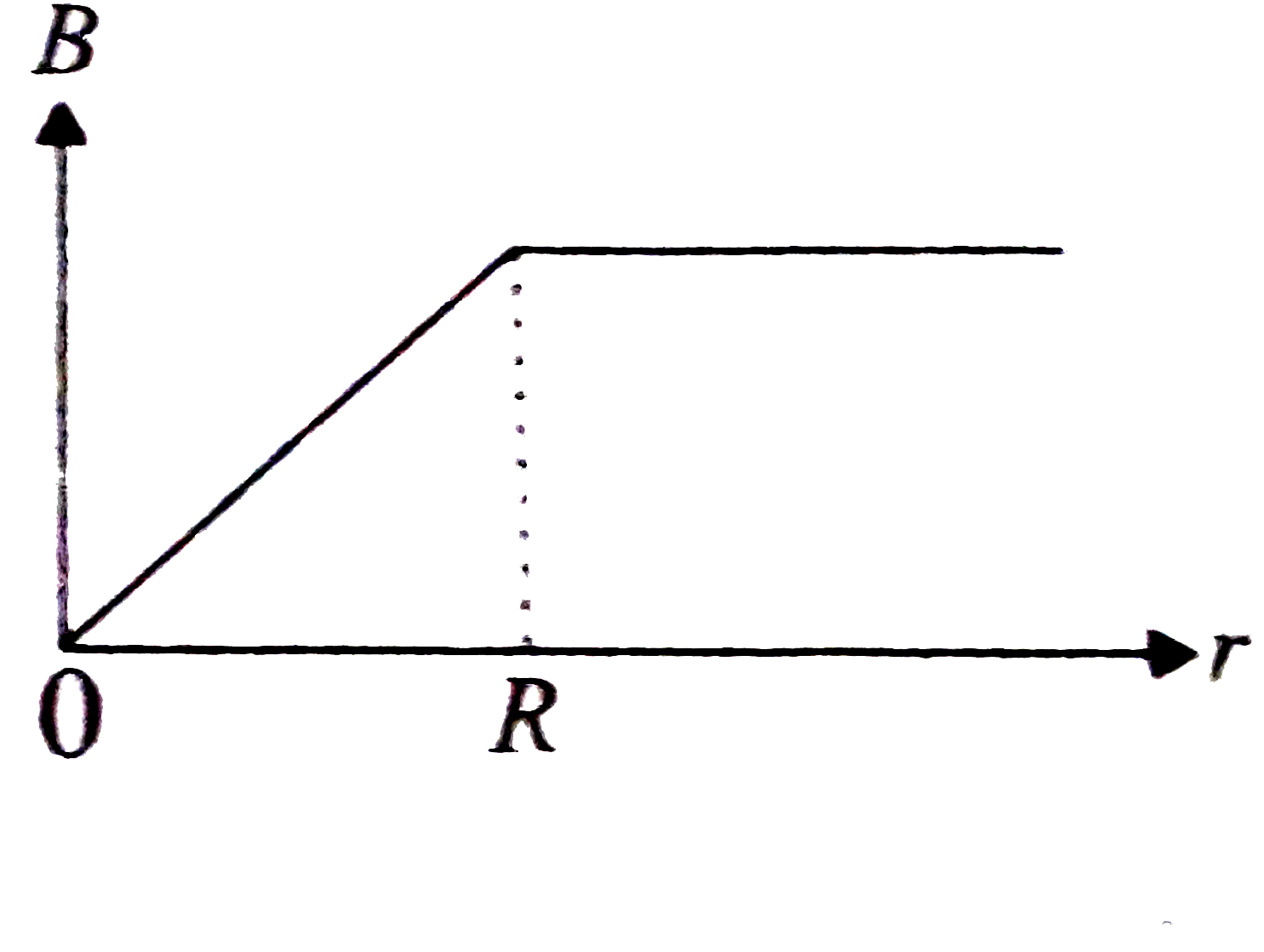 D
D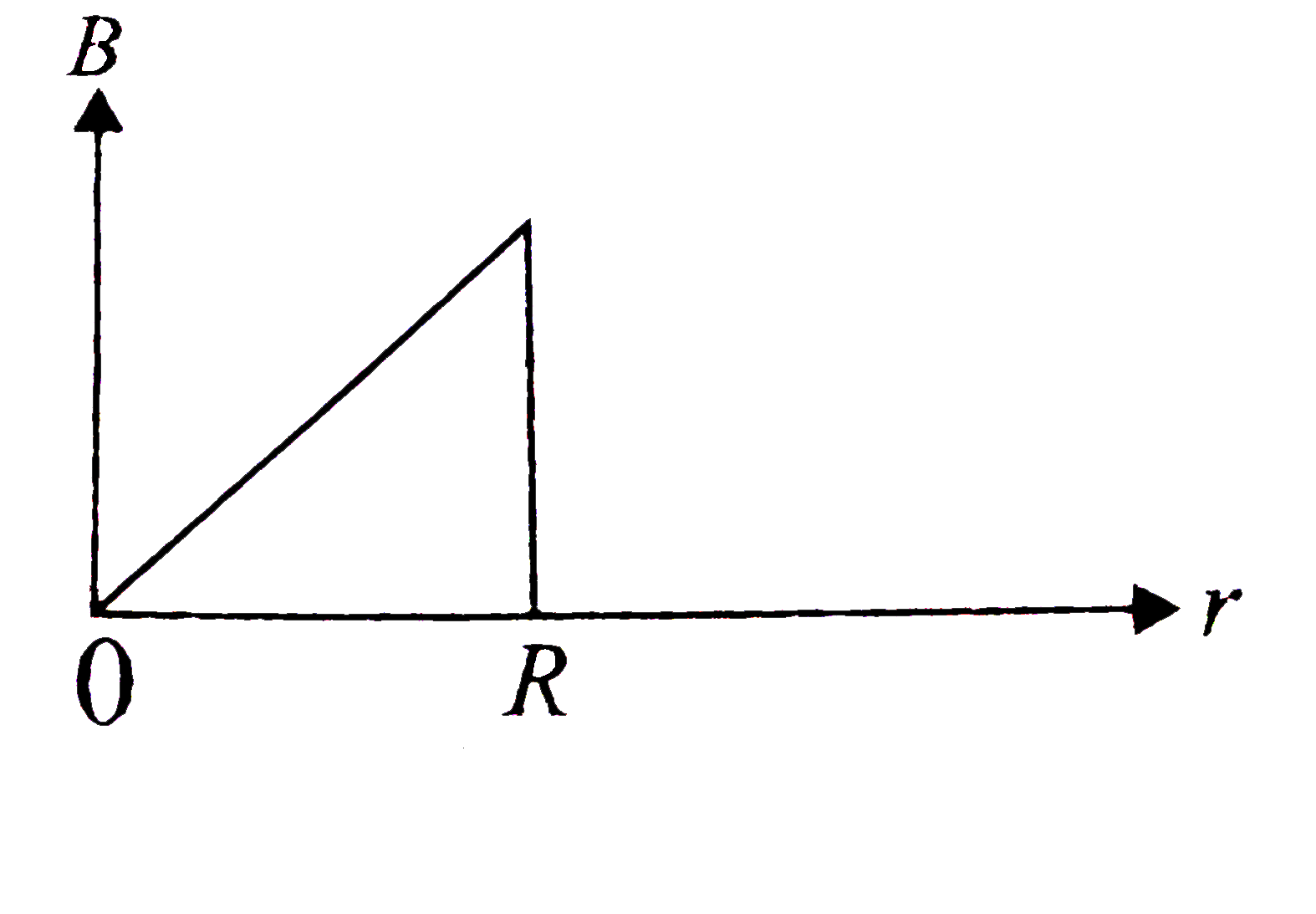
The gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View SolutionA point charge Q is placed at the centre of a spherical conducting shell. A total charge of -q is placed on the shell. The magnitude of the electric field at point P1 at a distance R1 from the centre is X. The magnitude of the electric field due to induced charges at point P2 a distance R2 from the centre is Y. The values of X and Y are respectively.

View SolutionA long thin flat sheet has a uniform surface charge density σ. The magnitude of the electric field at a distance .r. from it is given by
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionThe electric field at 2R from the centre of a uniformly charged non - conducting sphere of rarius R is E. The electric field at a distance R2 from the centre will be
View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View Solution
