For any H like system, the ratio of velocities of electron in I, II & III orbit i.e.,V1:V2:V3 will be:
(a) 1:2:3
(b) 1:12:13
(c) 3:2:1
(d) 1:1:1
The correct Answer is:B
To find the ratio of the velocities of the electron in the first, second, and third orbits (V1:V2:V3) for any hydrogen-like system, we can follow these steps:
1. Understanding the Relationship:
The velocity of an electron in a hydrogen-like atom is given by the formula:
Vn∝Zn
where Vn is the velocity in the nth orbit, Z is the atomic number, and n is the principal quantum number (the orbit number).
2. Identifying the Atomic Number:
For hydrogen-like systems, the atomic number Z is constant for a given atom. Therefore, we can focus on the relationship between the velocities and the orbit numbers.
3. Setting Up the Ratios:
Since Vn∝Zn, we can express the velocities for the first, second, and third orbits as:
V1∝Z1,V2∝Z2,V3∝Z3
4. Forming the Velocity Ratio:
The ratio of the velocities V1:V2:V3 can be expressed as:
V1:V2:V3=Z1:Z2:Z3
Since Z is common in all terms, it cancels out:
V1:V2:V3=1:12:13
5. Finding a Common Denominator:
To simplify this ratio, we can convert it to a common denominator:
1:12:13=6:3:2
6. Final Ratio:
Thus, the final ratio of velocities of the electron in the first, second, and third orbits is:
V1:V2:V3=6:3:2
Conclusion:
The ratio of the velocities of the electron in the first, second, and third orbits of a hydrogen-like system is 6:3:2.
The velocity of an electron in a hydrogen-like atom is given by the formula:
Vn∝Zn
where Vn is the velocity in the nth orbit, Z is the atomic number, and n is the principal quantum number (the orbit number).
For hydrogen-like systems, the atomic number Z is constant for a given atom. Therefore, we can focus on the relationship between the velocities and the orbit numbers.
Since Vn∝Zn, we can express the velocities for the first, second, and third orbits as:
V1∝Z1,V2∝Z2,V3∝Z3
The ratio of the velocities V1:V2:V3 can be expressed as:
V1:V2:V3=Z1:Z2:Z3
Since Z is common in all terms, it cancels out:
V1:V2:V3=1:12:13
To simplify this ratio, we can convert it to a common denominator:
1:12:13=6:3:2
Thus, the final ratio of velocities of the electron in the first, second, and third orbits is:
V1:V2:V3=6:3:2
The ratio of the velocities of the electron in the first, second, and third orbits of a hydrogen-like system is 6:3:2.
Topper's Solved these Questions
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - level 2
30 Videos
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - Level 3 (Passage 1)
3 Videos
- CHEMICAL EQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Match the column
1 Videos
Similar Questions
Knowledge Check
velocity of sound is measured in hydrogen and oxygen gases at a given temperature. The ratio of two velocities will be (VH/V0)
A1:4B4:1C1:1D32:1
If the radius of an orbit is r and the velocity of electron in it is v , then the frequency of electron in the orbit will be
View SolutionThe velocity of an electron in the first orbit of H atom is v. The velocity of an electron in the 2nd orbit of He+ atom.
View SolutionPotential difference across AB , i.e., VA−VB is

View SolutionPotential difference between points A and B (i.e. VA−VB) is -----
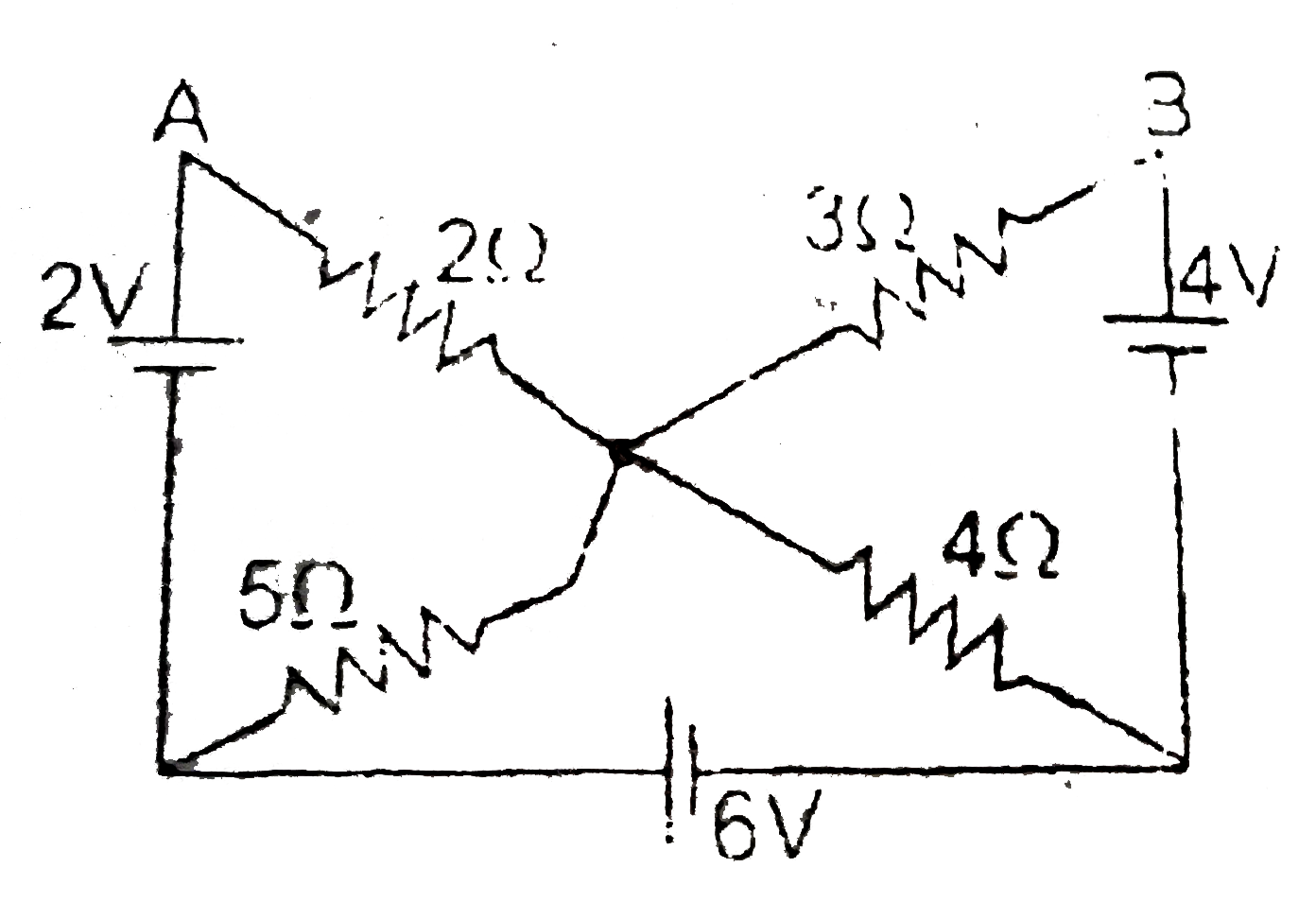
View SolutionFind the equivalent resistance of the network shown in the figure between the points A and B if
(i) VA>VB (ii) VA<VB

View SolutionThe orbital velocity of electron in the ground state is v. If the electron is excited to enegry staet −0.54eV its orbital velocity will be
View SolutionA plenet moving along an elliptical orbit is closest to the sun at a distance r1 and farthest away at a distance of r2. If v1 and v2 are the linear velocities at these points respectively, then the ratio v1v2 is
View Solution
