The ratio of slopes of Kmax vs. V and V0 vs. v curves in the photoelectric effect gives (v= freqency. Kmax= maximum kinetic energy, V0=stopping potential) :
charge of electron
Planck's constant
work function
the ratio of Planck's constant and electronic charge
The correct Answer is:A
To solve the question regarding the ratio of slopes of the Kmax vs. ν and V0 vs. ν curves in the photoelectric effect, we will follow these steps:
Step 1: Understand the Photoelectric Effect
The photoelectric effect is described by Einstein's photoelectric equation:
hν=Φ+Kmax
where:
- h is Planck's constant,
- ν is the frequency of the incident light,
- Φ is the work function of the material,
- Kmax is the maximum kinetic energy of the emitted electrons.
Step 2: Derive the Equation for Kmax
Rearranging the photoelectric equation gives:
Kmax=hν−Φ
This equation shows that Kmax is a linear function of ν with a slope of h.
Step 3: Plot the Graph for Kmax vs. ν
When we plot Kmax on the y-axis and ν on the x-axis, the graph will be a straight line:
Kmax=hν−Φ
The slope of this line (let's denote it as m1) is:
m1=h
Step 4: Understand the Stopping Potential
The stopping potential V0 is related to the maximum kinetic energy by:
Kmax=eV0
where e is the charge of the electron.
Step 5: Derive the Equation for V0
From the photoelectric equation, we can also express it as:
hν=hν0+eV0
Rearranging gives:
V0=hνe−hν0e
This shows that V0 is also a linear function of ν.
Step 6: Plot the Graph for V0 vs. ν
When we plot V0 on the y-axis and ν on the x-axis, the graph will be:
V0=heν−hν0e
The slope of this line (let's denote it as m2) is:
m2=he
Step 7: Calculate the Ratio of Slopes
Now, we find the ratio of the slopes:
Ratio=m1m2=hhe=e
Conclusion
The ratio of the slopes of the Kmax vs. ν curve and the V0 vs. ν curve is equal to the charge of the electron e.
Final Answer
The ratio of slopes is e (the charge of the electron).
---
The photoelectric effect is described by Einstein's photoelectric equation:
hν=Φ+Kmax
where:
- h is Planck's constant,
- ν is the frequency of the incident light,
- Φ is the work function of the material,
- Kmax is the maximum kinetic energy of the emitted electrons.
Rearranging the photoelectric equation gives:
Kmax=hν−Φ
This equation shows that Kmax is a linear function of ν with a slope of h.
When we plot Kmax on the y-axis and ν on the x-axis, the graph will be a straight line:
Kmax=hν−Φ
The slope of this line (let's denote it as m1) is:
m1=h
The stopping potential V0 is related to the maximum kinetic energy by:
Kmax=eV0
where e is the charge of the electron.
From the photoelectric equation, we can also express it as:
hν=hν0+eV0
Rearranging gives:
V0=hνe−hν0e
This shows that V0 is also a linear function of ν.
When we plot V0 on the y-axis and ν on the x-axis, the graph will be:
V0=heν−hν0e
The slope of this line (let's denote it as m2) is:
m2=he
Now, we find the ratio of the slopes:
Ratio=m1m2=hhe=e
The ratio of the slopes of the Kmax vs. ν curve and the V0 vs. ν curve is equal to the charge of the electron e.
The ratio of slopes is e (the charge of the electron).
Topper's Solved these Questions
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - level 2
30 Videos
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - Level 3 (Passage 1)
3 Videos
- CHEMICAL EQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Match the column
1 Videos
Similar Questions
Slope of V0 vs v curve is (where V0= Stopping potential, v=subjected freqency)
View SolutionThis question has statement - 1 and statement - 2 of the four choice given after the statements choose the one that best describes the two statements
statement - 1 : A metallic surface is irradiated by a monochromatic light of frequency v>v0 (the threshold frequency). The maximum kinetic energy and the stopping potential are KmaxandV0 respectively if the frequency incident on the surface is doubled , both the KmaxandV0 are also doubled
statement - 2 : The maximum kinetic energy and the stopping potential of photoelectron emitted from a surface are linearly dependent on the frequency of incident light
View SolutionThe emission of electrons from a metal surface exposed rto light radaition of appropriate wavelength is called photoelectric effect .The emmited electron are called photo=-weklectron work function of threshold energy may be defined as the minimum amount of energy required to ejected electron from a most surface .According to Einstein
Maximum kinetic energy of ejected electron = Absorbed energy - Work function
12mv2max=h(v)−h(vn)=hv[1λ−1λn]
Where vn and λ0 are thereshold frequency and threshold wavelength respectively
Sopping potential : it is the miximum potential at which the photoelectric current becomes zero if V0 is the stopping potential eV0=h(v−v0)
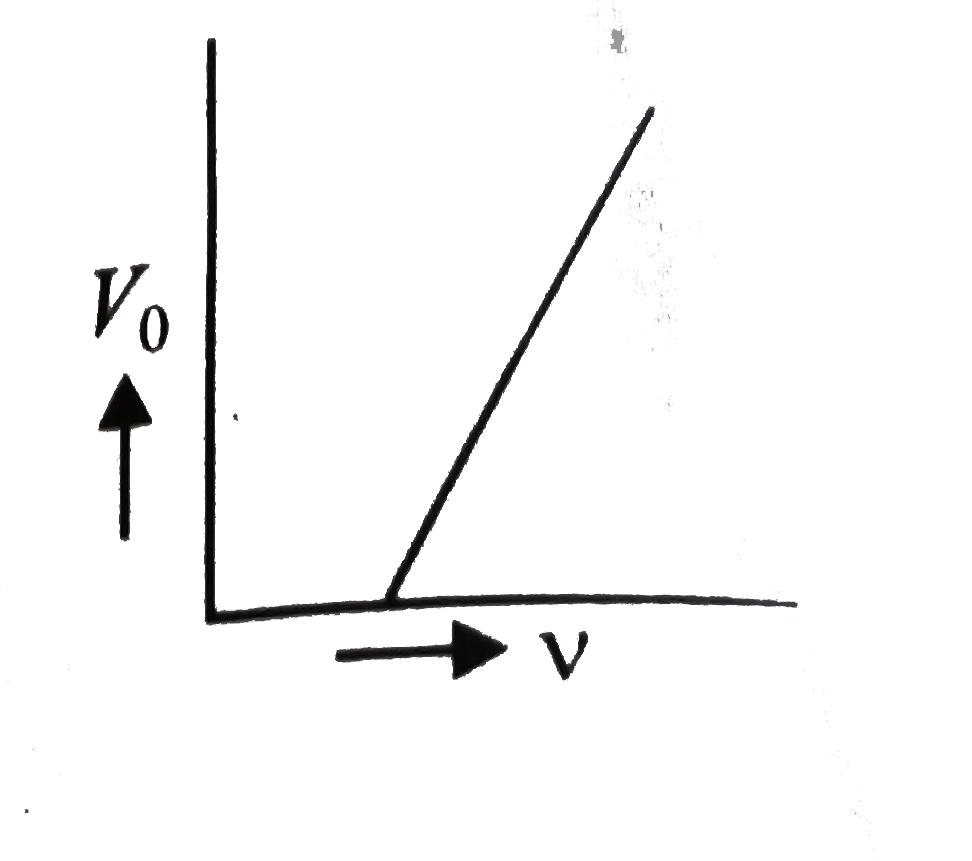
In the photoelectric currect effect the shape of strainght line graph between stopping potential (V0) and frequency of incident light (V) gves
View SolutionThe stopping potential in an experiment on photoelectric effect is 2V. What is the maximum kinetic energy of the photoelectrons emitted ?
View SolutionThe stopping potential in an experiment on a photo electric effect is 1.5 V. What is the maximum kinetic energy of the photoelectrons emitted?
View SolutionThe emission of electrons from a metal surface exposed rto light radaition of appropriate wavelength is called photoelectroic effect .The emmited electron are called photo=-weklectron work function of threshold energy may be defined as the minimum amount of energy required to ejercted electron from a most surface .According to Einstein
Maximum kinetic energy of ejected electron = Aborbed energy - Work function
12mv2max=h(v)−h(vn)=hv[1λ−01λn]
Where vn and λ0 are thereshold frequency and threshold wavelength respectively
Sopping potential : it is the miximum potential at which the photoelectric current becomes zero if V0 is the stopping potential eV0=h(v−v0)
Whaich of the following is the graph between the frequency (V) of the incident radiation and the stopping potential (v) ?
View SolutionWhen a monochromatic point source of light is at a distance
of 0.2 m from a photoelectric cell, the cut off voltage and the saturation current
are respectively 0.6 V and 18.0 mA. If the same source is placed 0.6 m away
from the photoelectric cell, then
(a) the stopping potential will be 0.2 V
(b) the stopping potential will be 0.6 V
(c ) the saturation current will be 6.0 mA
(d) the saturation current will be 2.0 mA
View SolutionThe emission of electrons from a metal surface exposed rto light radaition of appropriate wavelength is called photoelectroic effect .The emmited electron are called photo=-weklectron work function of threshold energy may be defined as the minimum amount of energy required to ejercted electron from a most surface .According to Einstein
Maximum kinetic energy of ejected electron = Aborbed energy - Work function
12mv2max=h(v)−h(vn)=hv[1λ−01λn]
Where vn and λ0 are thereshold frequency and threshold wavelength respectively
Sopping potential : it is the miximum potential at which the photoelectric current becomes zero if V0 is the stopping potential eV0=h(v−v0)
The stopping potential as a function on electron frtequency is plotted for two photoelectric surface A abd B The graph show that the work function of A is

View SolutionWhen a metallic surface is illuminated by a monochromatic light of λ the stopping potential for photoelectric current is 4V0 when the same surface is illuminated by light of wavelength 3λ the stopping potential isV0The threshold wavelength for this surface for photoelectric effect is -
View SolutionIf the threshold frequency of a metal for photoelectric effect is v0 then which of the following will not happen ?
View Solution
