Slope of V0 vs v curve is (where V0= Stopping potential, v=subjected freqency)
e
he
ϕ
h
The correct Answer is:B
To find the slope of the V0 versus ν curve, where V0 is the stopping potential and ν is the subjected frequency, we can follow these steps:
1. Understand the Photoelectric Effect:
When light of frequency ν strikes a metal surface, it can eject electrons if the energy of the light (given by hν, where h is Planck's constant) is greater than the work function ϕ (denoted as hν0) of the metal.
2. Energy Equation:
The energy of the incident photons can be expressed as:
hν=ϕ+KE
where KE is the kinetic energy of the emitted electrons.
3. Relate Kinetic Energy to Stopping Potential:
The kinetic energy of the emitted electrons can also be expressed in terms of the stopping potential V0:
KE=eV0
where e is the charge of the electron.
4. Combine the Equations:
By substituting KE into the energy equation, we get:
hν=hν0+eV0
5. Rearranging the Equation:
Rearranging the equation to express V0 in terms of ν:
eV0=hν−hν0
Dividing through by e:
V0=heν−hν0e
6. Identify the Linear Relationship:
The equation V0=heν−hν0e is in the form of y=mx+c, where:
- y=V0
- x=ν
- m=he (the slope)
- c=−hν0e (the y-intercept)
7. Conclusion:
Therefore, the slope of the V0 versus ν curve is:
slope=he
Final Answer:
The slope of the V0 versus ν curve is he.
---
When light of frequency ν strikes a metal surface, it can eject electrons if the energy of the light (given by hν, where h is Planck's constant) is greater than the work function ϕ (denoted as hν0) of the metal.
The energy of the incident photons can be expressed as:
hν=ϕ+KE
where KE is the kinetic energy of the emitted electrons.
The kinetic energy of the emitted electrons can also be expressed in terms of the stopping potential V0:
KE=eV0
where e is the charge of the electron.
By substituting KE into the energy equation, we get:
hν=hν0+eV0
Rearranging the equation to express V0 in terms of ν:
eV0=hν−hν0
Dividing through by e:
V0=heν−hν0e
The equation V0=heν−hν0e is in the form of y=mx+c, where:
- y=V0
- x=ν
- m=he (the slope)
- c=−hν0e (the y-intercept)
Therefore, the slope of the V0 versus ν curve is:
slope=he
The slope of the V0 versus ν curve is he.
Topper's Solved these Questions
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - level 2
30 Videos
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - Level 3 (Passage 1)
3 Videos
- CHEMICAL EQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Match the column
1 Videos
Similar Questions
(i) Plot a labelled graph of |Vs| where Vs is stopping potential versus frequency f of the incident radiation.
(ii) State how will you use this graph to determine the value of Planck.s constant.
View Solution(i) Plot a labelled graph of |Vs| where Vs is stopping potential versus frequency f of the incident radiation.
(ii) State how will you use this graph to determine the value of Planck.s constant.
View Solution
Knowledge Check
A metallic surface is irradiated by a monochromatic light of frequency v1 and stopping potential is found to be V1. If the light of frequency v2 irradiates the surface, the stopping potential will be
AV1+he(v1+v2)BV1+he(v1−v2)CV1+eh(v2−v1)DV1−he(v1+v2)A metallic surface is irradiated by a monochromatic light of frequency v1 and stopping potential is found to be V1. If the light of frequency v2 irradiates the surface, the stopping potential will be
AV1+he(v1+v2)BV1+he(v2−v1)CV1+eh(v2−v1)DV1−he(v1+v2)
The emission of electrons from a metal surface exposed rto light radaition of appropriate wavelength is called photoelectroic effect .The emmited electron are called photo=-weklectron work function of threshold energy may be defined as the minimum amount of energy required to ejercted electron from a most surface .According to Einstein
Maximum kinetic energy of ejected electron = Aborbed energy - Work function
12mv2max=h(v)−h(vn)=hv[1λ−01λn]
Where vn and λ0 are thereshold frequency and threshold wavelength respectively
Sopping potential : it is the miximum potential at which the photoelectric current becomes zero if V0 is the stopping potential eV0=h(v−v0)
The stopping potential as a function on electron frtequency is plotted for two photoelectric surface A abd B The graph show that the work function of A is
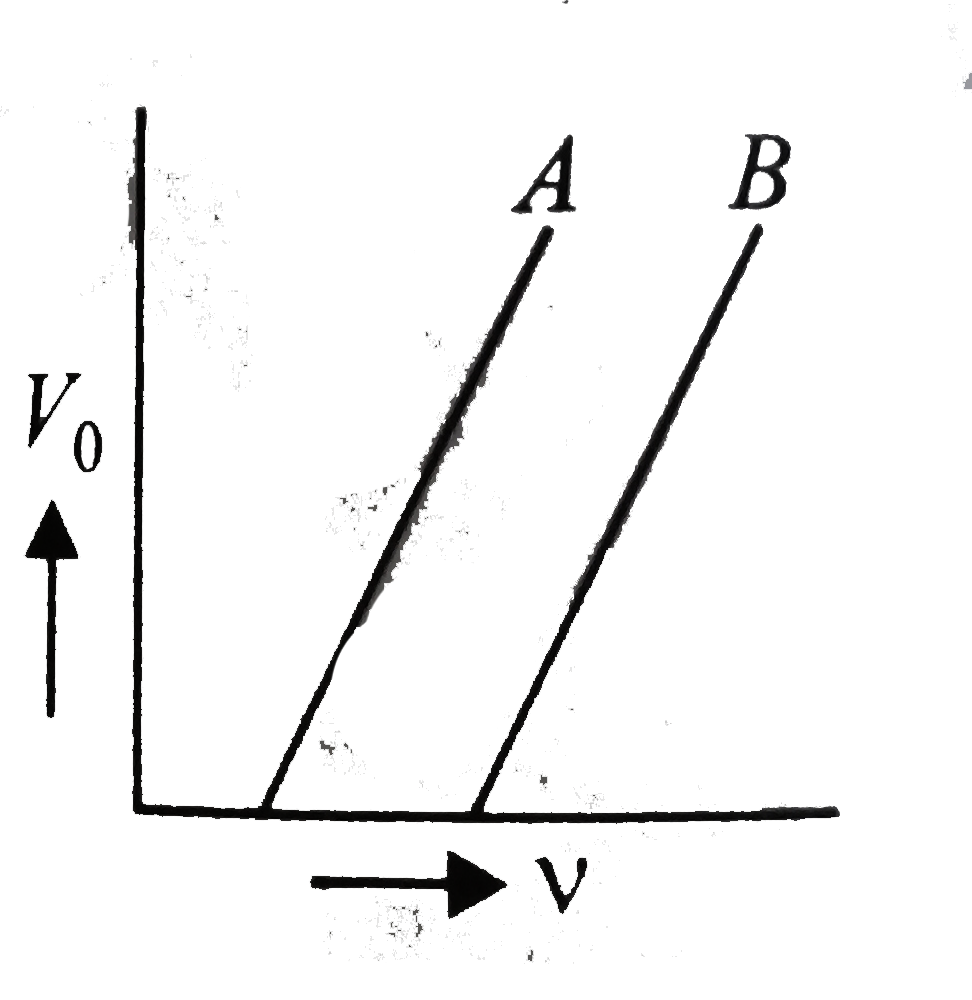
View SolutionThe ratio of slopes of Kmax vs. V and V0 vs. v curves in the photoelectric effect gives (v= freqency. Kmax= maximum kinetic energy, V0=stopping potential) :
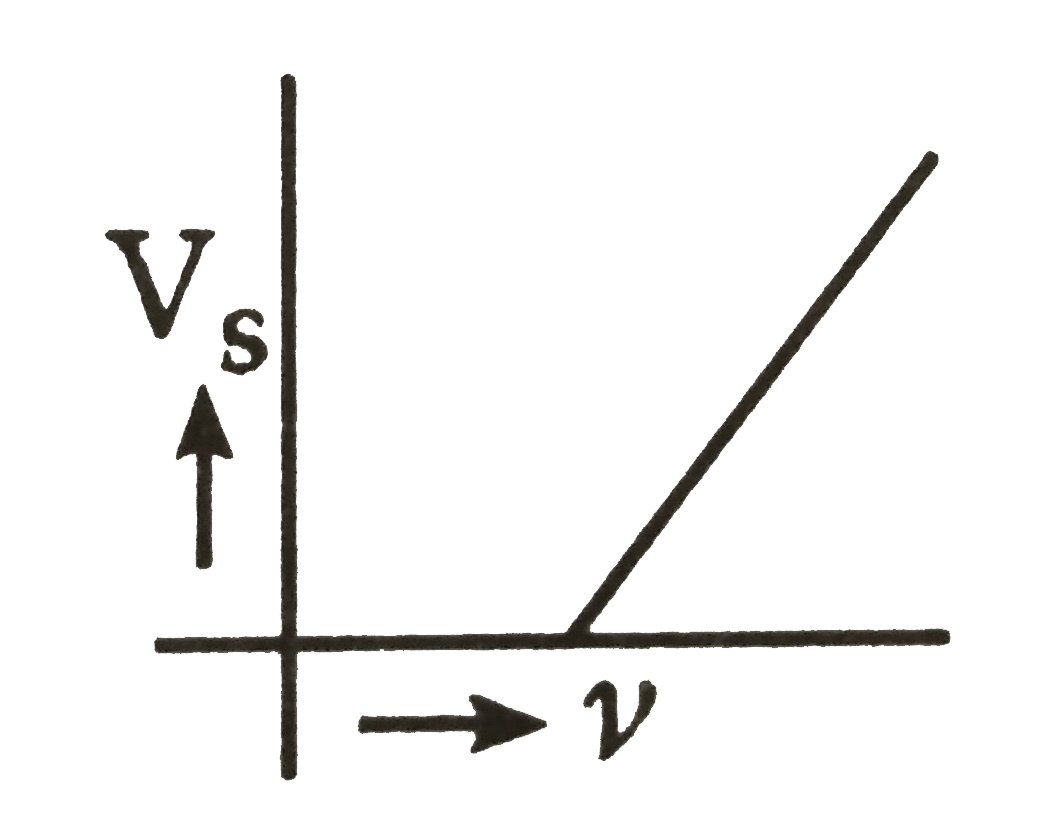
View SolutionIn photoelectric effect the slope of straight line graph between stopping potential (Vs) and frequency of incident light (v) gives
View SolutionWhen a certain photosensistive surface is illuminated with monochromatic light of frequency v, the stopping potential for the photo current is V0/2. When the surface is illuminated by monochromatic light of frequency v/2, the stopping potential is V0. The threshold frequency gor photoelectric emission is :
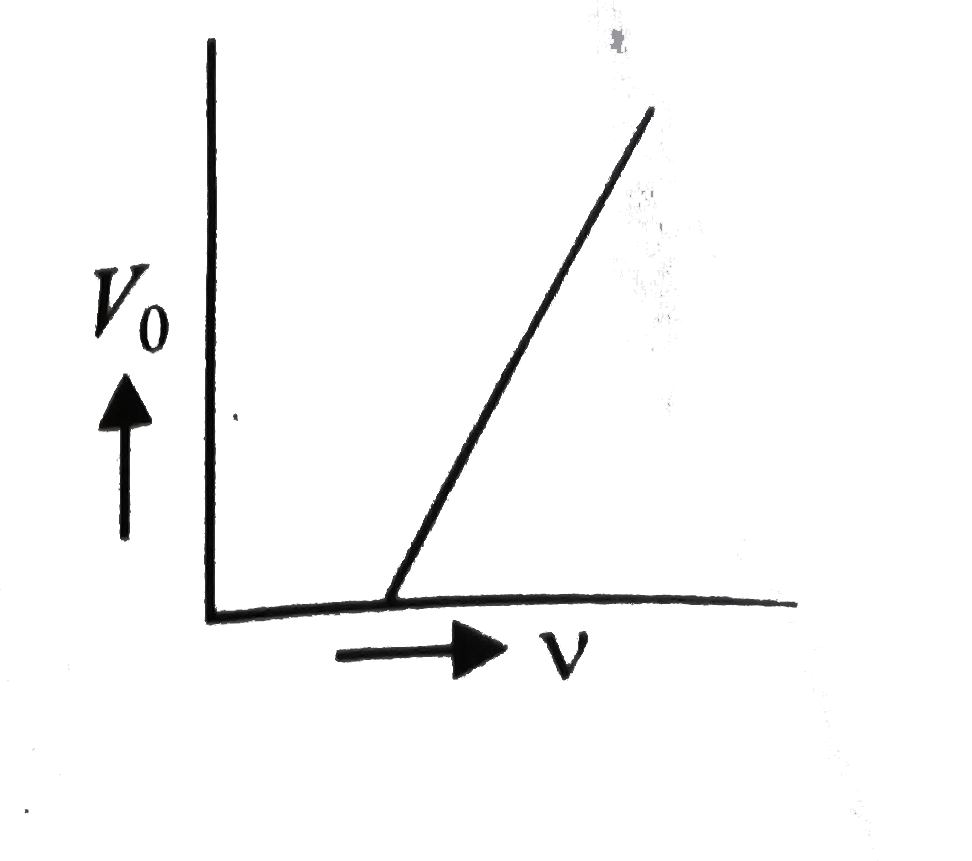
View SolutionThe emission of electrons from a metal surface exposed rto light radaition of appropriate wavelength is called photoelectric effect .The emmited electron are called photo=-weklectron work function of threshold energy may be defined as the minimum amount of energy required to ejected electron from a most surface .According to Einstein
Maximum kinetic energy of ejected electron = Absorbed energy - Work function
12mv2max=h(v)−h(vn)=hv[1λ−1λn]
Where vn and λ0 are thereshold frequency and threshold wavelength respectively
Sopping potential : it is the miximum potential at which the photoelectric current becomes zero if V0 is the stopping potential eV0=h(v−v0)
In the photoelectric currect effect the shape of strainght line graph between stopping potential (V0) and frequency of incident light (V) gves
View SolutionAssume that an electric field →E=30x2ˆi exists in space. Then the potential differences VA−V0 where V0 is the potential at the origin and VA, the potential at x=2m is
View Solution
