The variation of radial probability density R2 (r) as a function of distance r of the electron from the nucleus for 3p orbital:
(A)(a) 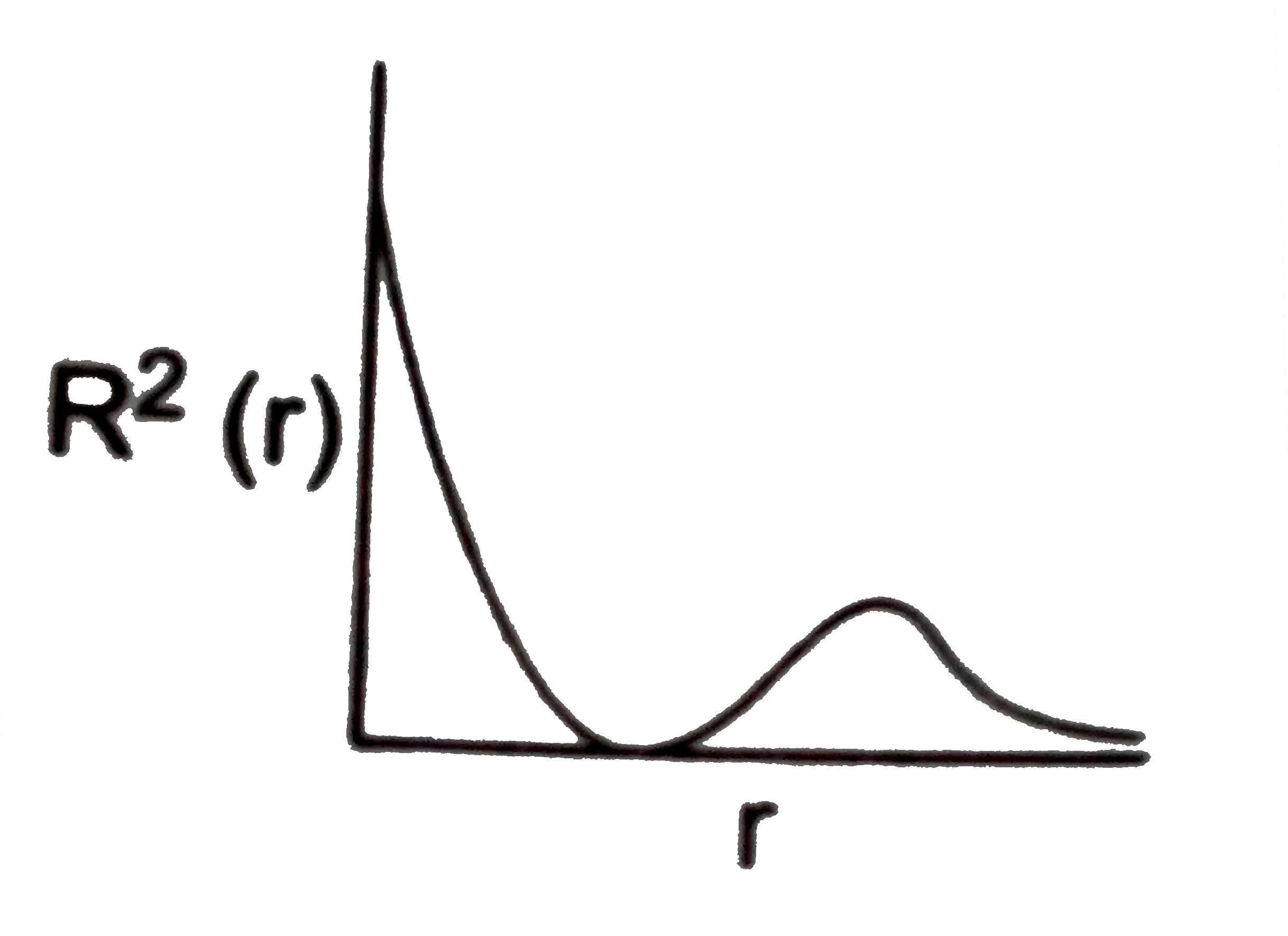
(b) (b) 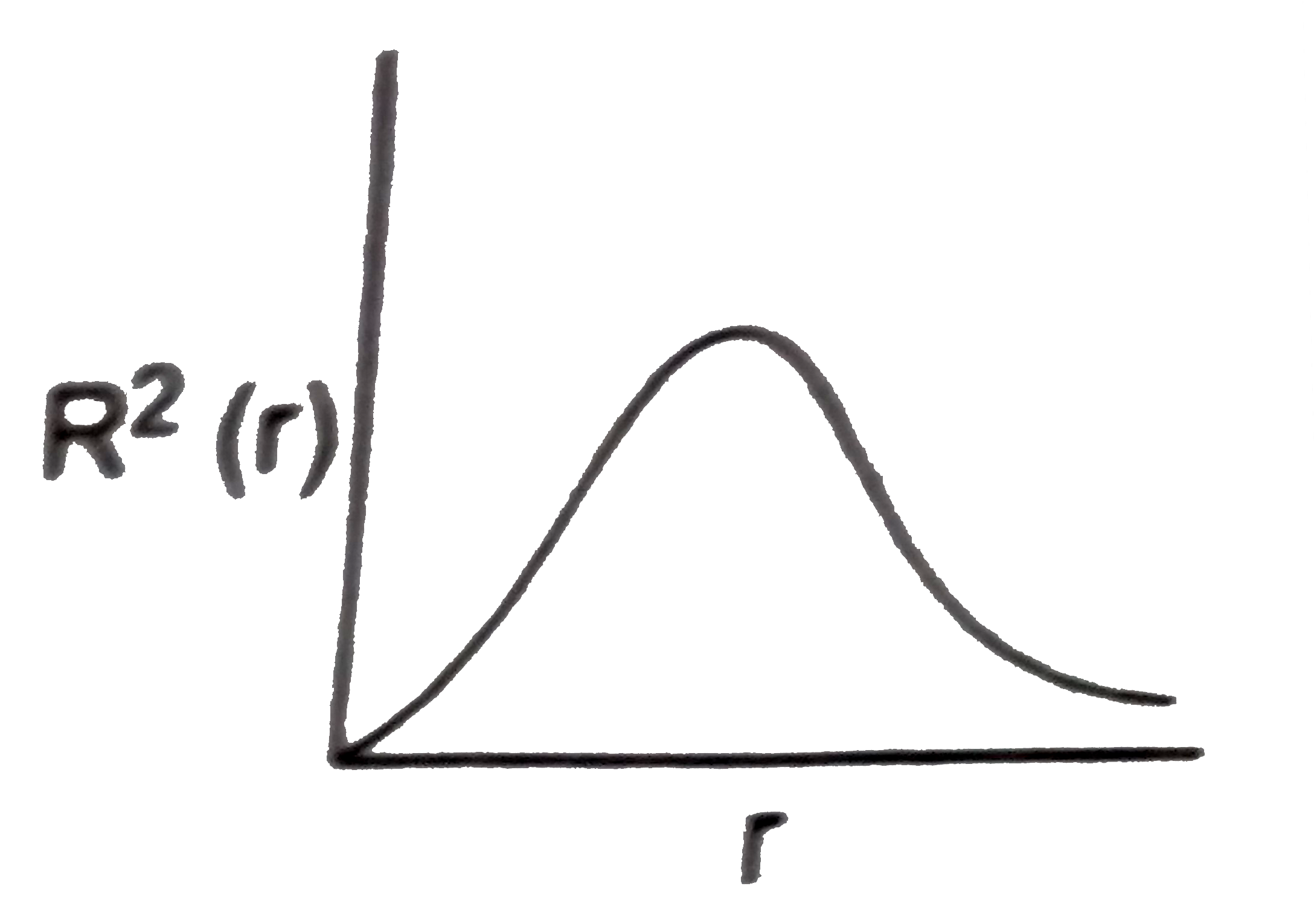
(c) 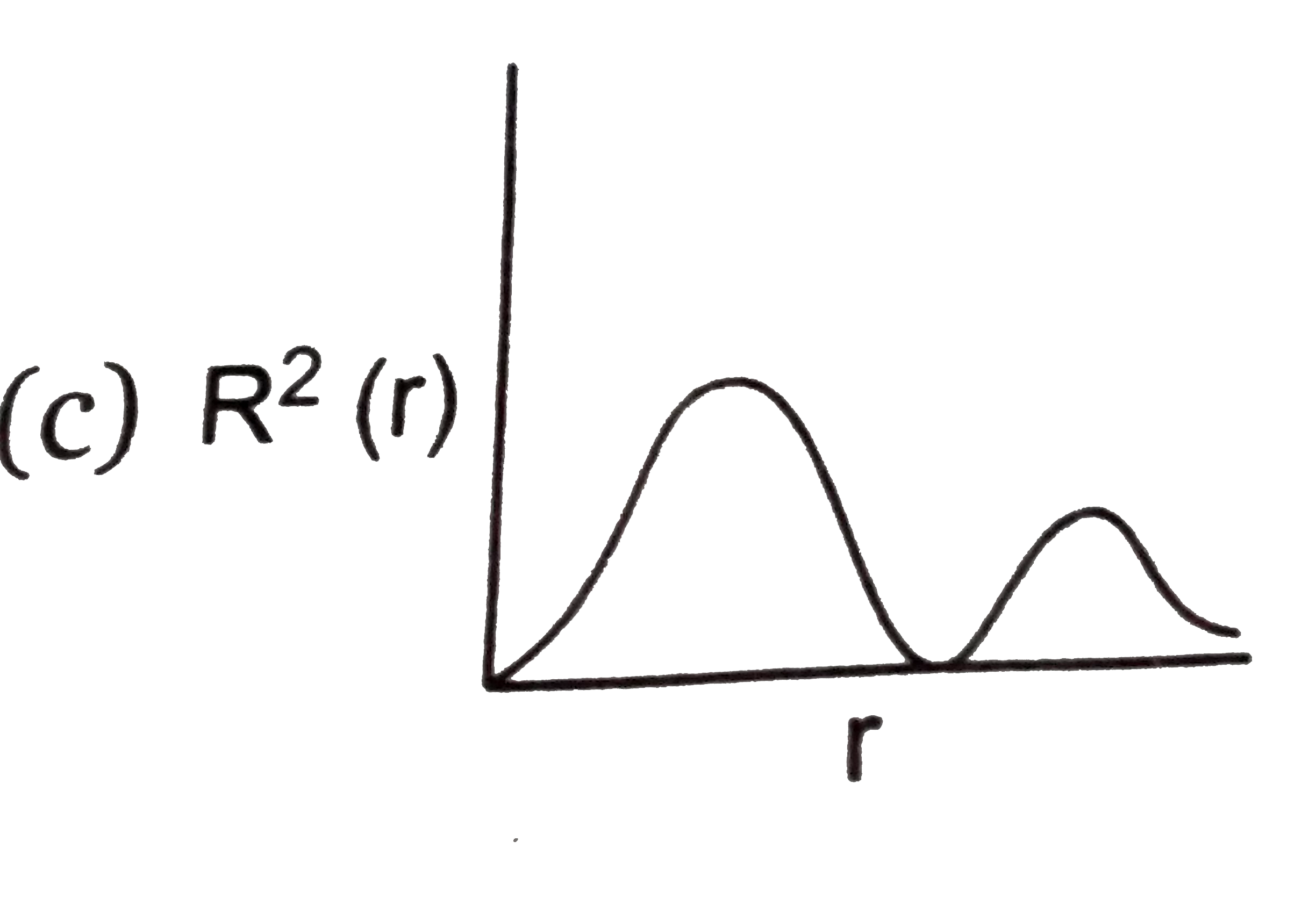
(d)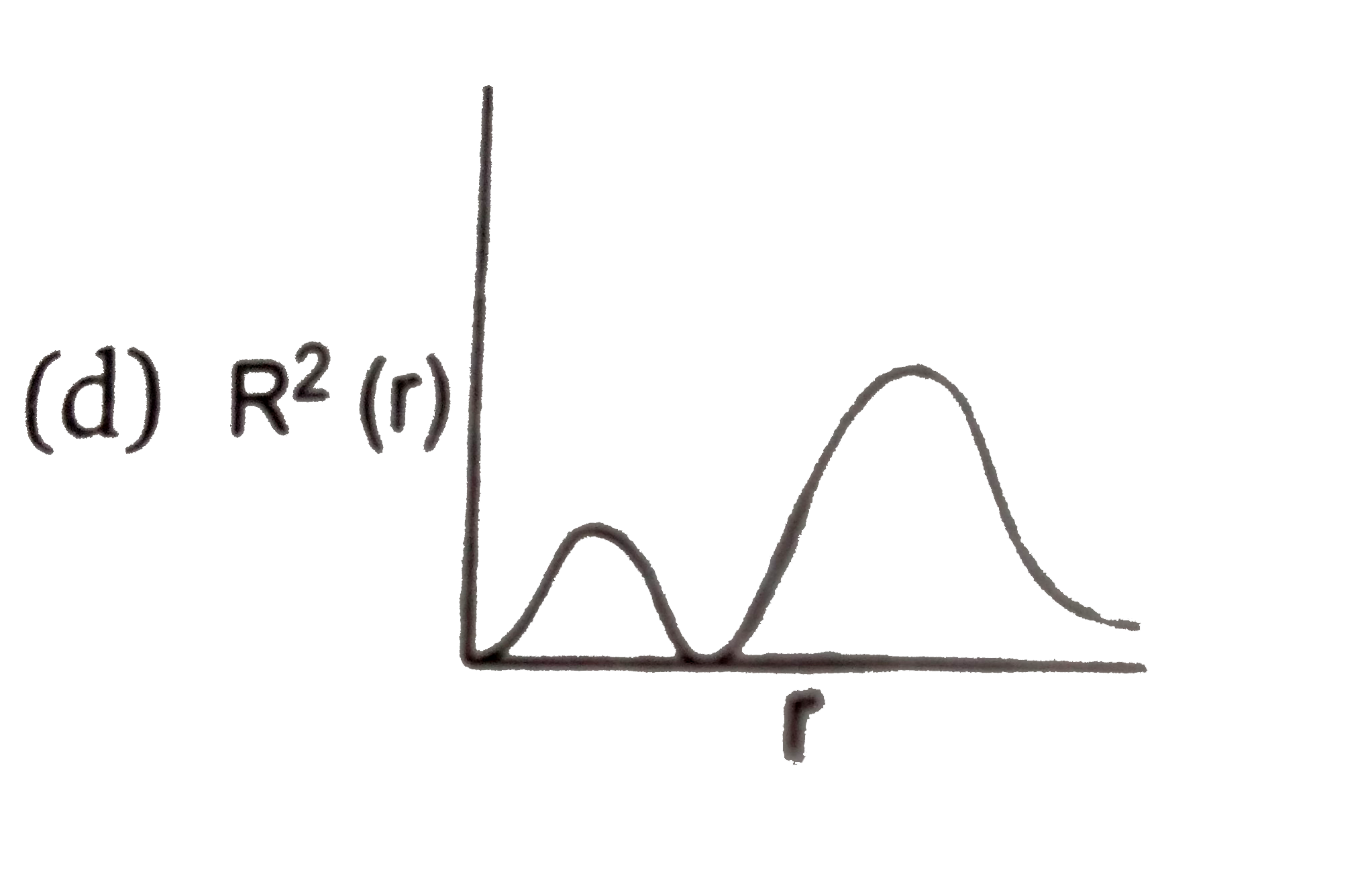
(a) 
(b) 


The correct Answer is:D
Step by step video & image solution for The variation of radial probability density R^2 (r) as a function of distance r of the electron from the nucleus for 3p orbital: (A)(a) (b) (b) (c) (d) by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - level 2
30 Videos
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - Level 3 (Passage 1)
3 Videos
- CHEMICAL EQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Match the column
1 Videos
Similar Questions
Knowledge Check
P is the probability of finding the Is electron of hydrogen atom in a spherical shell of infitesimal thickness, dr, at a distance r from the nucleus. The volume of this shell is 4πr2dr. The qualitative sketch of the dependence of P on r is
A B
B C
C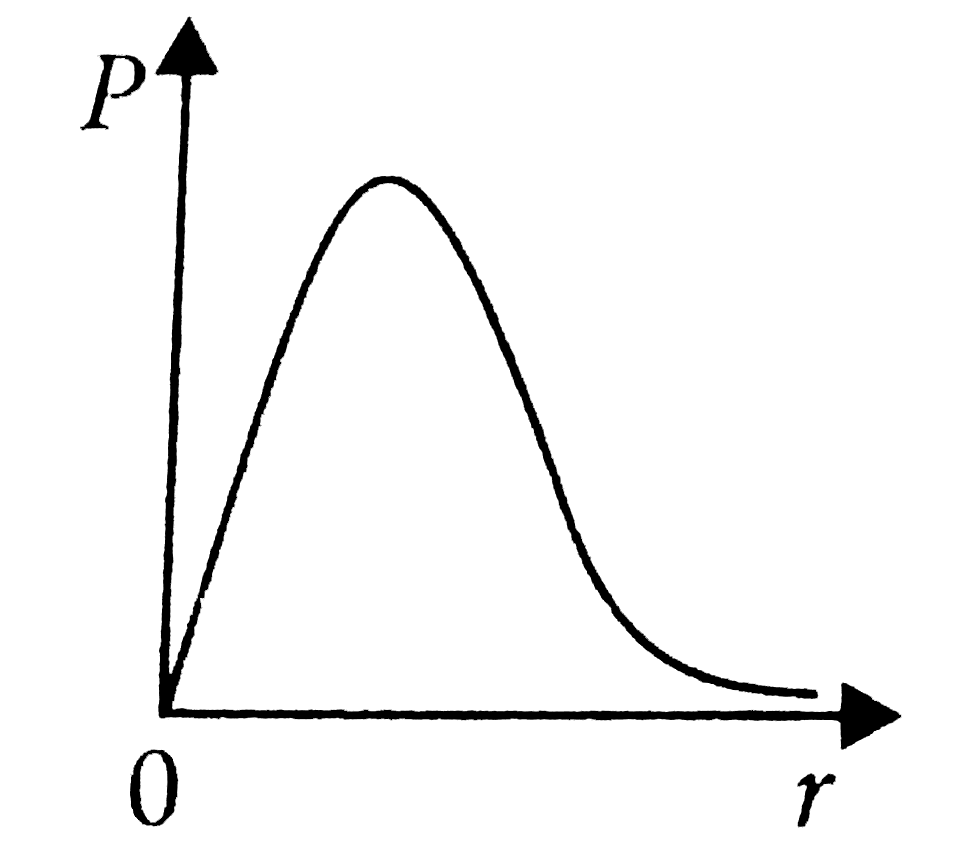 D
D
Select the correct plot of radial probability function (4πr2R2) for 2s - orbital.
View SolutionThe nuclear charge (Ze) is non uniformlly distribute with in a nucleus of radius r. The charge densilty ρ(r) (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
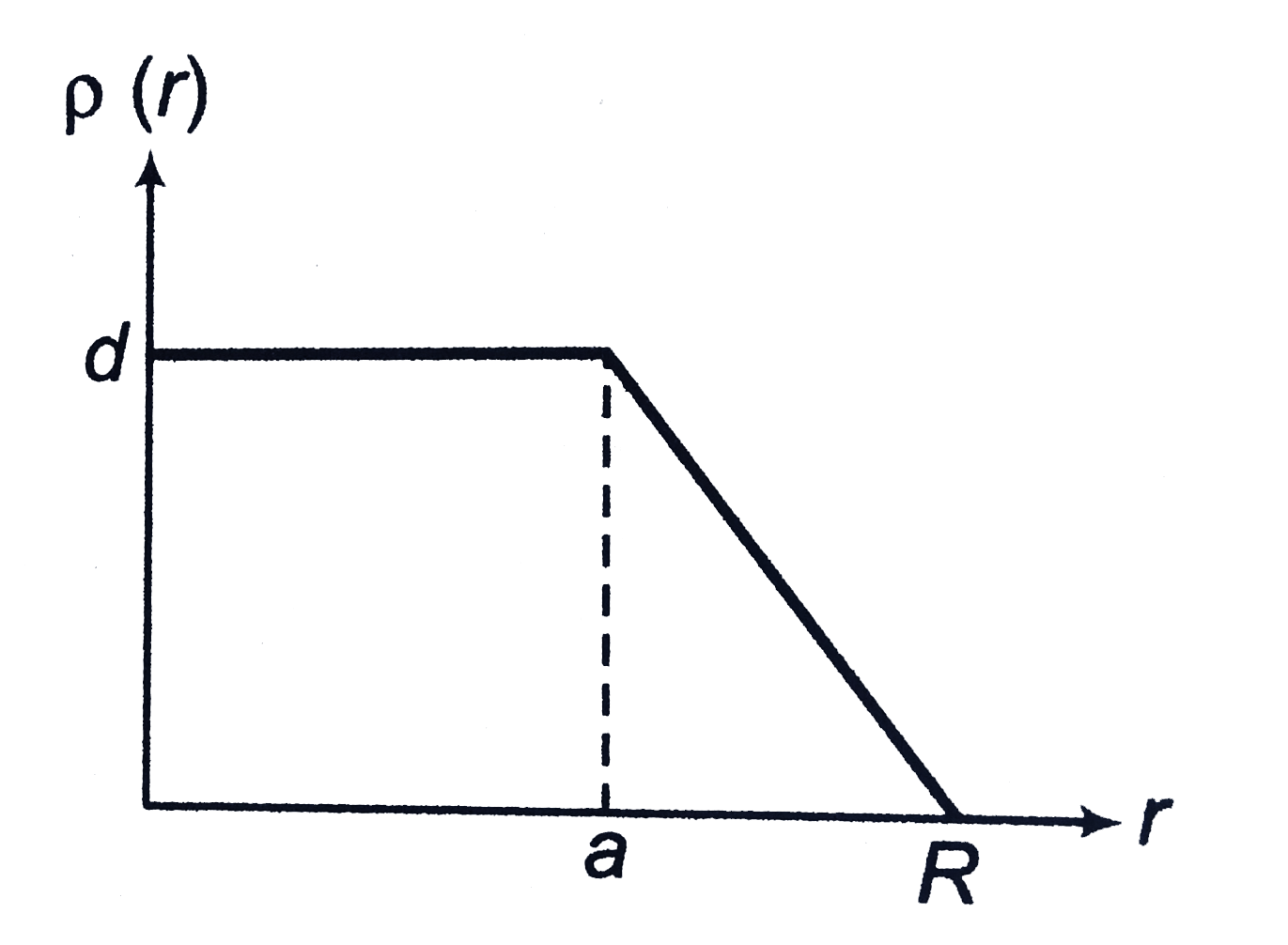
The electric field within the nucleus is generaly observed to be linearly dependent on r. This implies
View SolutionThe radial probability is the probability of finding electron in a small spherical shell around the nucleus at a particular distance r. Hence radial probability is
View SolutionA time varying uniform magnetic field passes through a circular region of radius R. The magnetic field is directed outwards and it is a function of radial distance 'r' and time 't' according to relation B-B_(0)rt. The induced electric field strength at a radial distance R/2 from the centre will be.
View SolutionAn infinitely long cylinderical wire of radius R is carrying a current with current density j=αr3 (where α is constant and r is the distance from the axis of the wire). If the magnetic fixed at r=R2 is B1 and at r=2R is B2 then the ratio B2B1 is
View SolutionPQ is a chord of parabola normal at P.Q. is the vertex and r the focus distance of P. If the line through P, parallel to AQ meets the axis in R, then AR= (A) r(B)2r(C)3r(D)r/2
View SolutionThe potential energy function of a particle is given by U(r)=A2r2−B3r, where A and B are constant and r is the radial distance from the centre of the force. Choose the correct option (s)
View Solution
