Which orbital has only positive value of wave function at all distances from the nucleus :
(a)1s
(b)2s
(c)3p
(d)3d
1s
2s
3p
3d
The correct Answer is:A
To determine which orbital has only positive values of the wave function at all distances from the nucleus, we can analyze the given options based on the properties of wave functions and nodes.
1. Understanding Wave Functions:
- The wave function (ψ) describes the probability amplitude of finding an electron in a given region of space. For an orbital to have only positive values of the wave function, it should not cross zero at any point (i.e., it should not have any nodes).
2. Identifying Radial Nodes:
- Radial nodes occur where the wave function equals zero. The number of radial nodes can be calculated using the formula:
Number of radial nodes=n−l−1
where n is the principal quantum number and l is the azimuthal quantum number.
3. Analyzing Each Option:
- (a) 1s:
- For 1s: n=1, l=0
- Radial nodes = 1−0−1=0 (No nodes, only positive values)
- (b) 2s:
- For 2s: n=2, l=0
- Radial nodes = 2−0−1=1 (One node, not all positive)
- (c) 3p:
- For 3p: n=3, l=1
- Radial nodes = 3−1−1=1 (One node, not all positive)
- (d) 3d:
- For 3d: n=3, l=2
- Radial nodes = 3−2−1=0 (No nodes, but 3d orbitals have angular nodes)
4. Conclusion:
- The only orbital that has no nodes and thus only positive values of the wave function at all distances from the nucleus is the 1s orbital.
Final Answer:
(a) 1s
- The wave function (ψ) describes the probability amplitude of finding an electron in a given region of space. For an orbital to have only positive values of the wave function, it should not cross zero at any point (i.e., it should not have any nodes).
- Radial nodes occur where the wave function equals zero. The number of radial nodes can be calculated using the formula:
Number of radial nodes=n−l−1
where n is the principal quantum number and l is the azimuthal quantum number.
- (a) 1s:
- For 1s: n=1, l=0
- Radial nodes = 1−0−1=0 (No nodes, only positive values)
- (b) 2s:
- For 2s: n=2, l=0
- Radial nodes = 2−0−1=1 (One node, not all positive)
- (c) 3p:
- For 3p: n=3, l=1
- Radial nodes = 3−1−1=1 (One node, not all positive)
- (d) 3d:
- For 3d: n=3, l=2
- Radial nodes = 3−2−1=0 (No nodes, but 3d orbitals have angular nodes)
- The only orbital that has no nodes and thus only positive values of the wave function at all distances from the nucleus is the 1s orbital.
(a) 1s
Topper's Solved these Questions
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - level 2
30 Videos
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - Level 3 (Passage 1)
3 Videos
- CHEMICAL EQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Match the column
1 Videos
Similar Questions
An orbital has only positive values of wave function at all distances from the nucleus. Find the value of (n+l) for this orbital.
View SolutionThe variation of radial probability density R2 (r) as a function of distance r of the electron from the nucleus for 3p orbital:
(A)(a)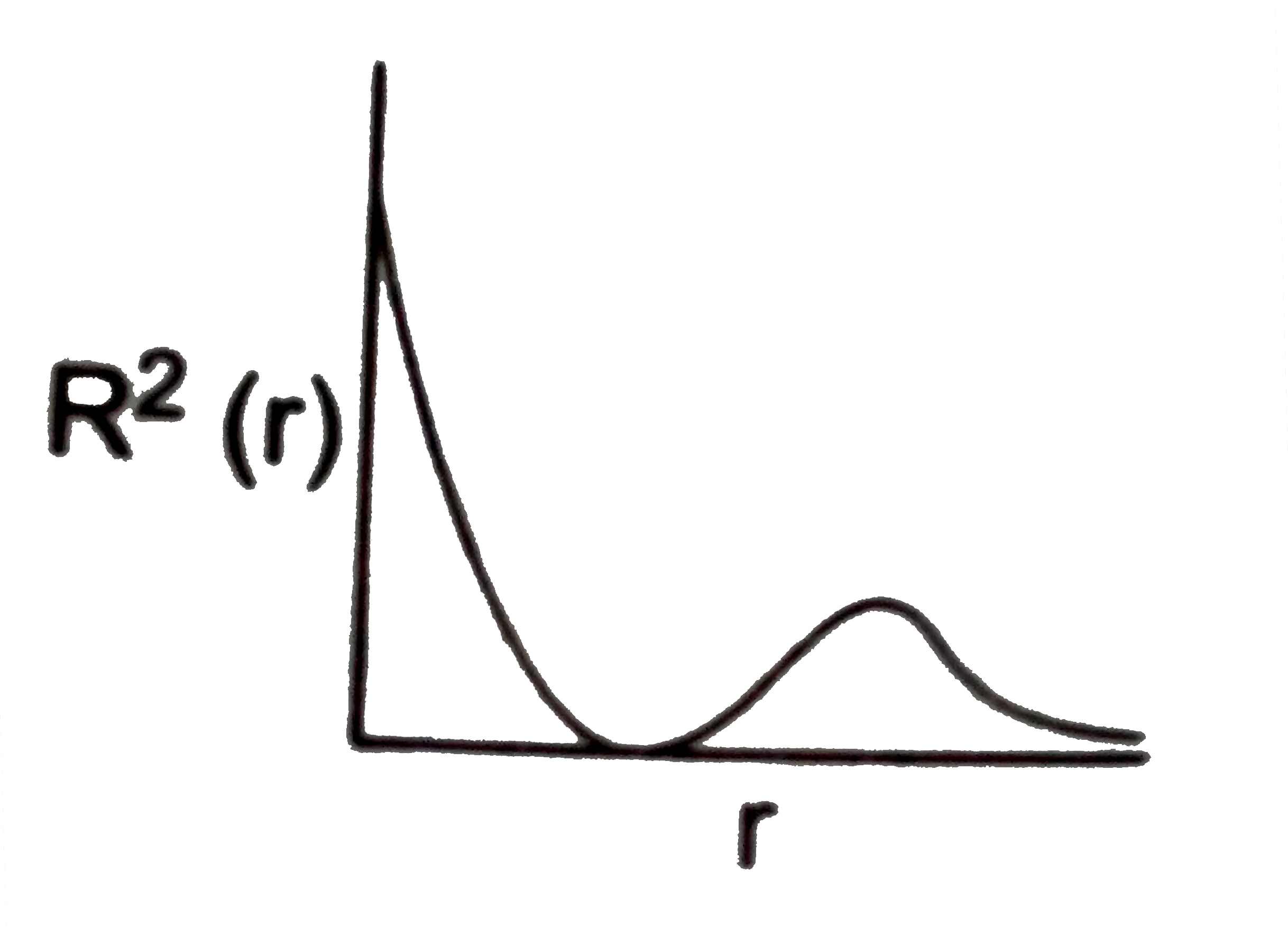
(b) (b)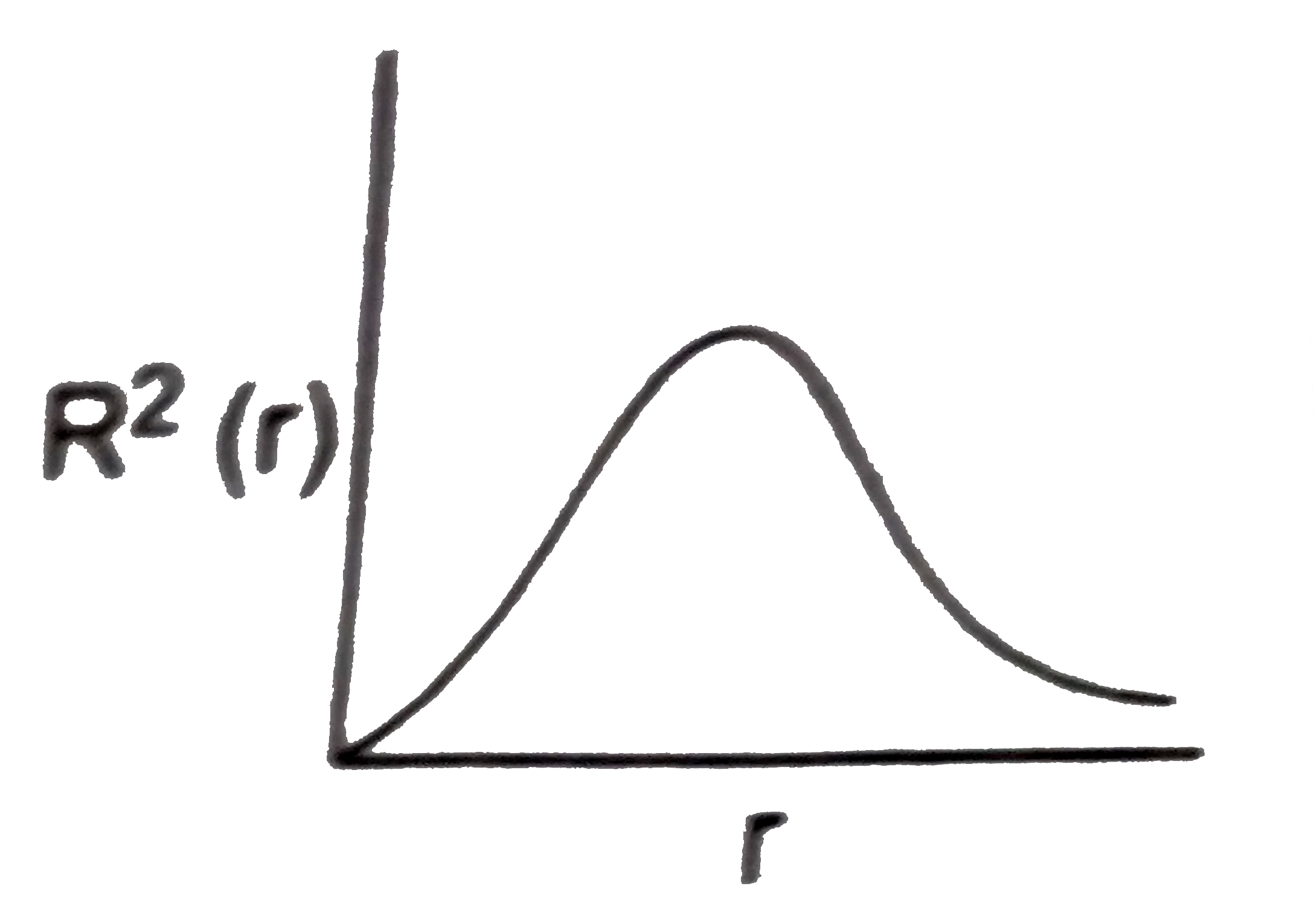
(c)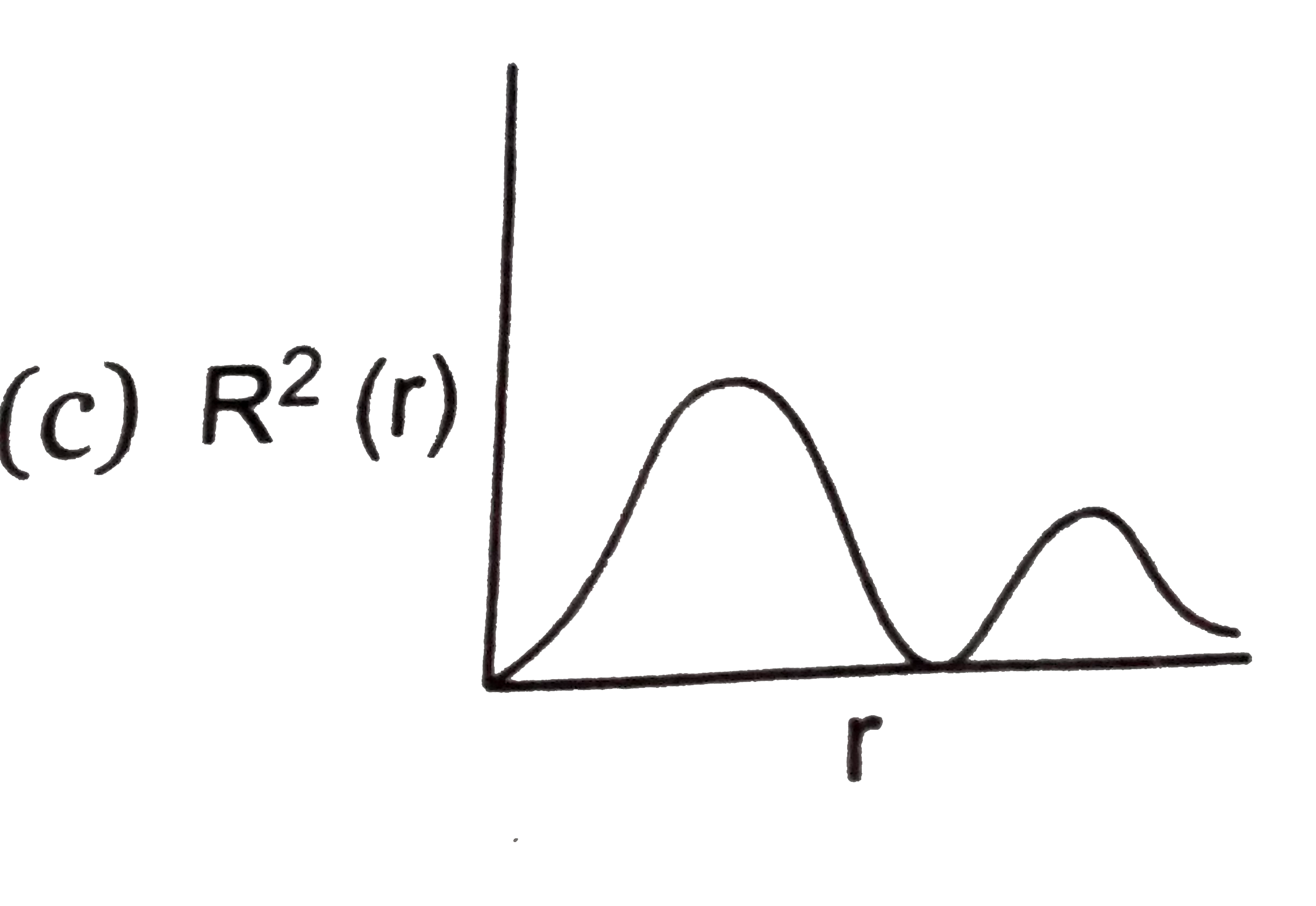
(d)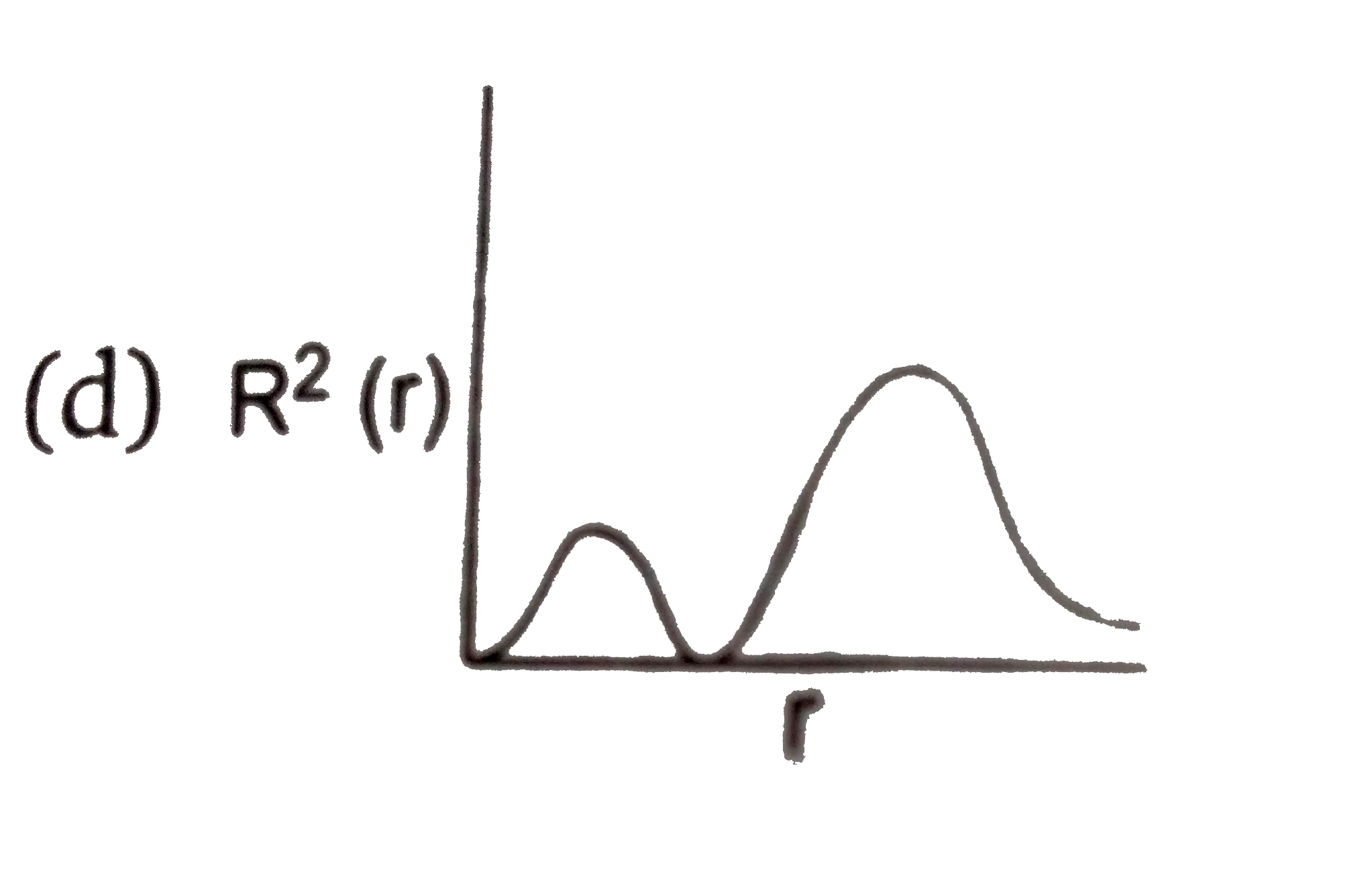
View SolutionMenstion the values of n and l corresponding to the following orbitals.
(a) 2s (b) 2p (c ) 3d (d) 4f ( e) 3s
View Solution4s orbitals has less energy than 3d orbital
View Solution4s orbitals has less energy than 3d orbital
View Solutiona. An atomic orbital has n=3. What are the possible values of l and m?
b. List the quantum numbers (mandl) of electrons for 3d orbital.
c. Which of the following orbitals are possible" 1p,2s,2p, and 3f?
View SolutionWave function of an orbital is plotted against the distance from nucleus
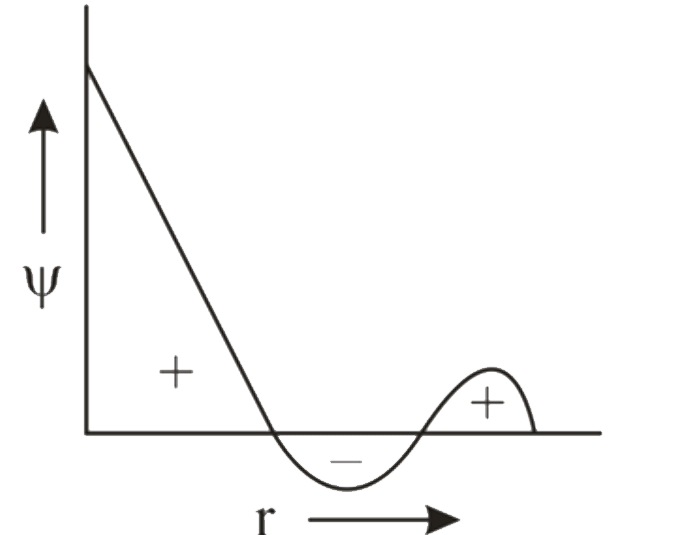
The graphical representation is of
View SolutionThe correct order of closeness of 3s,3p,3d orbitals of nucleus is :
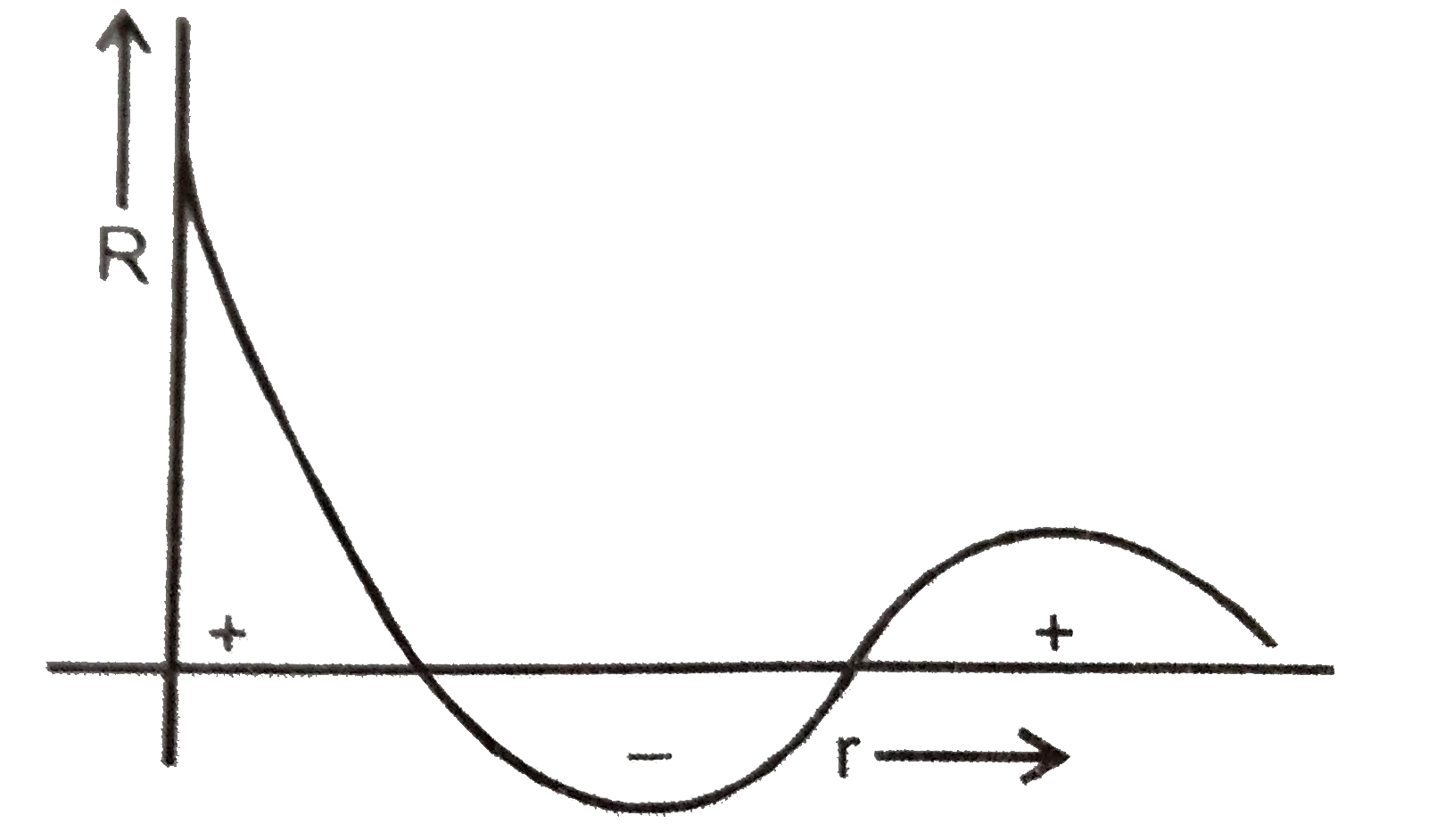
View SolutionWave function of an orbital is plotted against the distance from nucleus. The graphical representation is of :
View SolutionArrange the following orbitals of H-atom in the increasing order of their energy.
3px,2s,4dxy,3s,4pz,3py,4s
View Solution
