If concentration of two weak bases are same and D.O.D (α) are very less their ralative strength can be compared by :
[OH−]1[OH−]2
Kb1Kb2
α1α2
√Kb1√Kb2
The correct Answer is:D
To solve the problem of comparing the relative strength of two weak bases with the same concentration and very low degrees of dissociation, we can follow these steps:
1. Understanding Weak Bases:
- Weak bases partially dissociate in solution. For example, if we have two weak bases, AOH and BOH, they dissociate as follows:
- AOH ⇌ A⁺ + OH⁻
- BOH ⇌ B⁺ + OH⁻
2. Concentration and Degree of Dissociation:
- Let the concentration of both bases be C molar.
- Let the degree of dissociation (α) for AOH be α₁ and for BOH be α₂. Since the degrees of dissociation are very small, we can assume that the concentration of undissociated base is approximately equal to C (i.e., 1 - α ≈ 1).
3. Calculating Concentrations of Ions:
- The concentration of hydroxide ions (OH⁻) produced by each base can be expressed as:
- For AOH: (OH⁻) = Cα₁
- For BOH: (OH⁻) = Cα₂
4. Equilibrium Constants:
- The base dissociation constant (K_b) for each base can be expressed as:
- K_b₁ = (A⁺)(OH⁻) / (AOH) = (Cα₁)(Cα₁) / (C(1 - α₁)) ≈ Cα₁² (since α₁ is small)
- K_b₂ = (B⁺)(OH⁻) / (BOH) = (Cα₂)(Cα₂) / (C(1 - α₂)) ≈ Cα₂²
5. Relating K_b Values:
- From the above, we have:
- K_b₁ ≈ Cα₁²
- K_b₂ ≈ Cα₂²
- Therefore, we can relate the two constants:
- K_b₁ / K_b₂ = (Cα₁²) / (Cα₂²) = α₁² / α₂²
6. Comparing Relative Strengths:
- The relative strength of the bases can be compared using the concentration of hydroxide ions produced:
- Relative strength = (OH⁻)₁ / (OH⁻)₂ = (Cα₁) / (Cα₂) = α₁ / α₂
- Thus, we can conclude that:
- α₁ / α₂ = K_b₁ / K_b₂
7. Final Conclusion:
- Since K_b values are directly related to the strength of the bases, we can compare the relative strength of the two weak bases based on their K_b values.
- Weak bases partially dissociate in solution. For example, if we have two weak bases, AOH and BOH, they dissociate as follows:
- AOH ⇌ A⁺ + OH⁻
- BOH ⇌ B⁺ + OH⁻
- Let the concentration of both bases be C molar.
- Let the degree of dissociation (α) for AOH be α₁ and for BOH be α₂. Since the degrees of dissociation are very small, we can assume that the concentration of undissociated base is approximately equal to C (i.e., 1 - α ≈ 1).
- The concentration of hydroxide ions (OH⁻) produced by each base can be expressed as:
- For AOH: (OH⁻) = Cα₁
- For BOH: (OH⁻) = Cα₂
- The base dissociation constant (K_b) for each base can be expressed as:
- K_b₁ = (A⁺)(OH⁻) / (AOH) = (Cα₁)(Cα₁) / (C(1 - α₁)) ≈ Cα₁² (since α₁ is small)
- K_b₂ = (B⁺)(OH⁻) / (BOH) = (Cα₂)(Cα₂) / (C(1 - α₂)) ≈ Cα₂²
- From the above, we have:
- K_b₁ ≈ Cα₁²
- K_b₂ ≈ Cα₂²
- Therefore, we can relate the two constants:
- K_b₁ / K_b₂ = (Cα₁²) / (Cα₂²) = α₁² / α₂²
- The relative strength of the bases can be compared using the concentration of hydroxide ions produced:
- Relative strength = (OH⁻)₁ / (OH⁻)₂ = (Cα₁) / (Cα₂) = α₁ / α₂
- Thus, we can conclude that:
- α₁ / α₂ = K_b₁ / K_b₂
- Since K_b values are directly related to the strength of the bases, we can compare the relative strength of the two weak bases based on their K_b values.
Similar Questions
If concentration of two weak acids are different and D.O.D (α) are very less then their relative strngth can be compared by :
View SolutionIf the concentration of two monobasic acids are same, their relative strength can be compared by
View SolutionStatement-1: pH value of acidic buffer solution changes , If buffer solution is diluted upto very large extent.
Statement-2: [H+] decreases due to change in concentration as well as α increases and decreases in concentration is more as compared to increases in α .
View SolutionIf a charged particle of charge to mass ratio (qm)=α centers in a magnetic field of strength B at a speed v=(2αd)(B), then

View SolutionThe extent to which hydrolysis proceeds is expressed as degree of hydrolysis and is defined as fraction of ne mole of the salt that is hydrolysed when equilibrium has been attained . The nature of solution also depends upon the extent upto which the salt has been hydrolysed . Degree of hydrolysis of a salt ofdepends upon concentration of salt at a particular temperature and varies inversely . Consequently , nature of the solution whether acidic or alkaline can be determined . pH of the solution of salt of weak acid and strong base or weak base and strong acid depends upon its concentration . So by varying the concentration of salts their pH could be adjusted .
For strong acid and weak base salt solution , the [H3O+] at equilibrium will be
View SolutionThe extent to which hydrolysis proceeds is expressed as degree of hydrolysis and is defined as fraction of ne mole of the salt that is hydrolysed when equilibrium has been attained . The nature of solution also depends upon the extent upto which the salt has been hydrolysed . Degree of hydrolysis of a salt ofdepends upon concentration of salt at a particular temperature and varies inversely . Consequently , nature of the solution whether acidic or alkaline can be determined . pH of the solution of salt of weak acid and strong base or weak base and strong acid depends upon its concentration . So by varying the concentration of salts their pH could be adjusted .
For strong base and weak acid litration , the [H3O+] at equivalence point will be
View SolutionIf degree of ionization (α) of a weak electrolyte AB is very less then α is :
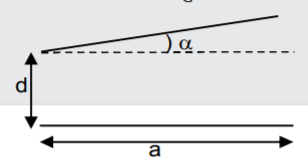
View SolutionTwo square plates of side 'a' are arranged as shown in the figure. The minimum separation between plates is 'd' and one of the plate is inclined at small angle α with plane parallel to another plate. The capacitance of capacitor is (given α is very small)
View SolutionThe degree of dissociation of weak electrolyde is inversely proportional to the square root fo concentration. It is called Ostwald's dilution law.
α=√Kac As the tempertaure increases, degree of dissociation will increase.
α1α2=√Ka1Ka2 if concentration is same.
α1α2=√c2c1 if acid is same.
pH of 0.005MHCOOH[Ka=2×10−4] is equal to
View SolutionIf at same temperature and pressure, the densities for two diatomic gases are respectively d1andd2 , then the ratio of velocities of sound in these gases will be
View Solution
