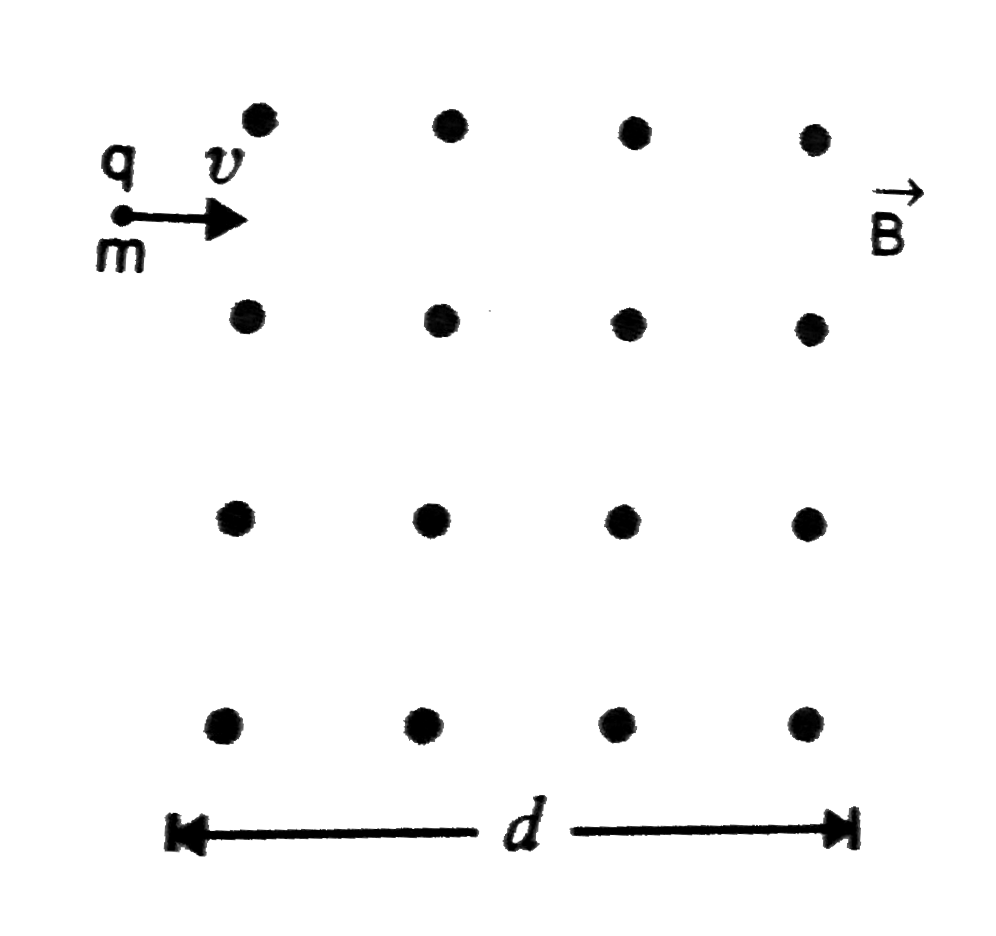
If a charged particle of charge to mass ratio (qm)=α centers in a magnetic field of strength B at a speed v=(2αd)(B), then

angle subtended by the path of charged particle in magnetic field at the centre of circular path is 2π
The charge will move on a circular path and then will come out from magnetic field at some distance from the point of indertion
The time for which particle will be in the magnetic field is 2παB
Angle subtended by the path of charged particle in magnetic field at the centre of circular path is π/2
The correct Answer is:b
r=mvqB=vBα=(2αd)(B)(Bα)=2d

i.e., the electron will move out after travelling on a semicircular path of radius r=2d.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Multiple Correct
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Assertion -reasoning
8 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Subjective
10 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
In the figure shown a positively charged particle of charge q and mass m enters into a uniform magnetic field of strength B as shown in the figure.The magnetic field points inwards and is present only within a region of width d.The initial velocity of the particle is perpendicular to the magnetic field and ϕ=30∘.Find the time spent by the particle inside the magnetic field if d=0.2m,B=1T,q=1C,m=1kg and v=1m/s.Use sin45∘=0.7 if required .

View SolutionA charged particle with charge to mass ratio (qm)=(10)319Ckg−1 enters a uniform magnetic field →B=20ˆi+30ˆj+50ˆkT at time t = 0 with velocity →V=(20ˆi+50ˆj+30ˆk)m/s. Assume that magnetic field exists in large space.
During the further motion of the particle in the magnetic field, the angle between the magnetic field and velocity of the particle
View SolutionA charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B the frequency of revolution is
View SolutionA charged particle of charge q and mass m enters perpendiculalry in a magnetic field B. Kinetic energy of particle is E, then frequency of rotation is
View SolutionA charged particle of mass m and charge q is projected into a uniform magnetic field of induciton →B with speed v which is perpendicular to →B. The width of the magnetic field is d. The impulse imparted to the particle by the field is (d<<mv/qB)
View SolutionA charge particle of charge 'q' and mass 'm' enters in a given magnetic field 'B' and perpendicular to the magnetic field as shown in the figure. It enters at an angle of 60∘ with the boundary surface of magnetic field and comes out at an angle of 30∘ with the boundary surface of the magnetic field as shown in the figure. Find width 'd' in which magnetic field exist.

View SolutionA charged particle of charge 1 mC and mass 2g is moving with a speed of 5m/s in a uniform magnetic field of 0.5 tesla. Find the maximum acceleration of the charged particle
View SolutionA charged particle of charge 1 mC and mass 2g is moving with a speed of 5m/s in a uniform magnetic field of 0.5 tesla. Find the maximum acceleration of the charged particle
View SolutionA positive charge particle having change q and mass m has velocity →v=v(ˆi+ˆk√2) in the magnetic field B at the origin . Its speed as the function of y is :
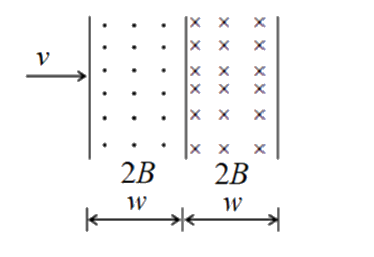
View SolutionThe figure shows two regions of uniform magnetic field of strengths 2B and 2B. A charged particle of mass m and charge q enters the region of the magnetic field with a velocity υ=qBwm, where w is the width of each region of the magnetic field. The time taken by the particle to come out of the region of the magnetic field is
View Solution
