Two glass bulbs A and B are connected by a very small tube having a stop cock. Bulb A has a volume of 100 cm3 and contained the gas, while bulb B was empty. On opening th stop cock. The pressure fell down to 40%. The volume of the bulb B must be:
100cm3
200cm3
250cm3
400cm3
The correct Answer is:d
To solve the problem, we need to apply the ideal gas law and the concept of pressure-volume relationships. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have two glass bulbs, A and B. Bulb A has a volume of 100 cm³ and contains gas, while bulb B is empty. When the stopcock is opened, the gas from bulb A will expand into bulb B.
Step 2: Apply the Ideal Gas Law
According to the ideal gas law, for a given amount of gas at constant temperature, the product of pressure and volume is constant:
P1V1=P2V2
Where:
- P1 = initial pressure in bulb A
- V1 = volume of bulb A (100 cm³)
- P2 = final pressure after opening the stopcock (40% of P1)
- V2 = volume of bulb B (which we need to find)
Step 3: Express the Pressures
Let’s denote the initial pressure in bulb A as P1=k. Then, the final pressure P2 after the stopcock is opened is:
P2=0.4k
Step 4: Set Up the Equation
Substituting the known values into the equation:
P1V1=P2(V1+V2)
This becomes:
k⋅100=0.4k⋅(100+V2)
Step 5: Simplify the Equation
We can cancel k from both sides (assuming k≠0):
100=0.4(100+V2)
Step 6: Distribute and Rearrange
Distributing 0.4:
100=40+0.4V2
Now, subtract 40 from both sides:
60=0.4V2
Step 7: Solve for V2
To find V2, divide both sides by 0.4:
V2=600.4=150 cm3
Step 8: Calculate Total Volume
The total volume when the gas expands into bulb B is:
Vtotal=V1+V2=100+150=250 cm3
Final Answer
The volume of bulb B must be:
VB=150 cm3
We have two glass bulbs, A and B. Bulb A has a volume of 100 cm³ and contains gas, while bulb B is empty. When the stopcock is opened, the gas from bulb A will expand into bulb B.
According to the ideal gas law, for a given amount of gas at constant temperature, the product of pressure and volume is constant:
P1V1=P2V2
- P1 = initial pressure in bulb A
- V1 = volume of bulb A (100 cm³)
- P2 = final pressure after opening the stopcock (40% of P1)
- V2 = volume of bulb B (which we need to find)
Let’s denote the initial pressure in bulb A as P1=k. Then, the final pressure P2 after the stopcock is opened is:
P2=0.4k
Substituting the known values into the equation:
P1V1=P2(V1+V2)
This becomes:
k⋅100=0.4k⋅(100+V2)
We can cancel k from both sides (assuming k≠0):
100=0.4(100+V2)
Distributing 0.4:
100=40+0.4V2
Now, subtract 40 from both sides:
60=0.4V2
To find V2, divide both sides by 0.4:
V2=600.4=150 cm3
The total volume when the gas expands into bulb B is:
Vtotal=V1+V2=100+150=250 cm3
The volume of bulb B must be:
VB=150 cm3
Topper's Solved these Questions
- GASEOUS STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 2
30 Videos
- GASEOUS STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 3 Passage 1
4 Videos
- ELECTROCHEMISTRYBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Subjective problems
14 Videos
- IONIC EEQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - IONIC EEQUILIBRIUMEXERCISE - Subjective problems
1 Videos
Similar Questions
Two glass bulbs x and y are connected by a very small tube having a stop - cock. Bulb X has a volume of 100cm3 and contained the gas, while bulb Y was empty. On opening the stop - cock, the pressure fell down to 60%. The volume of the bulb Y must be
View SolutionInitially bulb "a" contained oxygen gas at 27∘C and 950 mm of Hg and bulb "B" contained neon gas at 27∘C and 900 mm of Hg. These bulbs are connected by a narrow tube of negligible volume equipped with a stopcock and gases were allowed to mix-up freely. The pressure obtained in the combined system was found to be 910 mm of Hg.

If volume of bulb B was measured to be 10 L, then find the volume of oxygen gas present initially in bulb "A" .
View SolutionTwo glass bulbs of same volume containing a gas at NTP are connected by a very narrow tube. The pressure is 88.46cm of mercury when one bulb is kept in ice and the other in hot water. Calculate the temperature of the hot water.
View SolutionTwo electric bulbs A and B are rated as 60 W and 100 W . They are connected in parallel to the same source. Then,
View Solutiontwo glass bulbs of equal volume are connected by a narrow tube and are filled with a gas at 0(∘)C at a pressure of 76cm of mercury. One of the bulbs is then placed in melting ice and the other is placed in a water bath maintained at 62∘C.What is the new value of the pressure inside the bulbs? The volume of the connecting tube is neigligible.
View SolutionTwo cylinders A and B of equal capacity are connected to each other via a stop cock. Cylinder A contains an ideal gas at standard temperature and pressure. Cylinder B is completely evacuated. The entire system is thermally insulated. The stop cock is suddenly opened. The process is:
View SolutionA bulb A containing gas at 1.5 bar pressure was connected to an evacuated vessel of 1.0 dm3 capacity through a stopcock. The final pressure of the system dropped to 920 mbar at the same temperature. What is the volume of the container A?
View SolutionA tube of fine bore AB is connected to a manomeer M as shown. The stop cock S controls the flow in air. AB is dipped into a liquid whosw surface tension is σ. On opening the stop cock for a while, a bubble is formed at B and the manometer level is recorded, showing a difference h in the levels in the two arms. If ρ be the density of manometer liquid and r the radius of curvature of the bubble, then the surface tension σ of the liquid is given by

View SolutionTwo closed bulbs of equal volume (V) containing an ideal gas initially at pressure Pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below . The temperature of one of the bulbs is then raised to T2 . the final pressure Pf is
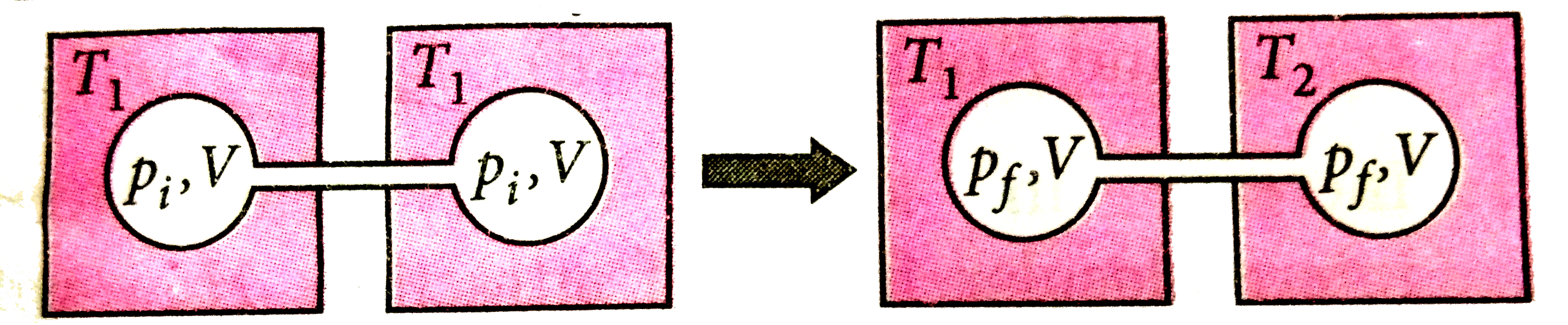
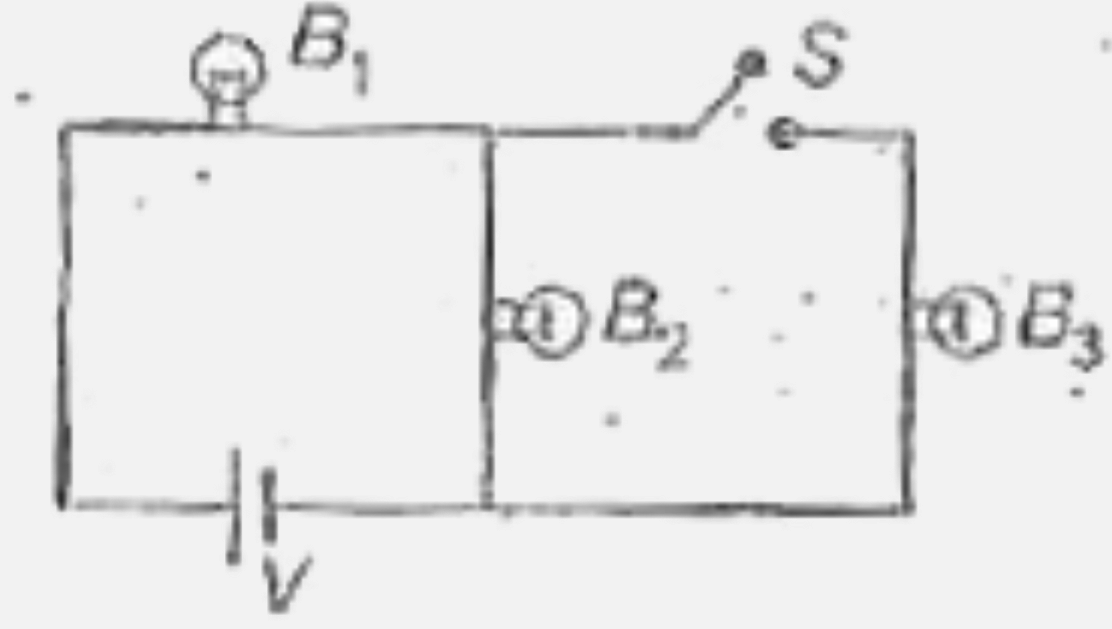
View SolutionThree identical bulbs B1,B2 and B3 are connected to the mains as shown in figure. If B3 is disconnected for the from the circuit by opening switch S, then incandescence of bulb B1 will . ,
View Solution
