A body weighing 13 kg is suspended by two strings 5 m and 12 m long, their other ends being fastened to the extremities of a rod 13 m long. If the rod be so held that the body hangs immediately below the middle point. The tensions in the strings are (1) 12 kg and 13 kg (2) 5 kg and 5 kg (3) 5 kg and 12 kg (4) 5 kg and 13 kg
To solve the problem, we need to find the tensions in the two strings supporting the body. Let's denote the tensions in the strings as T1 (for the string of length 5 m) and T2 (for the string of length 12 m).
1. Understanding the Setup:
- We have a body weighing 13 kg suspended by two strings of lengths 5 m and 12 m.
- The rod connecting the two strings is 13 m long, and the body hangs directly below the midpoint of the rod.
2. Drawing the Diagram:
- Draw a triangle where:
- A and B are the ends of the rod (13 m apart).
- O is the point where the body is suspended.
- OA=12 m (length of the first string).
- OB=5 m (length of the second string).
- The triangle AOB is formed with AB=13 m.
3. Using the Pythagorean Theorem:
- Since the body hangs directly below the midpoint, we can apply the Pythagorean theorem:
AB2=OA2+OB2
132=122+52
169=144+25
169=169
- This confirms that the triangle is a right triangle with ∠AOB=90∘.
4. Finding the Angles:
- Let α be the angle at point O between the vertical line and string OA.
- Using trigonometric ratios:
sinα=OBAB=513
cosα=OAAB=1213
5. Applying Equilibrium Conditions:
- Using the equilibrium condition for vertical forces:
T1sinα+T2sinα=13 kg
- For horizontal components:
T1cosα=T2cosα
6. Solving for Tensions:
- From the horizontal equilibrium:
T1⋅1213=T2⋅1213
- This implies T1=T2.
- Substituting into the vertical equilibrium:
T1⋅513+T2⋅1213=13
- Since T1=T2, let T1=T2=T:
T⋅513+T⋅1213=13
T⋅1713=13
T=13⋅1317=16917≈9.94 kg
7. Final Tensions:
- The tensions in the strings are:
- T1=5 kg
- T2=12 kg
Conclusion:
The correct option is (3) 5 kg and 12 kg.
- We have a body weighing 13 kg suspended by two strings of lengths 5 m and 12 m.
- The rod connecting the two strings is 13 m long, and the body hangs directly below the midpoint of the rod.
- Draw a triangle where:
- A and B are the ends of the rod (13 m apart).
- O is the point where the body is suspended.
- OA=12 m (length of the first string).
- OB=5 m (length of the second string).
- The triangle AOB is formed with AB=13 m.
- Since the body hangs directly below the midpoint, we can apply the Pythagorean theorem:
AB2=OA2+OB2
132=122+52
169=144+25
169=169
- This confirms that the triangle is a right triangle with ∠AOB=90∘.
- Let α be the angle at point O between the vertical line and string OA.
- Using trigonometric ratios:
sinα=OBAB=513
cosα=OAAB=1213
- Using the equilibrium condition for vertical forces:
T1sinα+T2sinα=13 kg
- For horizontal components:
T1cosα=T2cosα
- From the horizontal equilibrium:
T1⋅1213=T2⋅1213
- This implies T1=T2.
T1⋅513+T2⋅1213=13
- Since T1=T2, let T1=T2=T:
T⋅513+T⋅1213=13
T⋅1713=13
T=13⋅1317=16917≈9.94 kg
- The tensions in the strings are:
- T1=5 kg
- T2=12 kg
The correct option is (3) 5 kg and 12 kg.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A mass M of 100 kg is suspended with the use of strings A, B 90 and C as shown in the figure, where W is the vertical wall and R is a rigid horizontal rod. The tension in the string B is
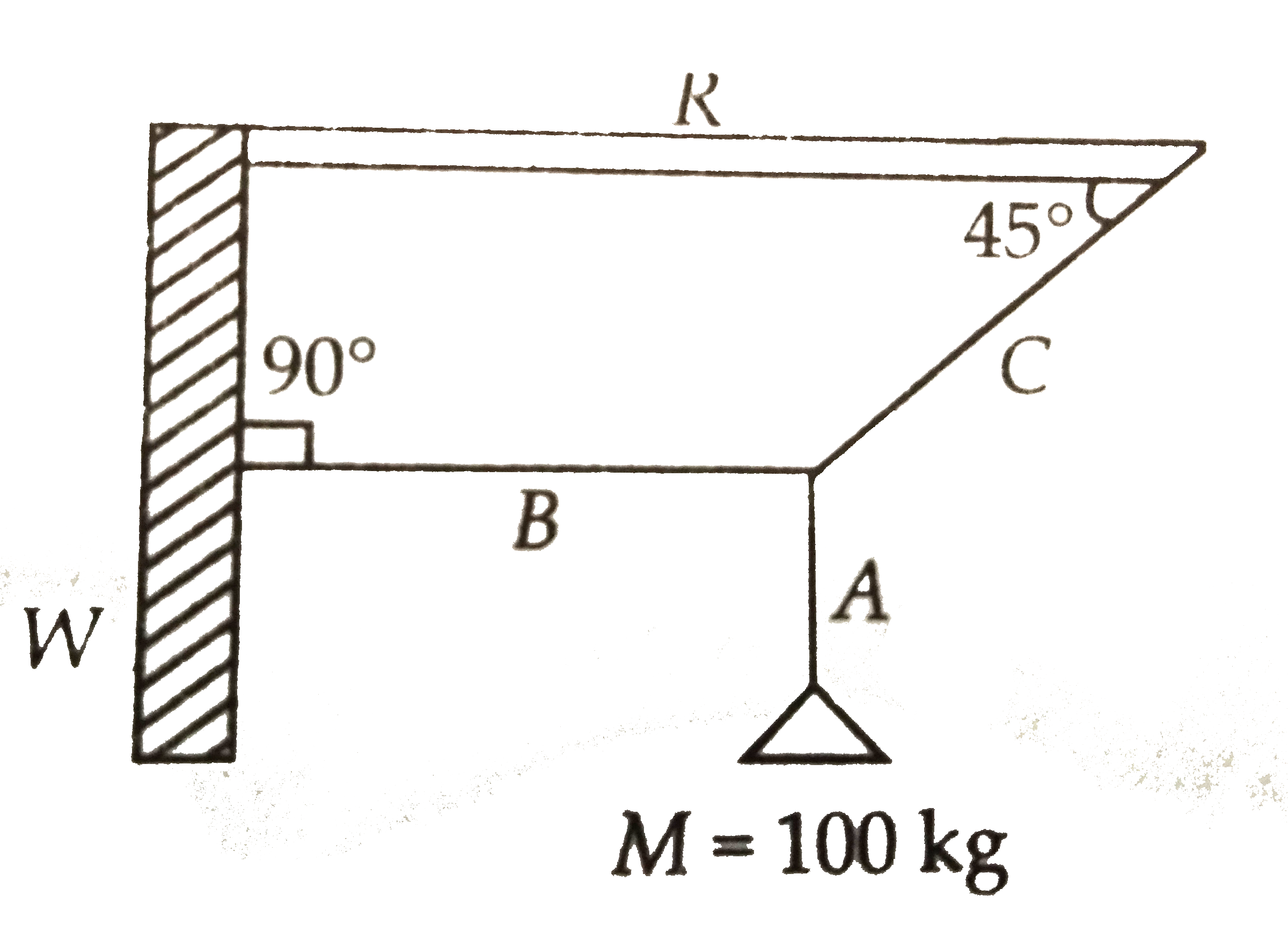 A100g NBzeroC100√2gND100√2gN
A100g NBzeroC100√2gND100√2gN
A uniform rod of mass 15kg is held stationary at 37 degree with the help of a light string as shown in Fig. The tension in the string is
 View Solution
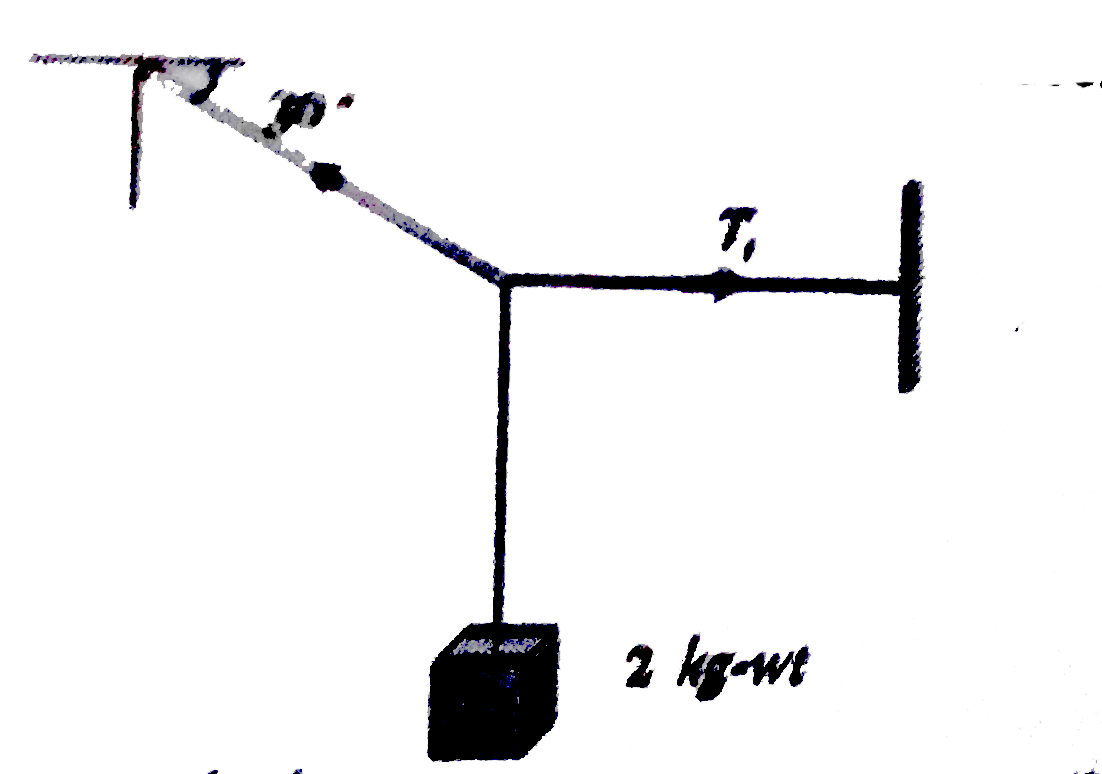
View SolutionA body of weight 2 kg is suspended as shown in the figure. The tension T2 in the horizontal string (in kg wt) is :-
View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
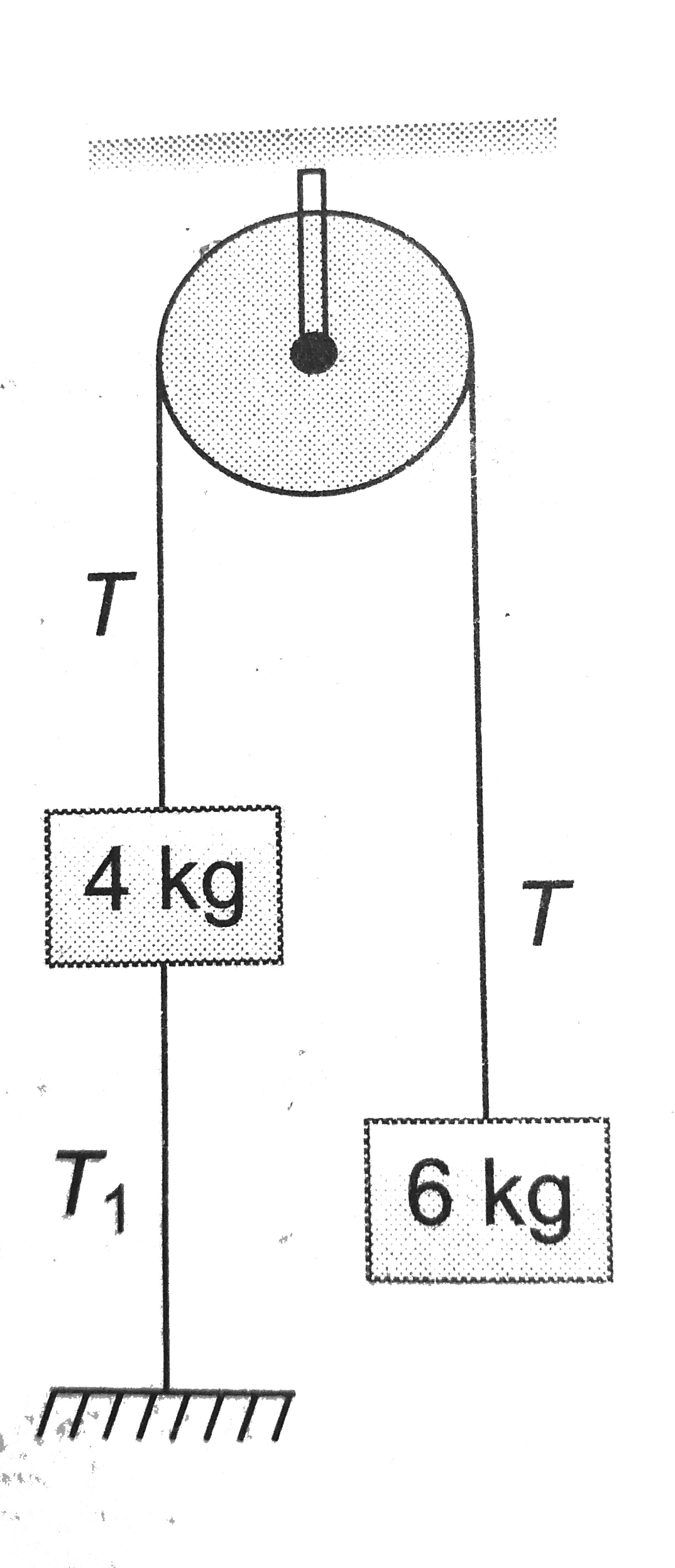
View SolutionTwo bodies of mass 4kg and 6kg are attached to the ends of a string passing over a pulley. The 4kg mass is attached to the table top by another string. The tension in this string T1 is equal to: Take
 View Solution
View SolutionA 2 kg stone at the end of a string 1 m long is whirled in a vertical circle. At some point its speed is 4m/s. The tension of the string is 51.6 newton. At this instant the stone is :
View SolutionA stone of mass 0.3kg attched to a 1.5m long stirng is whirled around in a horizontal cirlcle at a speed of 6 m/s The tension in the string is
View SolutionA body of mass 10 kg is suspended by a string and is pulled a side with a horizontal force of 49 N. Find the tension in the string, if the body is in equilibrium under these forces.
View Solution