A body of mass 10 kg is suspended by a string and is pulled a side with a horizontal force of 49 N. Find the tension in the string, if the body is in equilibrium under these forces.
To solve the problem of finding the tension in the string when a body of mass 10 kg is suspended and pulled aside with a horizontal force of 49 N, we can follow these steps:
Step 1: Calculate the weight of the body.
The weight (W) of the body can be calculated using the formula:
W=m⋅g
where:
- m=10kg (mass of the body)
- g=9.8m/s2 (acceleration due to gravity)
Calculating the weight:
W=10kg⋅9.8m/s2=98N
Step 2: Draw a free body diagram.
Draw a diagram representing the forces acting on the body:
- The weight (W) acting downwards (98 N).
- The horizontal force (F) acting sideways (49 N).
- The tension (T) in the string acting at an angle.
Step 3: Set up the equilibrium conditions.
Since the body is in equilibrium, the net force in both the horizontal and vertical directions must be zero.
In the vertical direction:
T⋅sin(θ)=W
In the horizontal direction:
T⋅cos(θ)=F
Step 4: Relate the angles using trigonometry.
From the free body diagram, we can express the angle θ in terms of the forces:
Using the tangent function:
tan(θ)=WF=9849=2
Thus, we can find θ using:
θ=tan−1(2)
Step 5: Calculate the tension using Pythagorean theorem.
To find the tension (T) in the string, we can use the Pythagorean theorem:
T=√W2+F2
Substituting the values:
T=√(98N)2+(49N)2
T=√9604+2401
T=√12005
T≈109.54N
Final Answer:
The tension in the string is approximately 109.54N.
---
The weight (W) of the body can be calculated using the formula:
W=m⋅g
where:
- m=10kg (mass of the body)
- g=9.8m/s2 (acceleration due to gravity)
W=10kg⋅9.8m/s2=98N
Draw a diagram representing the forces acting on the body:
- The weight (W) acting downwards (98 N).
- The horizontal force (F) acting sideways (49 N).
- The tension (T) in the string acting at an angle.
Since the body is in equilibrium, the net force in both the horizontal and vertical directions must be zero.
T⋅sin(θ)=W
In the horizontal direction:
T⋅cos(θ)=F
From the free body diagram, we can express the angle θ in terms of the forces:
Using the tangent function:
tan(θ)=WF=9849=2
Thus, we can find θ using:
θ=tan−1(2)
To find the tension (T) in the string, we can use the Pythagorean theorem:
T=√W2+F2
Substituting the values:
T=√(98N)2+(49N)2
T=√9604+2401
T=√12005
T≈109.54N
The tension in the string is approximately 109.54N.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS10videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - NUMERICAL EXXERCISE (LEVEL -1)13videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)5videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)10videos
GEOMETRICAL OPTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
Force of friction and tension in a string are
AGravitational forcesBElectromagnetic forcesCNuclear forcesDWeal forces
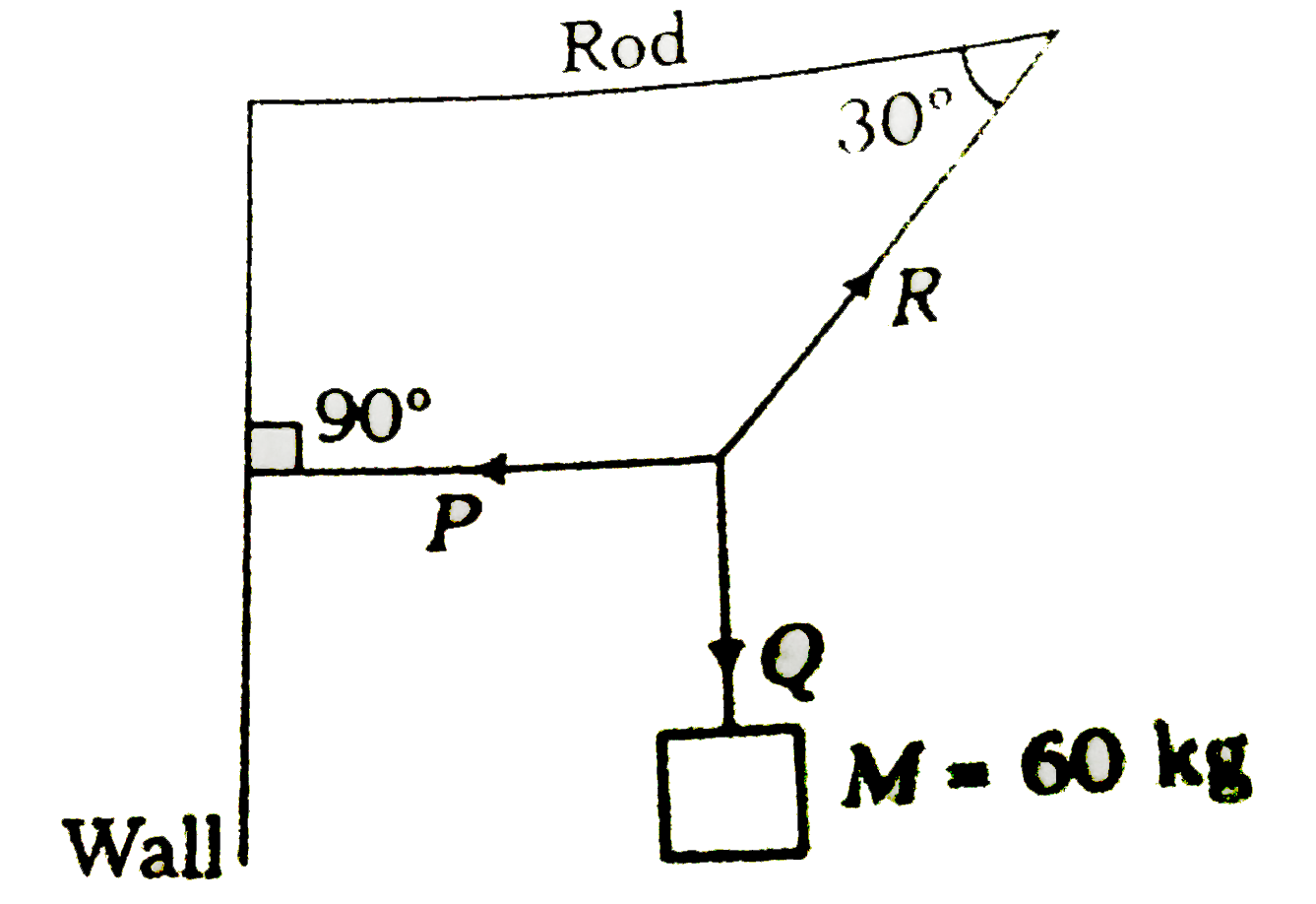
A body of mass 60 kg suspended by means of three strings, P, Q and R as shown in the figure is in equlibrium. The tension in the string P is
 View Solution
View SolutionA body of mass 60 kg suspended by means of three strings, P, Q and R as shown in the figure is in equlibrium. The tension in the string P is
 View Solution
View SolutionA body of mass 60 kg suspended by means of three strings, P, Q and R as shown in the figure is in equlibrium. The tension in the string P is
 View Solution
View SolutionA block of mass 10 kg is suspended by three strings as shown in figure . Tension T2 is
 View Solution
View SolutionA 10 kg body is suspended by a rope is pulled by means of a horizontal force to make 60° by rope to vertical. The horizontal force is
View SolutionA block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.
 View Solution
View SolutionA mass M kg is suspended by a weightless string. The horizontal force required to hold the mass at 60∘ with the vertical is
View Solution

