Two elastic wire A&B having length lA=2m and lB=1.5m have young's modules ratio YAYB=74. If rB=2mm then the radius of A given that due to application of the same force change in length in both A&B is same
1.7mm
1.9mm
2.7mm
2mm
The correct Answer is:A
To solve the problem, we will use the relationship between Young's modulus, force, length, area, and change in length. Let's go through the solution step by step.
1. Understanding Young's Modulus:
The formula for Young's modulus Y is given by:
Y=F⋅LA⋅ΔL
where:
- F is the applied force,
- L is the original length of the wire,
- A is the cross-sectional area,
- ΔL is the change in length.
2. Setting Up the Equations:
For wire A:
YA=F⋅LAπr2A⋅ΔL
For wire B:
YB=F⋅LBπr2B⋅ΔL
3. Taking the Ratio of Young's Moduli:
Given the ratio of Young's moduli:
YAYB=74
Substituting the expressions for YA and YB:
F⋅LAπr2A⋅ΔLF⋅LBπr2B⋅ΔL=74
4. Simplifying the Ratio:
Canceling out common terms F, π, and ΔL:
LA⋅r2BLB⋅r2A=74
5. Substituting Known Values:
We know:
- LA=2m
- LB=1.5m
- rB=2mm=0.002m
Substitute these values into the equation:
2⋅(0.002)21.5⋅r2A=74
6. Cross-Multiplying:
Cross-multiplying gives:
8⋅(0.002)2=7⋅1.5⋅r2A
7. Calculating:
Calculate 8⋅(0.002)2:
8⋅(0.000004)=0.000032
And 7⋅1.5=10.5:
0.000032=10.5⋅r2A
8. Solving for r2A:
Rearranging gives:
r2A=0.00003210.5
Calculating r2A:
r2A=0.00000304761905
9. Finding rA:
Taking the square root:
rA=√0.00000304761905≈0.001743m=1.743mm
10. Final Answer:
Rounding to two decimal places, the radius of wire A is approximately:
rA≈1.74mm
The formula for Young's modulus Y is given by:
Y=F⋅LA⋅ΔL
where:
- F is the applied force,
- L is the original length of the wire,
- A is the cross-sectional area,
- ΔL is the change in length.
For wire A:
YA=F⋅LAπr2A⋅ΔL
For wire B:
YB=F⋅LBπr2B⋅ΔL
Given the ratio of Young's moduli:
YAYB=74
Substituting the expressions for YA and YB:
F⋅LAπr2A⋅ΔLF⋅LBπr2B⋅ΔL=74
Canceling out common terms F, π, and ΔL:
LA⋅r2BLB⋅r2A=74
We know:
- LA=2m
- LB=1.5m
- rB=2mm=0.002m
2⋅(0.002)21.5⋅r2A=74
Cross-multiplying gives:
8⋅(0.002)2=7⋅1.5⋅r2A
Calculate 8⋅(0.002)2:
8⋅(0.000004)=0.000032
And 7⋅1.5=10.5:
0.000032=10.5⋅r2A
Rearranging gives:
r2A=0.00003210.5
Calculating r2A:
r2A=0.00000304761905
Taking the square root:
rA=√0.00000304761905≈0.001743m=1.743mm
Rounding to two decimal places, the radius of wire A is approximately:
rA≈1.74mm
Topper's Solved these Questions
Similar Questions
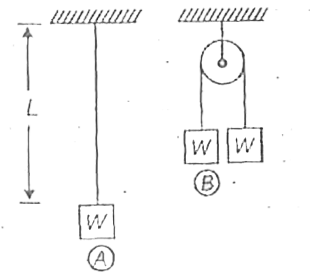
If in case A, elongation in wire of length L is l then for same wire elongation in case B will be
 View Solution
View SolutionTwo wires A and B have the same length and area of cross-secton. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
View Solution
Knowledge Check
- Question 1 - Select One
Two wires A and B are of the same maeterial. Their lengths are in the ratio 1 : 2 and the diameters are in the ratio 2 : 1. IF they are pulled by the same force, their increases in length will be in the ratio
A2:1B1:4C1:8D8:1 - Question 2 - Select One
Two planets A and B have the same material density. If the radius of A is twice that of B, then the ratio of the escape velocity VA/VB is
A2B√2C1/√2D1/2
Two wires A and B of same material have radii in the ratio 2:1 and lengths in the ratio 4:1. The ratio of the normal forces required to produce the same change in the lengths of these two wires is
View SolutionYoung's moduli of two wires A and B are in the ratio 7:4 wire A is 2m long and has radius R. . wire B is 1.5mlong has radius 2mm for a given load , then the value of R is close to:
View SolutionEnds of two wires A and B, having resistivityρA=3×105Ωm and ρB=6×10−5ωm of same cross section ara are pointed together to form a single wire. If the resistance of the joined wire does not change with temperature, then find the ratio of their lengths given that temperatue coefficient of resistitivy of wires A and B are α=4×10−5/∘C and α=−4×106/∘C . Assume that mechanical dimensions do not change with temperature.
View SolutionTwo wire A and B of length l, radius r and length 2l, radius 2r having same Young's modulus Y are hung with a width mg, fig. What is the net elongation in the two wires?
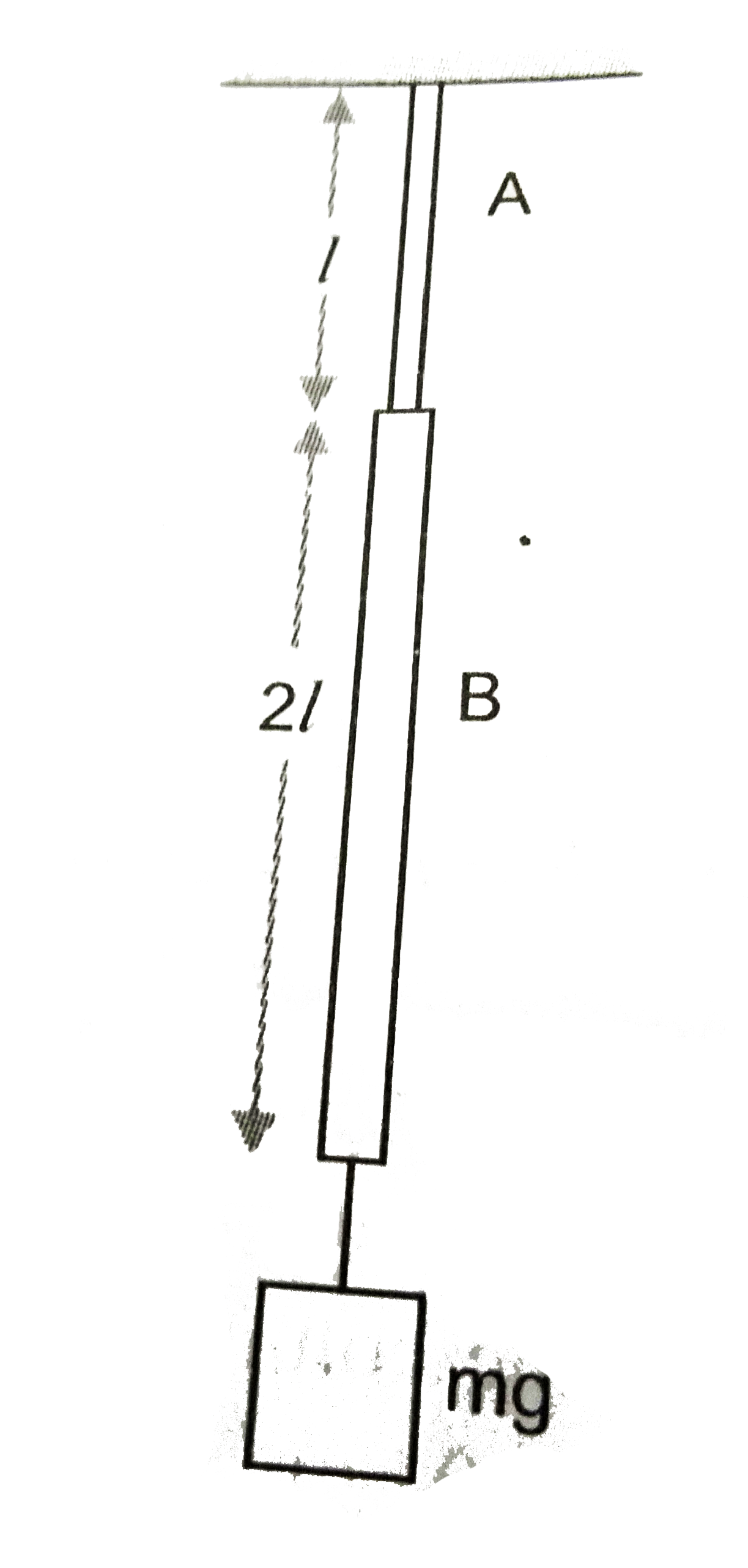 View Solution
View SolutionA force F is required to break a wire of length L and radius r. Find the force required to break a wire of the same material, length 2L and radius 4r.
View SolutionA wire of given metarial having length l and ares of cross-section A has a resistance of 4Ω. What would be the resistance of another wire of the same meterial having length l/2 and area of cross-section 2A ?
View Solution

