Young's moduli of two wires A and B are in the ratio 7:4 wire A is 2m long and has radius R. . wire B is 1.5mlong has radius 2mm for a given load , then the value of R is close to:
1.85mm
1.9mm
1.7mm
1.3mm
The correct Answer is:B
To solve the problem, we will use the relationship between Young's modulus, length, area, and the given ratio of Young's moduli for the two wires.
1. Understanding Young's Modulus:
The Young's modulus (Y) is defined as:
Y=F/AΔL/L
where F is the force applied, A is the cross-sectional area, ΔL is the change in length, and L is the original length.
2. Given Data:
- Young's moduli ratio: YAYB=74
- Length of wire A: LA=2m
- Length of wire B: LB=1.5m
- Radius of wire B: rB=2mm=0.002m
3. Cross-sectional Areas:
- Area of wire A: AA=πR2
- Area of wire B: AB=π(0.002)2=π×0.000004m2
4. Equating Young's Modulus for Both Wires:
Since the load (force) is the same for both wires, we can set up the equation:
YA⋅AALA=YB⋅ABLB
5. Substituting the Known Values:
Substitute the areas and the ratio of Young's moduli:
7⋅πR22=4⋅π×0.0000041.5
6. Canceling π:
The π cancels out from both sides:
7R22=4×0.0000041.5
7. Calculating the Right Side:
Calculate the right side:
4×0.0000041.5=0.0000161.5≈0.00001067
8. Setting Up the Equation:
Now we have:
7R2=2×0.00001067
7R2=0.00002134
9. Solving for R2:
R2=0.000021347≈0.000003052
10. Finding R:
R≈√0.000003052≈0.00174m=1.74mm
Final Answer:
The value of R is approximately 1.74 mm.
The Young's modulus (Y) is defined as:
Y=F/AΔL/L
where F is the force applied, A is the cross-sectional area, ΔL is the change in length, and L is the original length.
- Young's moduli ratio: YAYB=74
- Length of wire A: LA=2m
- Length of wire B: LB=1.5m
- Radius of wire B: rB=2mm=0.002m
- Area of wire A: AA=πR2
- Area of wire B: AB=π(0.002)2=π×0.000004m2
Since the load (force) is the same for both wires, we can set up the equation:
YA⋅AALA=YB⋅ABLB
Substitute the areas and the ratio of Young's moduli:
7⋅πR22=4⋅π×0.0000041.5
The π cancels out from both sides:
7R22=4×0.0000041.5
Calculate the right side:
4×0.0000041.5=0.0000161.5≈0.00001067
Now we have:
7R2=2×0.00001067
7R2=0.00002134
R2=0.000021347≈0.000003052
R≈√0.000003052≈0.00174m=1.74mm
The value of R is approximately 1.74 mm.
Topper's Solved these Questions
Similar Questions
Two wires A and B are made of same material. The wire A has a length l and diameter r while the wire B has a length 2l and diameter r/2. If the two wires are stretched by the same force the elongation in A divided by the elongation in B is
View SolutionTwo wires A & B bend like as shown in figure. 'A' has radius 2 cm and current 1A wire B has radius 4cm & current 3A then ratio of magnetic field
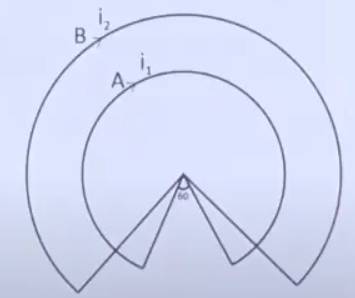
View Solution
Knowledge Check
The radii and Young's moduli of two uniform wires A and B are in the ratio 2:1 and 1:2 respectively. Both wires are subjected to the same longitudinal force. If the increase in length of the wire A is one percent, the percentage increase in length of the wire B is
A1.0B1.5C2.0D3.0The young's modulus of a wire of length (L) and radius (r ) is Y. If the length is reduced toL2 and radius r2 , then its young's modulus will be
AY2BYC2YD4Y
The young's modulus of a wire of length (L) and radius (r ) is Y. If the length is reduced toL2 and radius r2 , then its young's modulus will be
View SolutionThe young's modulus of a wire of length (L) and radius (r ) is Y. If the length is reduced toL2 and radius r2 , then its young's modulus will be
View SolutionTwo identical wires AandB , each of length 'l', carry the same current I. Wire A is bent into a circle of radius RandwireB is bent to form a square of side 'a' . If BAandBB are the values of magnetic field at the centres of the circle and square respectively , then the ratio BABB is :
View SolutionTwo identical wires AandB , each of length 'l', carry the same current I. Wire A is bent into a circle of radius RandwireB is bent to form a square of side 'a' . If BAandBB are the values of magnetic field at the centres of the circle and square respectively , then the ratio BABB is :
View SolutionA long straight wire is placed along the axis of a circuit ring of radius R. The mutual inductance of this system is
View SolutionA current of 2 amp. flows in a long, straight wire of radius 2mm. The intensity of magnetic field on the axis of the wire is
View Solution
