A block of mass 500g and specific heat 400J/KgK is attached with a spring of spring constant 800N/m. Now block is dipped in water of mass 1kg and specific heat 4184J/KgK. Now the spring is elongated by 2cm and released. Find rise in temperature of water and block system when block finally comes to rest.
7.64×10−4K
3.64×10−3K
3.64×10−5K
3.64×10−6K
The correct Answer is:C
To solve the problem, we need to calculate the rise in temperature of the water and block system when the block comes to rest after being released from the elongated spring. Here are the steps to find the solution:
Step 1: Understand the Energy Conversion
When the block is released, the potential energy stored in the spring will be converted into heat energy, which will raise the temperature of both the block and the water.
Step 2: Calculate the Potential Energy of the Spring
The potential energy (PE) stored in the spring when it is elongated can be calculated using the formula:
PE=12ka2
where:
- k=800N/m (spring constant)
- a=0.02m (elongation)
Substituting the values:
PE=12×800×(0.02)2=12×800×0.0004=0.16J
Step 3: Set Up the Heat Energy Equation
The heat energy gained by the block and water when the block comes to rest is given by:
Q=m1s1ΔT+m2s2ΔT
where:
- m1=0.5kg (mass of the block)
- s1=400J/(kg K) (specific heat of the block)
- m2=1kg (mass of the water)
- s2=4184J/(kg K) (specific heat of the water)
- ΔT is the rise in temperature (which we need to find)
Step 4: Substitute Values into the Heat Energy Equation
Now we can substitute the values into the equation:
0.16=(0.5×400ΔT)+(1×4184ΔT)
This simplifies to:
0.16=(200ΔT)+(4184ΔT)
0.16=(200+4184)ΔT
0.16=4384ΔT
Step 5: Solve for ΔT
Now, we can solve for ΔT:
ΔT=0.164384
Calculating this gives:
ΔT≈3.64×10−5K
Final Answer
The rise in temperature of the water and block system when the block finally comes to rest is approximately:
ΔT≈3.64×10−5K
When the block is released, the potential energy stored in the spring will be converted into heat energy, which will raise the temperature of both the block and the water.
The potential energy (PE) stored in the spring when it is elongated can be calculated using the formula:
PE=12ka2
where:
- k=800N/m (spring constant)
- a=0.02m (elongation)
PE=12×800×(0.02)2=12×800×0.0004=0.16J
The heat energy gained by the block and water when the block comes to rest is given by:
Q=m1s1ΔT+m2s2ΔT
where:
- m1=0.5kg (mass of the block)
- s1=400J/(kg K) (specific heat of the block)
- m2=1kg (mass of the water)
- s2=4184J/(kg K) (specific heat of the water)
- ΔT is the rise in temperature (which we need to find)
Now we can substitute the values into the equation:
0.16=(0.5×400ΔT)+(1×4184ΔT)
This simplifies to:
0.16=(200ΔT)+(4184ΔT)
0.16=(200+4184)ΔT
0.16=4384ΔT
Now, we can solve for ΔT:
ΔT=0.164384
Calculating this gives:
ΔT≈3.64×10−5K
The rise in temperature of the water and block system when the block finally comes to rest is approximately:
ΔT≈3.64×10−5K
Topper's Solved these Questions
Similar Questions
A block of mass 0.1 kg attached to a spring of spring constant 400 N/m is putted rightward from x0=0 to x1=15 mm. Find the work done by spring force.
View Solutiona block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural lengthView Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beView SolutionA block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
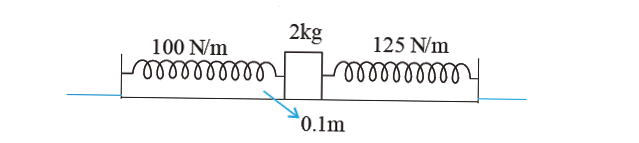
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.View SolutionA block of mass 0.18kg is attached to a spring of force-constant 2N/m. The coefficient of friction between the block and the floor is 0.1 Initially the block is at rest and the spring is un-stretched. An impulse is given to the block as shown in the figure. The block slides a distance of 0.06m and comes to rest for the first time. The initial velocity of the block in m//s is V=N/10. Then N is :
 .View Solution
.View SolutionA block of 2 kg is suspended from the ceiling through a massless spring of spring constant k=100 N/m. What is the elongation of the spring? If another 1 kg is added to the block, what would be the further elongation?
View SolutionA block of mass 100g attached to a spring of stiffness 100N/m is lying on a frictionless floor as shown. The block is moved to compress the spring by 10cm and released. If the collision with the wall is elastic then find the time period of oscillations.
 View Solution
View Solution

