a block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
2⋅10−2J
2⋅10−6J
3⋅10−6J
4⋅10−2J
The correct Answer is:A
To solve the problem of finding the work done by the spring force when a block of mass 0.1 kg is attached to a spring with a spring constant of 400 N/m and is pulled from x = 0 to x1 = 10 mm, we can follow these steps:
1. Understand the Problem:
We have a spring with a spring constant k=400N/m that is stretched from an initial position x=0 to a final position x1=10mm.
2. Convert Units:
Convert the displacement from millimeters to meters, since the spring constant is in N/m.
x1=10mm=10×10−3m=0.01m
3. Use the Formula for Work Done by Spring Force:
The work done by the spring force when it is stretched or compressed is given by:
W=−12kx2
where W is the work done, k is the spring constant, and x is the displacement from the equilibrium position.
4. Substitute the Values:
Substitute k=400N/m and x=0.01m into the formula:
W=−12×400×(0.01)2
5. Calculate (0.01)2:
(0.01)2=0.0001m2
6. Calculate the Work Done:
Now substitute (0.01)2 back into the equation:
W=−12×400×0.0001
W=−4002×0.0001=−200×0.0001=−0.02J
7. Final Result:
The work done by the spring force is:
W=−0.02J=−2×10−2J
Conclusion:
The work done by the spring force when the block is pulled from x=0 to x1=10mm is −2×10−2J.
We have a spring with a spring constant k=400N/m that is stretched from an initial position x=0 to a final position x1=10mm.
Convert the displacement from millimeters to meters, since the spring constant is in N/m.
x1=10mm=10×10−3m=0.01m
The work done by the spring force when it is stretched or compressed is given by:
W=−12kx2
where W is the work done, k is the spring constant, and x is the displacement from the equilibrium position.
Substitute k=400N/m and x=0.01m into the formula:
W=−12×400×(0.01)2
(0.01)2=0.0001m2
Now substitute (0.01)2 back into the equation:
W=−12×400×0.0001
W=−4002×0.0001=−200×0.0001=−0.02J
The work done by the spring force is:
W=−0.02J=−2×10−2J
The work done by the spring force when the block is pulled from x=0 to x1=10mm is −2×10−2J.
Topper's Solved these Questions
Similar Questions
A block of mass 0.1 kg attached to a spring of spring constant 400 N/m is putted rightward from x0=0 to x1=15 mm. Find the work done by spring force.
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural length
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA spring of spring constasnt 50 N/m is compressed from its natural position through 1 cm. Find the work done by the work done by the spring force on the agency compressing the spring.
View SolutionA small block of mass 2 kg is placed on a bigger block of mass 4 kg which is attached to horizontal spring of spring constant K=500N/m as shown in figure, coefficient of friction between block is 0.2 .Maximum amplitude of system so that there is no relative slipping between blocks.
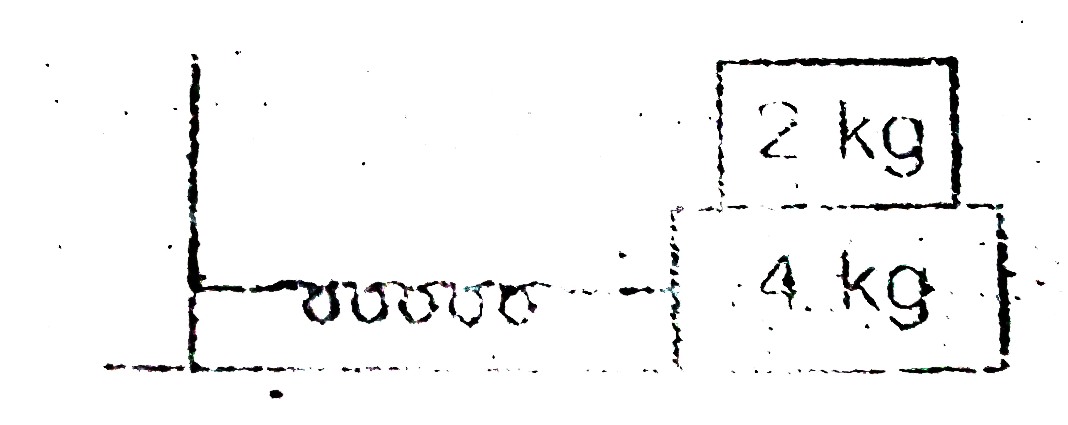
View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionA block of mass 0.01 kg is attached to a spring of force constant 10−1Nm−1 . If the energy of oscillation is 10−5 J, find the angular frequency and amplitude of oscillation.
View SolutionOne end of a fixed spring is pulled by an average force of 10N through a distance of 5cm, find the work done by the spring.
View SolutionA block whose mass is 2 kg is fastened on a spring whose spring constant is 100 Nm−1 . It is pulled to a distance of 0.1 m from over a frictionless surface and is released at t=0. Calculate the kinetic eneryg of the block when it is 0.05 m away from its mean position.
View Solution
